4. Геометрическая вероятность

Рассмотрим n-мерное вещественное пространство . Пусть в какую-то ограниченную область наудачу брошена точка. Слово «наудачу» означает, что все точки области равновозможны. В этом случае вероятность попадания точки в какую-то подобласть определяется формулой

, (1.2)

где – меры множеств A и  соответственно. Мерой m(A) множества A называется его длина l, если ; его площадь S, если 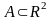и его объём V, если 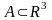. В общем случае, если , то мерой множества называют его n-мерный объём. Элементарными исходами называются точки множества  (которое играет роль пространства элементарных исходов), а благоприятствующими исходами – точки множества A.

Пример 1.8. (Задача о встрече) Два лица A и B условились встретиться в определённом месте между 12 и 13 часами. Пришедший первым ждёт другого в течение 20 мин, после чего уходит. Чему равна вероятность встречи лиц A и B, если приход каждого из них может произойти наудачу в течение указанного часа, и моменты прихода независимы?

Р ешение. Обозначим моменты прихода лица A через x, а лица B через y. Для того, чтобы встреча произошла, необходимо и достаточно, чтобы . Представим x и y как координаты на плоскости, а в качестве единицы масштаба выберем минуту. Всевозможные исходы представляются точками квадрата со стороной 60, а благоприятствующие встрече – располагаются в заштрихованной области.

Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата:

Пример 1.9. Точка брошена наудачу на отрезок [1;3]. Какова вероятность попадания точки в интервал (1,5;2,6)?

Решение. Здесь пространство элементарных исходов весь отрезок =[1;3], а множество благоприятствующих исходов A=(1,5;2,6), при этом длины этих интервалов равны l()=2 и l(A)=1,1. Поэтому вероятность попадания брошенной точки в указанный интервал равна

Пример 1.10. На отрезок [0;2] брошены наудачу поочерёдно две точки. Какова вероятность, что первая точка лежит правее второй точки?

Р ешение. Обозначим координаты точек через x и y. Элементарным исходом при таком бросании будет пара (x,y), а пространством элементарных исходов – квадрат . Событие A={первая точка лежит правее второй} равносильно условию , тогда , т.е. представляет собой треугольник (рисунок 1.2). Площади квадрата и треугольника соответственно равны и , поэтому вероятность

16. Два лица условились встретиться в определенном месте между 18 и 19 часами и договорились, что пришедший первым ожидает второго в течение 15 мин., после чего уходит. Найти вероятность их встречи, если приход каждого в течение указанного времени может произойти в любое время, и моменты прихода независимы. (0,4375)

17. Какова вероятность, что наудачу брошенная в круг точка окажется внутри вписанного в круг квадрата? (2/0,637)

18. В шар вписан куб. Какова вероятность, что выбранная наугад внутри шара точка окажется внутри квадрата? (1,48)

19. Наугад названы два положительных числа, каждое из которых не превосходит единицы. Какова вероятность, что их сумма больше единицы, а произведение не более 0,5? (0,35)

20. Наугад названы два положительных числа x и y, каждое из которых не превосходит двух. Какова вероятность, что произведение xy не больше единицы, а частное y/x не более двух? (0,38)