9. Показательный закон распределения

Определение. Показательным (экспоненциальным) называют распределение вероятностей случайной величины которое описывается плотностью

Здесь параметр

Функция распределения показательного закона

.

Тогда в окончательном виде

Графики плотности и функции распределения при изображены на рисунке 3.6.

Рисунок 3.6.

Вероятность попадания показательно распределенной случайной величины в интервал определяется формулой

.

Определим числовые характеристики показательного закона распределения – математическое ожидание и дисперсию.

.

. .

Итак, .

Пример 3.22. Время расформирования состава через горку – случайная величина, подчиненная показательному закону. Пусть – среднее число поездов, которые горка может расформировать за 1 час. Определить вероятность того, что время расформирования состава: 1) меньше 30 мин; 2) больше 6 мин, но меньше 24 мин.

Решение.1)Вероятность того, что время расформирования состава займёт менее 30 мин = 0,5 ч, есть

1. Вероятность того, что время расформирования состава займет от 6 мин = 0,1 ч до 24 мин = 0,4 ч:

Функция надёжности

Элементом называют некоторое устройство, независимо от того, «простое» оно или «сложное». Пусть элемент начинает работать в момент времени , а в момент t происходит отказ. Обозначим через T непрерывную случайную величину – длительность времени безотказной работы элемента, а через – интенсивность отказов (среднее число отказов в единицу времени).

Часто длительность времени безотказной работы элемента имеет показательное распределение с функцией распределения

,

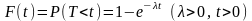которая определяет вероятность отказа элемента за время длительностью t.

Определение. Функцией надёжности называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t:

.

Пример 3.23. Длительность времени безотказной работы элемента имеет показательное распределение . Найти вероятность того, что за время длительностью 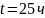: а) элемент откажет; б) элемент не откажет.

Решение. а) Так как функция распределения определяет вероятность отказа элемента за время длительностью то вероятность отказа:

;

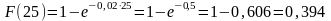б) события «элемент откажет» и «элемент не откажет» – противоположные, поэтому вероятность того, что элемент не откажет

.

Этот же результат можно получить непосредственно, пользуясь функцией надёжности , определяющей вероятность безотказной работы элемента за время длительностью :

.◄

Важнейшее свойство показательного распределения, отличающее его ото всех других распределений, состоит в следующем: если промежуток времени, распределённый по показательному закону, уже длился некоторое время  то это никак не влияет на закон распределения оставшейся части промежутка T-: он будет таким же, как и закон распределения всего промежутка T.

Вопросы для повторения

1. Что называется случайной величиной? Приведите примеры дискретных и непрерывных случайных величин.

2. Что такое функция распределения F(x) случайной величины X?

3. Перечислите свойства функции распределения.

4. Ряд распределения и функция распределения дискретной случайной величины.

5. Дайте определение математического ожидания дискретной случайной величины и перечислите его свойства.

6. Что такое дисперсия случайной величины? Перечислите свойства дисперсии. Что такое среднее квадратичное отклонение?

7. Про какую величину говорят, что она имеет гипергеометрическое распределение?

8. Дайте описание схемы Бернулли независимых повторных испытаний. Запишите формулу Бернулли.

9. Что такое наивероятнейшее число испытаний в схеме Бернулли? Как его можно найти?

10. Дайте определение биномиального закона распределения. Как вычисляются его числовые характеристики?

11. Какая случайная величина называется непрерывной?

12. Перечислите свойства плотности распределения вероятностей.

13. Запишите формулы для вычисления математического ожидания и дисперсии непрерывной случайной величины заданной на отрезке .

14. В каких ситуациях применяется равномерный закон распределения?

15. Дайте определение нормального закона распределения с параметрами a и . Нарисуйте график плотности нормального распределения с параметрами .

16. В чём заключается «правило трёх сигм»?

17. Задаёт ли данная таблица закон распределения некоторой случайной величины? Обоснуёте свой ответ.

	–2	0	1	4	6	8
	0,2	0,05	0,3	0,1	0,05	0,2