6. Равномерный закон распределе ния

Определение: Непрерывная случайная величина имеет равномерный закон распределения на отрезке если ее плотность распределения 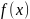постоянна на этом отрезке и равна нулю вне этого отрезка:

(3.12)

Графики плотности и функции распределения сл.в. приведены на рисунке 3.4.

Рисунок 3.4

Функция распределения равномерной случайной величины имеет вид:

(3.13)

ее математическое ожидание и дисперсия

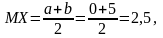
(3.14)

Равномерный закон распределения применяется при анализе ошибок округления, при проведении числовых расчетов, в ряде задач массового обслуживания.

Так, случайная величина равномерно распределенная на отрезке [0;1] и называемая «случайным числом от 0 до 1», служит исходным материалом для получения случайных величин с любым законом распределения.

Пример 3.18. Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты. Найти математическое ожидание и среднее квадратическое отклонение случайной величины времени ожидания поезда.

Решение. Сл. в. время ожидания поезда – распределена равномерно на отрезке [0;2] с плотностью 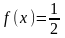при . Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна:

Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:

мин, мин.

14. Автобус некоторого маршрута идет строго по расписанию с интервалом 5 мин. Сл.в. X – время ожидания автобуса пассажиром. Найти: а) функцию F(x) и плотность f(x) распределения; б) в) вероятность того, что пассажир, подошедший к остановке, будет ожидать не более двух мин. ( )

15. Цена деления шкалы амперметра равна 0,1 А. Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

(P(0,02<X<0,08)= 0,5.)

16. Случайная величина X распределена равномерно в интервале (5;11). Найти вероятность попадания в интервал .

7. Нормальный закон распределения

Нормальный закон распределения наиболее часто встречается на практике. Главная его особенность состоит в том, что он является предельным законом, к которому приближаются другие законы при весьма часто встречающихся типичных условиях.

Определение: Непрерывная случайная величина имеет нормальный закон распределения (закон Гаусса) с параметрам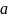и и , если плотность распределения имеет вид

(3.15)

где

Кривую нормального закона распределения называют нормальной кривой или кривой Гаусса. Графики плотности и функции распределения нормального закона с параметрами , приведены на рисунке 3.5.

Рисунок 3.5

Свойства нормального распределения

1. Вероятность попадания нормальной случайной величины в интервал равна

(3.16)

где функция Лапласа, ее значения приведены в приложении III. Так как , то функция распределения случайной величины распределённой по нормальному закону, определяется формулой:

. (3.17)

2. Вероятность того, что отклонение нормальной случайной величины от своего математического ожидания не превысит величину (по абсолютной величине), равна

(3.18)

Найдем вероятности отклонения нормальной случайной величины от математического ожидания на величину Значения функции Лапласа находим в приложении III.

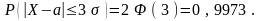
Отсюда вытекает «Правило трех сигм»:

С вероятностью, практически равной единице, значения нормальной случайной величины попадают в интервал

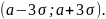
Пример 3.19. Производится измерение без систематических ошибок диаметра вала. Случайная ошибка измерения X подчиняется нормальному закону распределения со средним квадратическим отклонением 20мм. Найти: а) вероятность того, что измерение будет произведено с ошибкой, по абсолютной величине не превосходящей 35 мм; б) интервал, в который попадет сл.в. X с вероятностью 0,6827.

Решение. Ошибка измерения это случайная величина. Так как по условию систематическая ошибка отсутствует, то

_а) По формуле 3.18

б)

Пример 3.20. Случайная величина распределена нормально с математическим ожиданием . Вероятность попадания в интервал (10;20) равна 0,3. Найти вероятность попадания в интервал (0;10).

Решение. Так как нормальная кривая симметрична относительно кривой то площади, ограниченные сверху нормальной кривой и снизу – интервалами (0;10) и (10;20), равны между собой. Поскольку эти площади численно равны вероятностям попадания в соответствующий интервал, то

Пример 3.21. Полагая, что рост мужчин определённой возрастной группы есть нормально распределённая случайная величина 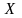с параметрами , найти:

1. а) выражение плотности вероятности и функции распределения случайной величины ; б) долю костюмов 4-го роста (176 – 182 см ), которую нужно предусмотреть в общем объёме производства для данной возрастной группы.

2. Найти рост x мужчин данной возрастной из условия . Объяснить смысл полученного значения.

3. Сформулировать правило «трёх сигм» для случайной величины .

Решение.1. а) По формулам (3.15) и (3.17) запишем

, .

б) Доля костюмов 4-го сорта в общем объёме производства определяется по формуле (3.16) как вероятность

Здесь .

2. .

По таблице III приложений найдём и

.

Это означает, что 70% мужчин данной возрастной группы имеют рост до 176 см.

3. Практически достоверно, что рост мужчин данной возрастной группы заключён в границах от 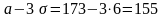до (см), т.е. (см).

В силу особенностей нормального закона распределения, отмеченных в начале параграфа, он занимает центральное место в теории и практике вероятностно-статистических методов.

17. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равной 50 мм. Фактическая длина изготовленных деталей не менее 32 мм и не более 68 мм. Деталь считается годной, если отклонение её длины от проектной не превышает . Сколько процентов годных деталей штампует автомат?

18. Случайная величина X распределена нормально с параметрами Найти интервал, в котором с вероятностью 0,9973 будут заключены значения сл.в. X.