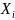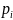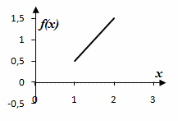4. Биномиальное распределение вероятностей

Говорят, что дискретная случайная величина Х, принимающая значения 0, 1, 2, …, k, …, n с вероятностями, которые находятся по формуле Бернулли, имеет биномиальный закон распределения с параметрами n и p.

Пример 3.10. В портфеле компании 3 краткосрочных инвестиционных проекта. Вероятность получения прибыли в первый год работы проекта равна 0,7. Найти распределение случайной величины X – числа проектов, по которым получена прибыль в первый год работы.

Решение. Применим формулу Бернулли.

Запишем распределение случайной величины X в таблицу:

X	0	1	2	3
p	0,027	0,189	0,441	0,343

Найдём математическое ожидание и дисперсию биномиально распределённой случайной величины. Пусть – число наступлений события A в i-том испытании, тогда 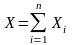, где имеет следующий закон распределения:

	0	1
	q	p

Находим математическое ожидание X:

.

Из независимости испытаний следует независимость , поэтому

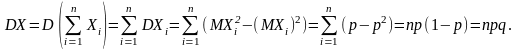
Таким образом, числовые характеристики биномиального закона

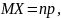(3.9)

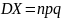, (3.10)

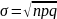. (3.11)

Пример 3.11. Вероятность выигрыша по облигации займа за все время его действия равна 0,1. Некто приобрёл 30 облигаций. Найти математическое ожидание и дисперсию случайной величины – числа выигравших облигаций среди 30 приобретенных.

Решение. Сл.в. биномиально распределена с параметрами Тогда

Остановимся на происхождении названия «биномиальное распределение». Алгебраическое выражение , где n – натуральное число, называется биномом Ньютона n-й степени. Из школьного курса математики известны биномы Ньютона второй и третьей степени:

;

.

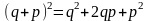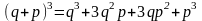В общем случае бином Ньютона описывается формулой:

.

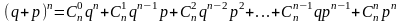В соответствии с формулой Бернулли (2.1) заключаем, что

.

Таким образом, вероятности 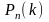совпадают с членами разложения бинома Ньютона. Отсюда и происходит название «биномиальное распределение».

Так как для вероятностей q и p верно соотношение , то и 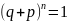, т.е. сумма вероятностей биномиального распределения равна единице: . Значит, распределение определено корректно.

8. Отрезок AB длины 15 см разделён точкой C в отношении 2:1. На этот отрезок наудачу брошены 4 точки. Найти вероятность того, что две из них попали левее точки С, а две – правее. (8/27)

9. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти математическое ожидание и дисперсию сл.в. X – числа книг без брака.

10. Устройство состоит из трёх независимо работающих элементов. Вероятность отказа каждого элемента 0,1. Составить закон распределения сл.в. X – числа отказавших элементов. Найти ( )

4. Непрерывные случайные величины

Определение. Случайная величина называется непрерывной, если её функция распределения имеет вид

где 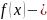некоторая неотрицательная функция, называемая плотностью распределения вероятностей данной случайной величины.

Теорема. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю.

Доказательство. Покажем, что для любого значения случайной величины вероятность

Следствие. Если – непрерывная случайная величина, то вероятность попадания в интервал не зависит от того, является этот интервал открытым или закрытым, т.е.

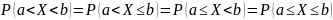
Непрерывная случайная величина может принять любое значение из некоторого интервала в отличие от дискретной случайной величины, которая, как указывалось выше, может принимать только отдельные изолированные значения.

Плотность распределения вероятностей обладает следующими свойствами:

1. 

2. 

3. 

4. если в точке функция 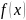непрерывна, то

Математическое ожидание и дисперсия непрерывной случайной величины определяются формулами:

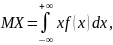
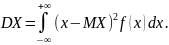
Формула для вычисления дисперсии:

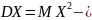
где

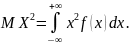
Если все значения случайной величины принадлежат интервалу то

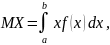
Пример 3.17. Непрерывная сл.в. задана плотностью распределения вероятностей

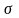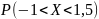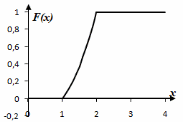
Найти: неизвестный параметр A, функцию распределения F(x), математическое ожидание , дисперсию среднее квадратичное отклонение и вероятность . Построить графики плотности и функции распределения.

Решение. По свойству 3 плотности

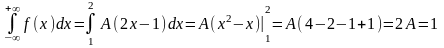, A=0,5.

Следовательно, функция с коэффициентом A=0,5 служит плотностью распределения вероятностей исследуемой случайной величины X, заданной в интервале (1;2).

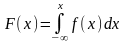,тогда:

при 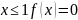и, следовательно,

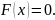
при

;

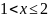
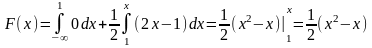при

.

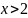
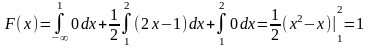Таким образом, функция распределения имеет вид:

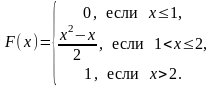
Графики плотности и функции распределения изображены на рис.3.3.

Рисунок 3.3

,

.

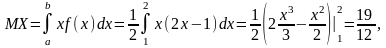
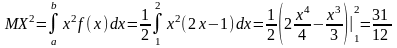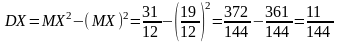Вероятность попадания величины в интервал

.

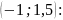
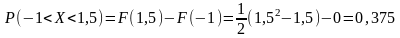11. Известна функция распределения сл.в. X:

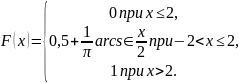
Найти: а) вероятность того, что в результате испытания сл.в. X примет значение из интервала ; б) (а) P=1/3; б) .)

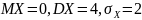12. Известна плотность распределения сл.в. X:

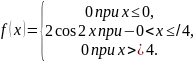
Найти: а) функцию распределения F(x) и вероятность того, что в результате испытания сл.в. X примет значение из интервала 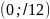; б) (а) P=0,5; б) .)

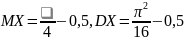13. Известна плотность распределения сл.в. X:

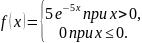
Найти: ( )
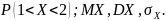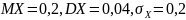