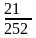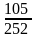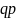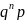2. Гипергеометрическое распределение

урновая модель. Изучается совокупность объёма N: M элементов первого типа и 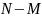элементов второго типа. Одновременном случайно отбирают из всей совокупности n элементов. Вероятность появления того или иного события описывается следующей схемой: пусть в урне 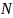шаров, из них 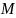белых и чёрных. Наудачу из урны вынимают n шаров. Найти вероятность, что среди них будет m белых шаров.

Поскольку порядок элементов здесь не важен, число всех возможных выборок объёма n из N элементов равен числу сочетаний из N по n 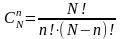. Число опытов, которые благоприятны появлению m белых шаров и остальных 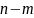чёрных шаров, равно 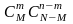. Рассмотрим сл. в. X – число белых шаров среди n отобранных шаров. Тогда вероятность того, что случайная величина X примет значение m, находится по формуле

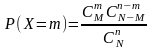. (3.8)

Про такую случайную величину говорят, что она имеет гипергеометрическое распределение с параметрами .

Пример 3.8. В аквариуме 10 рыбок, из них 3 рыбки золотые. Случайным образом отлавливают 5 рыбок. Составить закон и функцию распределения случайной величины – числа золотых рыбок среди пяти отловленных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.

Решение. Сл.в. – число золотых рыбок среди пяти отловленных. Сл.в. принимает значения 0, 1, 2, 3. Найдем вероятности этих значений:

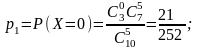
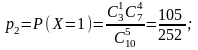
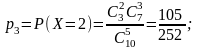
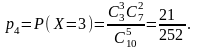
Запишем закон распределения в виде таблицы:

X	0	1	2	3
p

Найдём функцию распределения:

Для удобства построения графика функции распределения запишем рациональные дроби приближёнными десятичными:

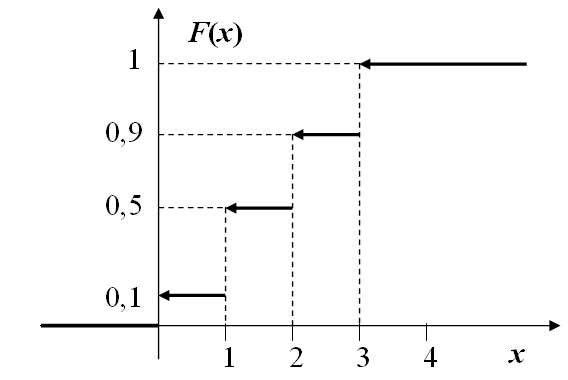
Рисунок 3.2

Вычислим математическое ожидание, дисперсию и среднее квадратичное отклонение по формулам (2.3), (2.5), (2.7).

Математическое ожидание:

.

Дисперсия:

Среднее квадратичное отклонение

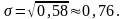
Пример 3.9. Производится стрельба по мишени до первого попадания без ограничения числа выстрелов. Найти закон распределения случайной величины – числа произведённых выстрелов, если вероятность попадания при каждом выстреле одна и та же и равна

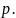
Решение. Сначала найдём вероятность того, что стрельба окончится 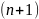-ым выстрелом (при первых выстрелах были промахи, а -ый выстрел – попадание). Так как вероятность произведения независимых событий равна произведению их вероятностей, то искомая вероятность

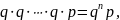
где 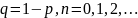. Тогда сл. в. – число произведённых выстрелов – имеет закон распределения, заданный таблицей:

	1	2

Это так называемый геометрический закон распределения. Можно показать, что математическое ожидание и дисперсия сл.в. находятся по формулам

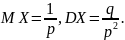
5. В ящике 2 белых и 3 черных шара. Наудачу извлекают 2 шара а) без возвращения; б) с возвращением. Сл.в. X – число извлечённых белых шаров. Составить закон распределения и функцию распределения сл.в. X, найти 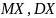. (а) .)

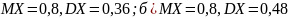6. Производится стрельба из орудия по удаленной цели. Вероятность попадания при первом выстреле равна 0,2. При каждом следующем выстреле вероятность увеличивается в 2 раза. Сл.в. X – число попаданий при трех выстрелах. Составить закон распределения, найти . (MX=1,4; DX=0,56.)

7. Студент пришел на зачет, зная 24 вопроса из 30. Преподаватель задает не более 3-х вопросов, но прекращает опрос и выставляет неудовлетворительную оценку, если студент не ответит на 2 вопроса подряд. Сл.в. X – число правильных ответов. Составить закон распределения, найти ( .)
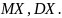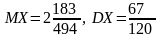