МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ им. И. И. ПОЛЗУНОВА

А.И.Гладышев, И.Ю.Гладышева, И.П.Мурзина, Т.М. Степанюк

Теория вероятностей

Учебно-методическое пособие

Барнаул 2013

УДК 519.21(075.5)

Гладышев А.И., Гладышева И.Ю., Мурзина И.П., Cтепанюк Т.М. Теория вероятностей. Учебно-методическое пособие для студентов технических специальностей / Алт. гос. техн. ун-т им. И.И.Ползунова. – Барнаул: 2013. – 32с.

Предлагаемая работа предназначена для организации самостоятельной работы студентов. Задания удобны для рейтинговой оценки знаний студентов. Подобраны равносильные варианты задач, при этом в большинстве задач отсутствует стереотипность формулировок и решений. В методических указаниях помещены сведения об основных формулах данной темы и примеры решения задач. Для более глубокого изучения материала приведён список литературы. Примерные варианты контрольных работ (с ответами) дают возможность произвести самоконтроль.

Рассмотрены и одобрены на заседании кафедры высшей математики и математического моделирования.

Протокол №5 от 29 апреля 2005г.

Рецензент: Е.М.Жданова

(к.ф.-м.н, доцент кафедры информационных технологий ААЭП)

Оглавление

1 Случайные события 4

1.1 Случайные события. Операции над событиями 4

1.2 Относительная частота и вероятность события 7

1.3 Методы комбинаторики 8

1.4 Геометрическая вероятность 11

1.4 Теоремы сложения и умножения вероятностей 13

1.5 Формула полной вероятности. Формула Байеса 17

2 Повторные независимые испытания 20

2.1 Формула Бернулли 21

2.2 Формулы Лапласа. Формула Пуассона 22

3 Случайные величины 29

3.1 Дискретные случайные величины 29

3.1 Числовые характеристики случайной величины 31

3.2 Гипергеометрическое распределение 36

3.4 Биномиальное распределение вероятностей 39

3.5 Непрерывные случайные величины 41

3.6 Равномерный закон распределе ния 44

3.7 Нормальный закон распределения 47

3.9 Показательный закон распределения 51

Вопросы для повторения 54

Обозначения

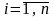– номер (индекс) i принимает все значения от единицы до n.

вероятность события A.

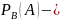вероятность события A при условии, что В произошло.

I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях независимо от их конкретной природы и дающая методы количественной оценки влияния случайных факторов на различные явления.

1. Случайные события

1. Случайные события. Операции над событиями

В теории вероятностей случайным событием A называют всё то, что может произойти или не произойти при осуществлении некоторого комплекса условий S. Событие наступает в результате различных процессов, которые называются опытами (экспериментами).

Если при реализации данного комплекса условий S событие A всегда произойдёт (никогда не произойдёт), то оно называется достоверным (невозможным).

Случайные события будем обозначать буквами A, B, C,…, достоверное событие – , невозможное –  . Примеры событий:

А – появление герба при бросании монеты;

В – выпадение чётного числа очков при игре в кости;

С – замерзание воды при сильном морозе;

D –выход из строя компьютера после пяти часов работы;

E – в перечне месяцев года после января идёт апрель.

События A, B, D случайные, событие C достоверное, а событие E невозможное.

События, не разложимые на более простые, называются элементарными событиями (исходами). Множество всех элементарных исходов данного опыта образуют пространство элементарных событий . Любое событие A можно рассматривать как подмножество . Так, при бросании игральной кости пространство элементарных событий состоит из шести элементарных исходов:

.

Событие B={выпадение четного числа очков при игре в кости} состоит из трех элементарных исходов – 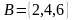, событие {выпадение числа очков, кратного 3} – из двух элементарных исходов.

Суммой событий называется событие, состоящее в наступлении или , или , или обоих событий вместе. Сумму событий обозначают или

Событие или обозначает наступление хотя бы одного из событий .

Пример 1.1. В урне шесть шаров, отличающихся только номером . Наугад выбирают один шар. Обозначим событие . Событие состоит в том, что будет выбран шар с номером 1 или 3, или 5, т.е. шар с нечётным номером.

Произведением событий называют событие B, состоящее в наступлении всех этих событий. Обозначение произведения событий:

Пример 1.2. Есть колода игральных карт. Наугад берут одну карту. Обозначим события A = {вынут туз}, B = {вынута карта красной масти}. Тогда событие C = A∙B означает «вынут туз красной масти».

Разностью событий A и B (обозначается ), называется событие D, состоящее в наступлении события A и одновременном не наступлении события В. Для предыдущего примера событие означает, что выбран туз чёрной масти.

Если при каждой реализации комплекса условий S, когда происходит событие A, происходит и событие B, то будем говорить, что A влечёт за собой B, и обозначать этот факт или .

Если имеет место одновременно и , то события называются равносильными. В этом случае пишут .

События называются несовместными, если в результате одного опыта никакие два из них не могут произойти одновременно:

.

Два несовместных события, из которых одно должно обязательно произойти, называются противоположными. Обозначаются они . При этом . очевидно, что .

Совокупность событий называется полной группой несовместных событий, если

.

Примером полной группы несовместных событий является пространство элементарных событий. Другой характерный пример – пара двух противоположных событий: . Например, выпадение герба и решки при однократном подбрасывании монеты, работоспособность компьютера и его неисправность в данный момент времени, попадание и непопадание в мишень при одном выстреле и т.д.

1. В урне 4 красных и 6 белых шаров. Все они пронумерованы от 1 до 10. Урны берут наудачу 1 шар. Событие – шар с чётным номером – обозначим через A, с номером, кратным 3, – через B, шар красного цвета – через C и шар белого цвета – через D. что представляют собой следующие события:

2. Докажите равенства:

3. При каких условиях справедливы следующие соотношения:

4. Установите, какие из следующих соотношений верны:

5. Упростите выражения:

6. На контрольной работе было 3 задачи. Событие – студент решил 1-ую задачу – обозначим через A, решил 2-ую задачу – через B и решил 3-ю задачу – через C. Найти выражения для следующих событий:

а) студент решил только 1-ую задачу;

б) решил только одну задачу;

в) решил только две задачи;

г) решил все задачи;

д) решил, по крайней мере, одну задачу;

е) решил не более двух задач.