2.1.Рівняння Пуассона
Це
рівняння має вигляд: 
де 
- оператор
Лапласа або лапласіан,
а 
- речова або комплексна функція на
деякому різноманітті.
У тривимірній декартовій системі координат рівняння приймає форму:
В декартовій
системі координат оператор
Лапласа записується у формі 
і
рівняння Пуассона приймає вигляд:
Якщо f прямує до нуля, то рівняння Пуассона перетворюється в рівняння Лапласа (рівняння Лапласа - окремий випадок рівняння Пуассона):
Рівняння Пуассона може бути вирішено з використанням функції Гріна; див., наприклад, статтю екранувати рівняння Пуассона. Є різні методи для отримання чисельних рішень. Наприклад, використовується ітераційний алгоритм - "релаксаційний метод".
2.2. Електростатика
Рівняння Пуассона є одним з наріжних каменів електростатики. Знаходження φ для даного f - важлива практична задача, оскільки це звичайний шлях для знаходження електростатичного потенціалу для даного розподілу заряду. В одиницях системи СІ :
де 
-
Електростатичний потенціал (в вольтах), 
-
Об'ємна щільність
заряду (в кулонах на
кубічний метр), а 
- діелектрична
проникність вакууму(в Фарада на
метр).
В одиницях системи СГС :
В області простору, де немає непарної щільності заряду, маємо:
і рівняння для потенціалу перетворюється в рівняння Лапласа :
2.3. Потенціал точкового заряду
Потенціал, джерелом якого служить точковий заряд,
- Тобто кулонівський потенціал - є по суті (а строго кажучи при q = 1) функція Гріна
для рівняння Пуассона,
тобто рішення рівняння
де 
-
Позначення дельта-функції
Дірака,
а твір трьох дельта-функцій є тривимірна
дельта-функція, а 
У зв'язку з цим зрозуміло, що рішення рівняння Пуассона з довільною правою частиною може бути записано як
Тут ми маємо на увазі найбільш простий випадок "без граничних умов", коли приймається, що на нескінченності рішення повинне прагнути до нуля. Розгляд більш загального випадку довільних граничних умов і взагалі більш детальний виклад - див. в статті Функція Гріна.
Фізичний зміст останньої формули - застосування принципу суперпозиції (що можливо, оскільки рівняння Пуассона лінійно) і знаходження потенціалу як суми потенціалів точкових зарядів
.
2.4. Потенціал гауссових об'ємної щільності заряду
Якщо
ми маємо об'ємну сферично симетричну
густину гауссового
розподілу заряду 
:
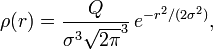
де Q - загальний заряд, тоді рішення Φ (r) рівняння Пуассона:
дається:
де
erf (x) - функція
помилок.
Це рішення може бути перевірено
безпосередньо обчисленням 
.
Зауважте, що для r, багато
більших, ніж σ, erf (x)наближається
до одиниці, і потенціал Φ (r) наближається
до потенціалу
точкового заряду 
,
Як і можна було очікувати.
Література
Федорченко А. М. Квантова механіка, термодинаміка і статистична фізика // Теоретична фізика. — К.: Вища школа, 1993. — Т. 2. — 415 с.
Базаров И. П. Термодинамика. — М.: Высшая школа, 1991. — 376 с.
Залевски К. Феноменологическая и статистическая термодинамика. — М.: Мир, 1973. — 168 с.
Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1 // Теоретическая физика. — М.: Физматлит, 2005. — Т. 5. — 616 с.
Леонтович М. А. Введение в термодинамику. — М.: ГИТТЛ, 1950. — 184 с.
Лоренц Г. А. Лекции по термодинамике. — М.-Л.: ГИТТЛ, 1946. — 156 с.
Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. — М.: Мир, 2002. — 464 с.
Ферми Э. Термодинамика. — Х.: Изд-во ХГУ, 1969. — 140 с.
Эпштейн П. С. Курс термодинамики. — М.: ГИТТЛ, 1948. — 420 с.
Міністерство освіти та науки
Реферат з фізики на тему: «Рівноважні процеси.Рівняння Пуассона» Виконав: студент 2д-926 групи ЖАДК Антонюк Д.О. Викладач: Кулікова Л.М.
2013
План
1.Термодинаміка 1.2. Історія термодинаміки 1.3. Основні поняття термодинаміки 1.4. Адіабатичний процес. Рівняння Пуассона. Політропічні процеси. Робота газу при політропічних процесах. Другий та третій закони термодинаміки. Ентропія. Цикл Карно.
2.1.Рівняння Пуассона 2.2.Електростатика 2.3.Потенціал точкового заряду 2.4.Потенціал гаусових об’ємних щільності заряду 3.Література