§13. Касательная и нормаль к линии.
Из геометрического смысла производной
следует, что если нам известно уравнение
некоторой линии
в системе декартовых координат
на плоскости,то мы можем аналитически
решать геометрические задачи, относящиеся
к касательной к этой линии.Прежде всего
составим уравнение касательной к линии
в ее точке
где
Так
касательная прямая проходит через точку
и имеет угловой коэффициент, равный
то
ее уравнение таково:
Определение.
Нормалью к линии в ее точке
называется прямая ,проходящая через
точку
и перпендикулярная к касательной в
той же точке.
Так как нормаль к линии в точке проходит через точку и имеет угловой коэффициент, равный
то
ее уравнение таково:
Пример.
Написать уравнение касательной и нормали
к кривой
в точке
Решение. Так как
то угловой коэффициент касательной
равен
Следовательно, уравнение касательной:
или
Уравнение нормали:
или
Вариант 1.
Найти производные следующих функций:
Вариант 2.
Найти производные следующих функций:
Вариант 3
Найти производные следующих функций:
Вариант 4
Найти производные следующих функций:
Вариант 5
Найти производные следующих функций:
Вариант 6
Найти производные следующих функций:
Вариант 7
Найти производные следующих функций:
Вариант 8
Найти производные следующих функций:
Вариант 9
Найти производные следующих функций:
Вариант 10
Найти производные следующих функций:
Вариант 11
Найти производные следующих функций:
Вариант 12
Найти производные следующих функций:
Вариант 13
Найти производные следующих функций:
Вариант 14
Найти производные следующих функций:
Вариант 15
Найти производные следующих функций:
Вариант 16
Найти производные следующих функций:
Вариант 17
Найти производные следующих функций:
Вариант 18
Найти производные следующих функций:
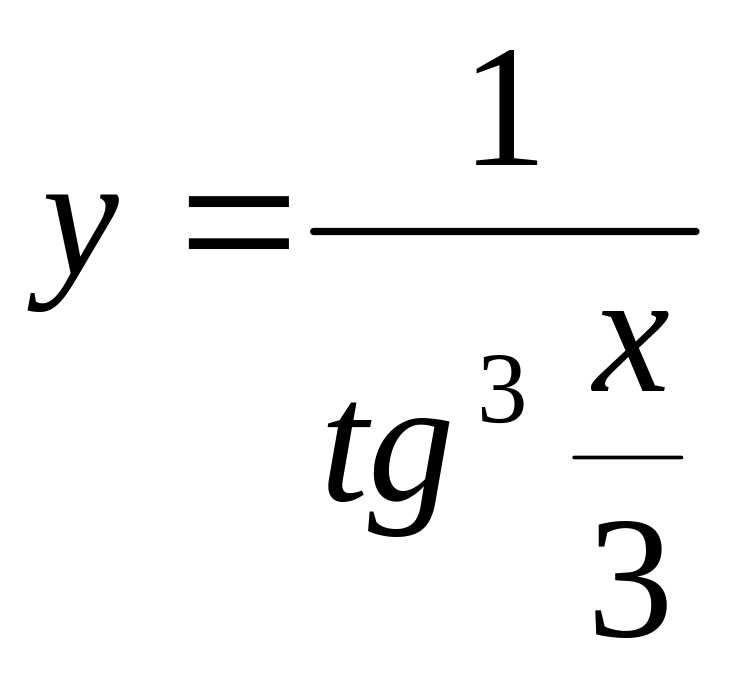
Вариант 19
Найти производные следующих функций:
Вариант 20
Найти производные следующих функций:
Вариант 21
Найти производные следующих функций:
Вариант 22
Найти производные следующих функций:
Вариант 23
Найти производные следующих функций:
Вариант 24
Найти производные следующих функций:
Вариант 25
Найти производные следующих функций:
