§8. Производные обратных тригонометрических функций.

Пусть y=arcsinx, где -1≤x≤1 и

Обратная функция имеет вид x=siny, причем если

Используя правило дифференцирования обратной

функции,получим

Так как при то, получаем

Следовательно, имеем т.е. (

2. Пусть y=arccosx, тогда x=cosy, причем -1≤x≤1 и 0≤y≤π.

На основании правила дифференцирования обратной функции имеем

Так как siny>0 при 0<y<π, то

Поэтому

Таким образом,

3.Пусть y=arctgx и , следовательно , x=tgy.

Имеем

Таким образом,

4.Пусть y=arcctgx

тогда x=ctgy.

Имеем

т.е.

Пример.

§9. Производная показательной функции.

Для нахождения производной показательной функции воспользуемся правилом дифференцирования обратной функции.

Если то и

Отсюда

Следовательно,

Таким образом,

В частности, если то

Примеры.

1.

2.

4.

§10.Таблица основных формул дифференцирования.

На этом этапе темы «Производная» целесообразно составить следующую таблицу производных , где F – одна из основных элементарных функций. Напомним, что основными элементарными функциями принято называть следующие: степенную функцию , показательную функцию , логарифмическую функцию , четыре тригонометрические функции и четыре обратные тригонометрические функции .

1
2
3
4
5
6
7
8
9
10
11
12
13

Пример .

Найдите производную функции .

Решение. Согласно формулам 5) и 7) имеем:

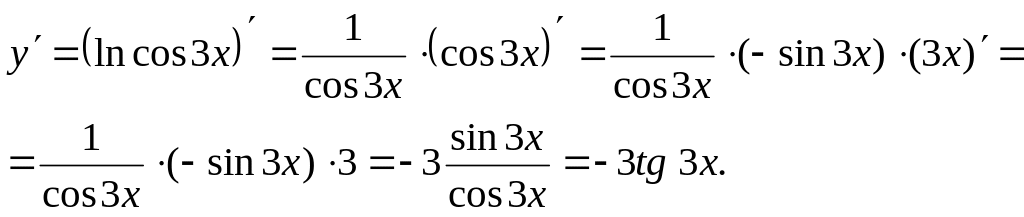
Найдите производные следующих функций:

1) ; 9)

2) 10)

3) 11)

4) 12)

5) 13)

6) 14)

7) 15)

8) 16)