Контекстный анализ

Основная идея контекстного анализа заключается в том, что анализу подвергается не весь текст, а лишь некоторая выборка из него, являющаяся контекстом употребления характеристики c. Есть много способов задать контекст. Например, для слова (характеристики) w в качестве его контекста мы можем взять все предложения (абзацы, статьи, книги), в которых оно встречается. Вместо предложений мы можем считать контекстом по одному или более слов слева и справа от каждого вхождения w в текст.

Если текст t рассматривать как множество предложений, а предложение s рассматривать как множество слов, то контекст категории C в тексте t можно определить как

ctx(C,t)={s-{w}: w входит в C, w входит в s, s входит в t}.

Выделенный контекст может анализироваться как самостоятельно, так и относительно основного текста. Во втором случае основной текст служит источником норм, которые затем используются при анализе контекста. Т.е. во втором случае для произвольной категории K мы интересуемся условной частотой pr(K,ctx(C,t)) и сравниваем ее с нормой nr(K,t), вычисляемой как pr(K,t-{C}), где t-{C}={s-{w}: w входит в C, s входит в t}

Дополнительно к этому мы можем выделить множество слов

col(C,t)={w: pr(w,ctx(C,t)) существенно больше pr(w,t-{C})}

В англоязычной литературе по контент-анализу такое множество называется collocation категории C. Отношение существенно больше валидизируется с помощью аппарата математической статистики по аналогии с тем, как это описывалось выше. Множество col(C,t) содержит много полезной информации о категории C. Например, col({змея},речь) будет содержать такие слова как яд, кусать, ползать, пресмыкающееся,…, а в col({Путин},СМИ) войдут слова Владимир, президент, Кремль, Россия,….

Связи категорий

Мы можем интересоваться не только оценками данного текста по отдельных категориям, но и их взаимосвязями.

Любому тексту t, рассматриваемому как последовательность предложений , и категории C может быть сопоставлен булев вектор b(t,C)=, где vi=1, если для некоторого w из C w входит в si, и vi=0 в противном случае. На множестве векторов легко определить логические операции. Для двух векторов b(t,Ci)= и b(t,Cj)= они определяются следующим образом

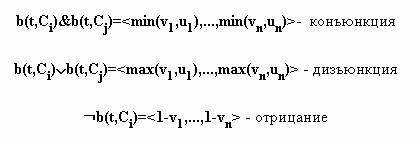
Затем на множестве векторов можно ввести логические отношения совместности, противоречия, подчинения и пр. Очевидно, что таким образом задается некоторая логическая модель предметной области, о которой идет речь в тексте, или же модель когнитивной карты, присущей автору текста. Дальнейшее изучение этих моделей проводится с использованием аппарата классической, многозначной или вероятностной логики высказываний.

Особый интерес представляет анализ и визуализация отношений между категориями с использованием аппарата многомерного шкалирования, кластерного и факторного анализа.

Определим на множестве категорий (булевых векторов, сопоставленных категориям) функцию близости. Для каждого вектора b(t,Ci)= вычисляется оценка

Тогда коэффициент корреляции для булевых векторов вычисляется следующим образом

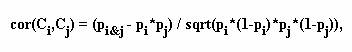
а функцию близости можно определить как

Также в качестве оценки близости двух категорий часто используется метрика Хемминга, определяемая посредством формулы