3 Проектный расчет червячной передачи с цилиндрическим червяком

3.1 Исходные данные

3.1.1 Схема передачи (рис. 1.1), задана техническим заданием.

3.1.2 Циклограмма нагружения (рис. 1.2) передачи, задана техническим заданием.

3.1.3 Срок службы передачи L=5 лет, согласно техническому заданию; режим работы (продолжительность включения) ПВ=1,0; работа двухсменная; К_год = 0,67.

3.1.4 Номинальный вращающий момент на валу колеса проектируемой червячной передачи, Н мм:

3.1.5 Передаточное число проектируемой червячной передачи U = 18,8.

3.1.6 Номинальная частота вращения вала червяка n₁ = 1425 мин^-1.

3.2 Выбор материалов червячной пары

3.2.1 Червяк изготавливаем из стали 18ХГТ, упрочняющая химико-термическая обработка – цементация с закалкой до твердости HRC_э 56…63.

3.2.2 Для выбора материала червячного колеса определяем: - скорость скольжения в зацеплении [1, с. 212]

, м/с; (3.1) - коэффициент эквивалентности при расчете по контактным напряжениям [1, с. 76, ф. 4.1]

; (3.2) - произведение

. (3.3)

3.2.3 Выбираем группу материалов [1, с. 213, табл. 7.2].

Т.к. , то выбираем материал гр. Iа.

Назначаем для изготовления червячного колеса бронзу Бр 010Ф1, способ получения заготовки – литье в кокиль.

Механические характеристики принятой бронзы:

МПа; МПа.

3.3 Для материала червячного колеса определяем допускаемые напряжения [1, с. 214, табл. 7.3]

3.3.1 Допускаемое контактное напряжение , где C_V = 1,07 – коэффициент, учитывающий износ.

МПа. (3.4)

3.3.2 Допускаемое напряжение изгиба

МПа. (3.5)

3.3.3 Максимальные допускаемые напряжения при расчете по пиковой нагрузке

МПа, (3.6)

МПа. (3.7)

3.4 Проектный расчет червячной передачи

Учитывая, что для бронз I группы расчет выполняют по эквивалентному моменту, определяем коэффициент долговечности К_НД и К_FД.

3.4.1 Коэффициент долговечности при расчете по контактным напряжениям

, (3.8) где К_НЕ = 0,866; N_HG = 10⁷ – условная база при определении удела контактно-износной выносливости материала; - число циклов нагружения зубьев колеса за весь срок службы.

; (3.9)

.

3.4.2 Коэффициент долговечности при расчете по напряжениям изгиба.

, (3.10) где N_FG =10⁶ – условная база при определении предела изгибной выносливости материала; K_FE – коэффициент эквивалентности при расчете по напряжениям изгиба.

; (3.11)

.

3.4.3 Предварительное значение межосевого расстояния червячной передачи из условия контактной прочности зубьев колеса:

, (3.12) где - расчетный момент; (3.13) - предварительное значение коэффициента нагрузки [1, с. 216].

Коэффициент концентрации нагрузки . (3.14)

По данным [1, с. 214, рис. 7.2] при u = 18,8 и числе витков червяка z₁ = 2 имеем .

.

Коэффициент динамичности нагрузки К’_v = 1, [1, с. 215].

;

Н мм;

мм.

Принимаем стандартное межосевое расстояние мм.

3.4.4 Число зубьев колеса

. (3.15)

3.4.5 Модуль зацепления [1, с. 216]

. (3.16)

Принимаем стандартный модуль m = 5 мм.

3.4.6 Коэффициент диаметра червяка [1, с. 216]

. (3.17)

Стандартное значение q’ =11,2.

3.4.7 Коэффициент смещения [1, с.216]

. (3.18)

Окончательно принимаем:

m = 5 мм; а = 112 мм; q = 11,2; z₂ = 40; = 0.

3.4.8 Проверяем фактические контактные напряжения:

, МПа, (3.19) где мм – делительный диаметр червяка; мм – начальный диаметр червяка.

Расчетный момент .

Для нахождения уточненного значения коэффициента нагрузки находим: - угол подъема винта червяка на начальном диаметре

; (3.20) - фактическая скорость скольжения в зацеплении

м/с. (3.21)

Окружная скорость колеса

м/с. (3.22)

Уточненное значение коэффициента концентрации

, (3.23) где - коэффициент деформации червяка; - коэффициент режима [1, с. 215]. (3.24)

.

Коэффициент динамической нагрузки [1, с. 215, с. 96] (при 8 степ. Точности и м/с).

;

Н мм.

МПа.

3.4.9 Уточняем допускаемое контактное напряжение с учетом фактической скорости V_CK :

МПа, при С_V = 0,9.

Условие контактной прочности .

Процент перегрузки

. (3.25)

Перегрузка составила 3%.

3.4.11 Проверяем прочность зубьев колеса по напряжениям изгиба

, (3.27) где Y_F – коэффициент деформации зуба, определяемый в зависимости от эквивалентного числа зубьев колеса

; (3.28)

Y_F = 1,63.

Коэффициент долговечности по изгибу

K_FД = 1,56.

Окружное усилие на колесе

Н. (3.29)

МПа < МПа.

3.4.12 Проверяем статическую прочность зубьев колеса на изгиб при действии пиковой нагрузки

МПа < МПа.

3.4.13 Основные геометрические размеры червяка.

Делительный диаметр мм.

Диаметр вершин витков мм.

Диаметр впадин витков мм.

Длина нарезанной части червяка мм.

b₁ = 100 мм – соответствует главным параметрам.

3.4.14 Основные геометрические размеры червячного колеса (рис. 3.1).

Делительный диаметр мм.

Диаметр вершин зубьев мм.

Диаметр впадин зубьев мм.

Наибольший диаметр колеса мм.

Радиус закругления колеса мм.

Ширина венца мм.

Принимаем b₂ = 40 мм.

3.4.15 Усилия, действующие в червячном зацеплении:

Н;

, (3.30) где КПД червячной передачи , где - приведенный угол трения.

При V_CK = 4,244 [1, с. 226].

.

Н.

Н

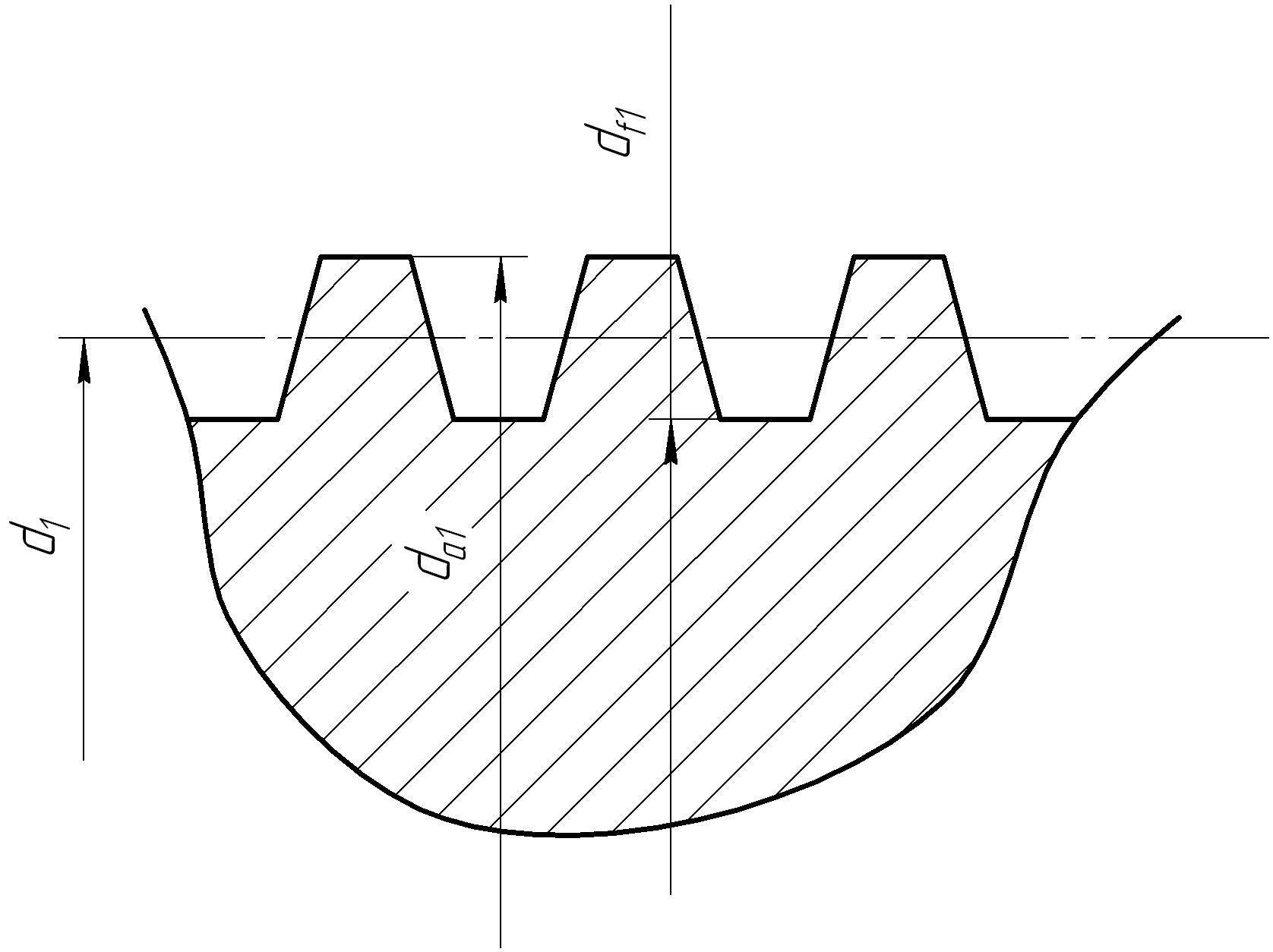
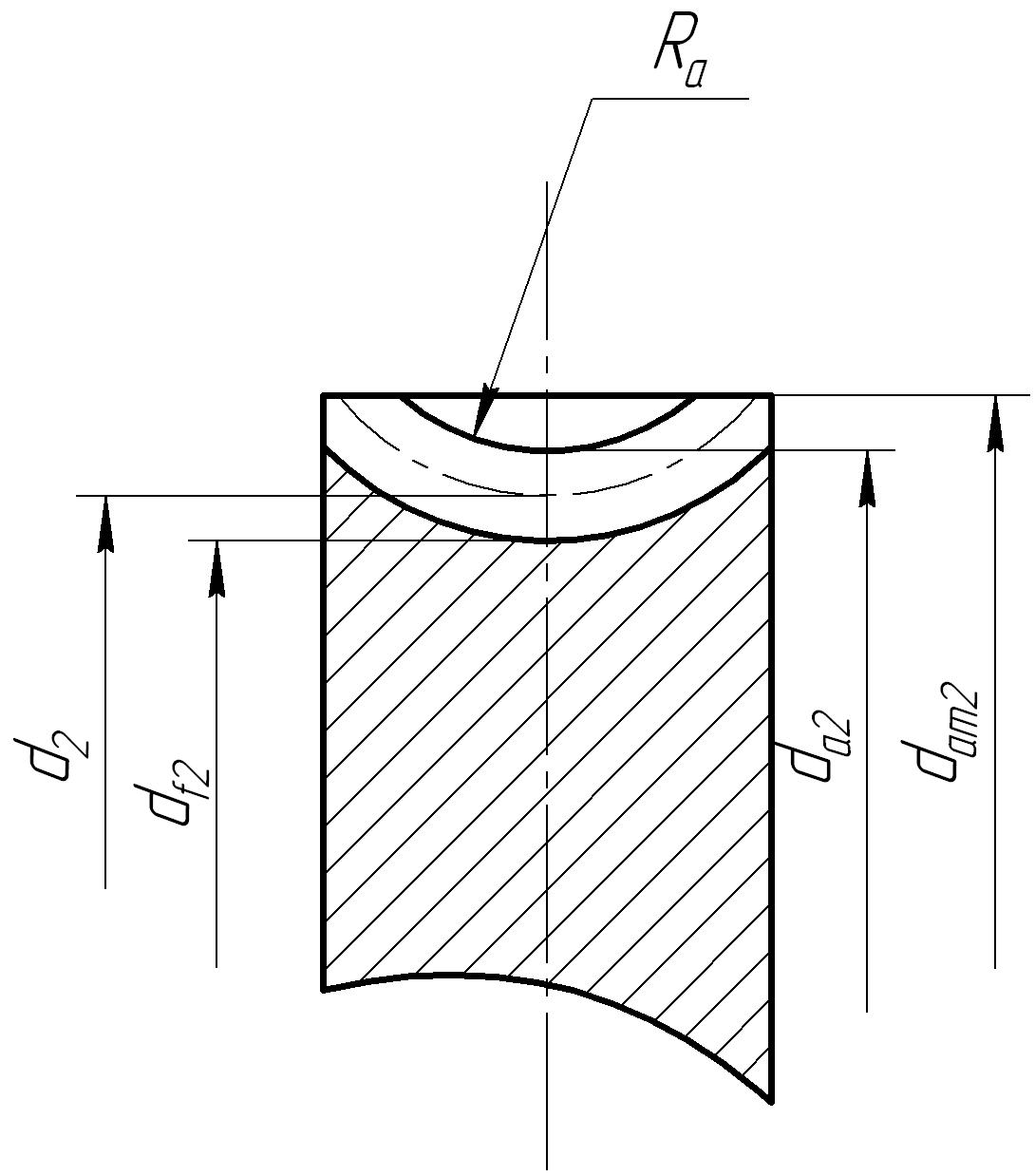
Рисунок 3.1 – Основные размеры червяка и червячного колеса.