Анализ статистической значимости коэффициента детерминации
После оценки индивидуальной статистической значимости каждого из коэффициентов регрессии обычно анализируется совокупная значимость коэффициентов, то есть гипотеза об общей значимости — гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при объясняющих переменных:
|
|
.Проверка данной гипотезы осуществляется на основе дисперсионного анализа сравнения объясненной и остаточной дисперсий.
|
|
(объясненная
дисперсия)=(остаточная дисперсия),
(объясненная
дисперсия)>(остаточная
дисперсия).Строится F-статистика:
|
(6.35) |
,
где
- объясненная дисперсия,
- остаточная дисперсия. При выполнении
предпосылок МНК построенная
F-статистика
имеет распределение Фишера с числами
степеней свободы
,
.
Если при
требуемом уровне значимости
(где
- критическая точка распределения
Фишера), то
отклоняется в пользу
,
то есть объясненная
дисперсия существенно больше остаточной
дисперсии, а значит уравнение регрессии
качественно отражает динамику изменения
зависимой переменной Y.
Если
,
то нет оснований для отклонения
,
то есть объясненная
дисперсия соизмерима с дисперсией,
вызванной случайными факторами, и
совокупное влияние объясняющих
переменных модели
несущественно, а следовательно, общее
качество модели
невысоко.
На практике вместо указанной гипотезы проверяют гипотезу о статистической значимости коэффициента детерминации :
,
.
Для проверки данной гипотезы используется следующая F-статистика:
|
(6.36) |
.
Очевидно,
что показатели F
и
равны
или не равны нулю одновременно. Нулевая
гипотеза отклоняется, если
.
Это
равносильно тому, что
,
т.е.
статистически
значим.
Однако статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации не гарантирует высокое качество уравнения регрессии.
Статистика Дарбина—Уотсона
Наиболее известным критерием обнаружения автокорреляции между соседними членами является критерий Дарбина-Уотсона. Он основан на простой идее: если корреляция ошибок регрессии не равна нулю, то она присутствует и в остатках регрессии получающихся в результате применения обычного метода наименьших квадратов.
Для анализа коррелированности отклонений вместо коэффициента корреляции
|
(6.37) |
|
|
,используют тесно с ним связанную статистику Дарбина-Уотсона DW, рассчитываемую по формуле
|
(6.38) |
.
Действительно,
.
Здесь
сделано допущение, что для больших
справедливо соотношение:
.
Тогда
|
(6.39) |
.
Если
,
то
(положительная автокорреляция) и
.
Если
,
то
(отрицательная автокорреляция) и
.
Если
(автокорреляция отсутствует), то
.
Во всех других случаях
.
Необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина—Уотсона. Тогда, если , мы считаем отклонения от регрессии случайными.
Это означает, что:
построенная линейная регрессия, вероятно, отражает реальную зависимость;
скорее всего, не осталось неучтенных существенных факторов, влияющих на зависимую переменную;
какая-либо другая нелинейная формула не превосходит по статистическим характеристикам предложенную линейную.
Возникает
вопрос, какие значения DW
можно
считать статистически
близкими к двум? Для
ответа на этот вопрос разработаны
специальные таблицы
критических точек статистики
Дарбина—Уотсона,
позволяющие при данном числе наблюдений
,
количестве
объясняющих переменных
и
заданном уровне значимости
определять границы приемлемости
(критические точки) наблюдаемой статистики
DW.
Для
заданных
,
,
в таблице указываются
два числа:
- нижняя граница и
-
верхняя
граница. Для проверки
гипотезы об отсутствии автокорреляции
остатков используется
числовой отрезок, изображенный на рис.
6.3.
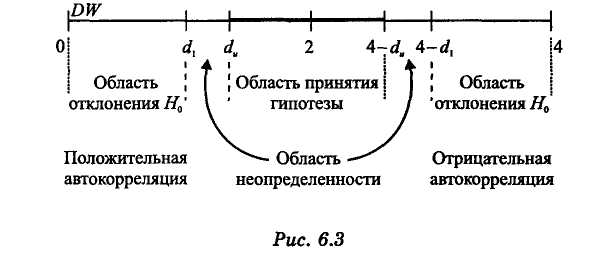
Выводы осуществляются по следующей схеме.
Если
,
то это свидетельствует о положительной
автокорреляции
остатков.
Если
,
то это свидетельствует об отрицательной
автокорреляции
остатков.
При
гипотеза
об отсутствии автокорреляции
остатков принимается.
Если
или
,
то гипотеза об
отсутствии автокорреляции не может
быть ни принята, ни отклонена.
Не
обращаясь к таблице критических точек
Дарбина—Уотсона,
можно пользоваться «грубым» правилом
и считать, что автокорреляция
остатков отсутствует, если
.
При наличии автокорреляции остатков полученное уравнение регрессии обычно считается неудовлетворительным.