§ 3.6. Умножение вектора на j и —j.

Рис.14

Пусть есть некоторый вектор   (рис. 3.8). Умножение его на j дает вектор, по модулю равный А, но повернутый в сторону опережения (против часовой стрелки, по отношению к исходному вектору на 90°. Умножение на   поворачивает вектор на 90° в сторону отставания (по часовой стрелке) также без изменения его модуля. Чтобы убедиться в этом, представим векторы j и -j в показательной форме:

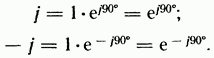
Тогда

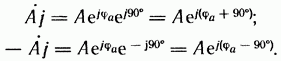
§ 3.7. Основы символического метода расчета цепей синусоидального тока.

Очень широкое распространение на практике получил символический, или комплексный, метод расчета цепей синусоидального тока.

Сущность символического метода расчета состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями, к алгебраическим уравнениям, составленным относительно комплексов тока и ЭДС. Этот переход основан на том, что в уравнении, составленном по законам Кирхгофа для установившегося процесса, мгновенное значение тока i заменяют комплексной амплитудой тока   мгновенное значение напряжения на резисторе сопротивлением R, равное   — комплексом   по фазе совпадающим с током   мгновенное значение напряжения на индуктивной катушке   — комплексом опережающим ток на 90°; мгновенное значение напряжения на конденсаторе  — комплексом   отстающим от тока на 90°; мгновенное значение ЭДС е — комплексом   Справедливость замены   на  .

В § 3.8 было показано, что амплитуда напряжения на L равна произведению амплитуды тока на   Множитель j свидетельствует о том, что вектор напряжения на индуктивной катушке опережает вектор тока на 90°.

Аналогично, из § 3.9 следует, что амплитуда напряжения на конденсаторе равна амплитуде тока, умноженной на   Отставание напряжения на конденсаторе от протекающего по ней тока на 90° объясняет наличие множителя –j.

Рис.15

Например, для схемы рис. 15 уравнение для мгновенных значений можно записать так: или

Запишем его в комплексной форме:

Вынесем   за скобку:

Следовательно, для схемы рис.15

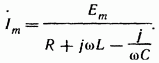
Метод называют символическим потому, что токи и напряжения заменяют их комплексными изображениями или символами.

§ 3.8. Комплексное сопротивление. Закон Ома для цепи синусоидального тока.

Множитель    представляет собой комплекс, имеет размерность сопротивления и обозначается через Z. Его называют комплексным сопротивлением:

Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через z. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени.

Разделим обе его части на и перейдем от комплексных амплитуд  к комплексам действующих значений 

В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть  (1) где R — активное сопротивление; X — реактивное сопротивление. Для схемы (рис. 1) реактивное сопротивление
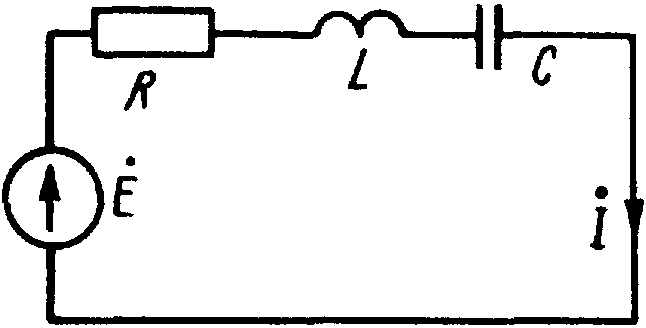