§ 3.3 Синусоидальный ток в активном сопротивлении.
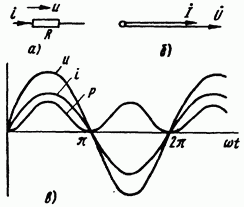Рис.9
На Рис.9а изобр. активное сопротивление R по которому течёт ток.
(1)
Векторная
диаграмма комплекса тока 
и
совпадающего с ним по фазе комплекса
напряжения
показана на рис.9б.
На
рис.9в даны кривые мгновенных значений
тока i, напряжения u и
мощности 
Мгновенная
мощность p имеет
постоянную составляющую 
и
составляющую 
изменяющуюся с частотой 
Потребляемая
от источника питания за время 
энергия
равна 
§ 3.4. Индуктивность цепи синусоидального тока.
Векторной диаграммой называют совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной ориентации их относительно друг друга по фазе.
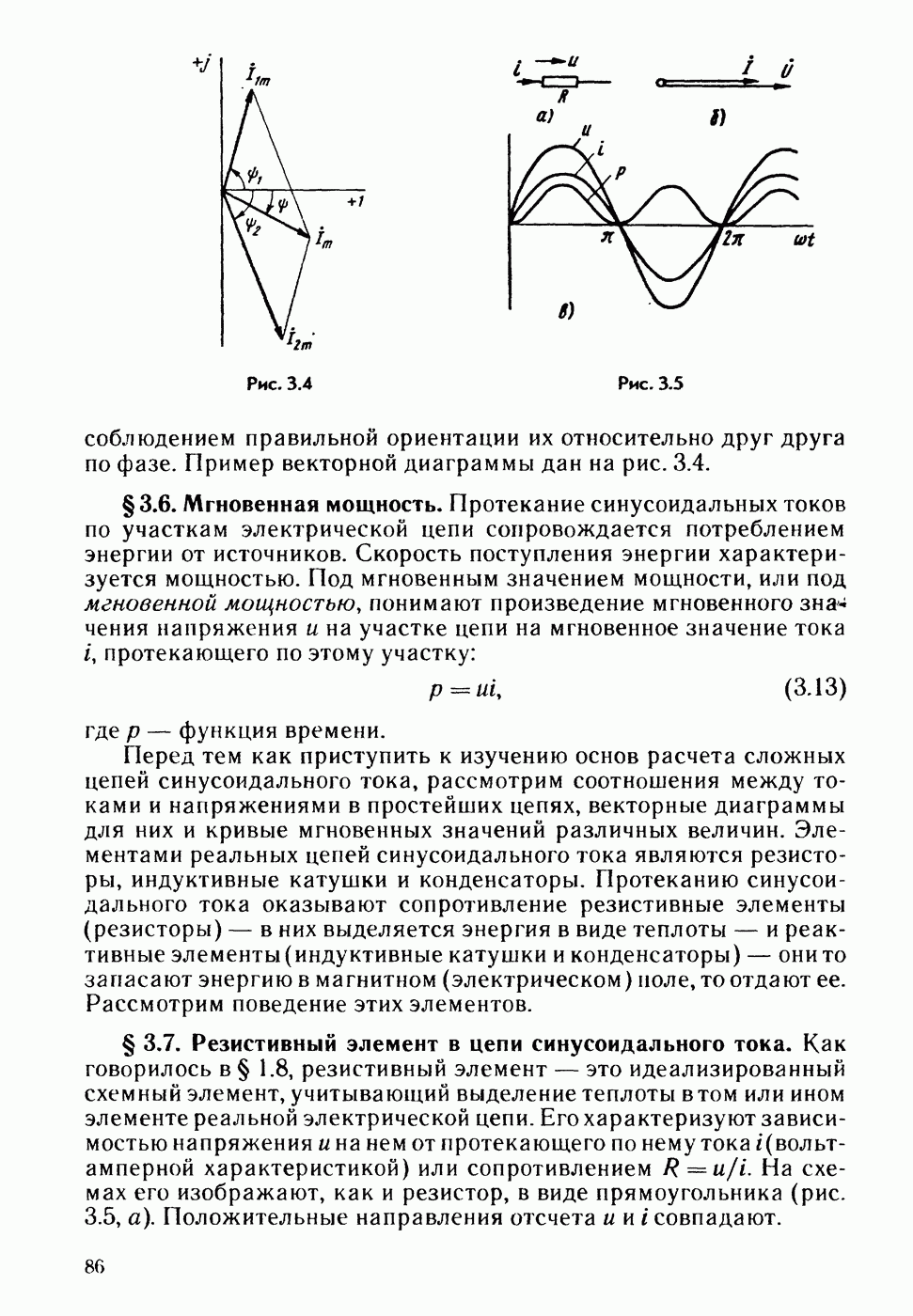Рис.10
На рис.11 катушку можно представить в виде последовательно соединенных индуктивного и резистивного элементов.
Рис.11
Выделим
индуктивный элемент (рис.11). Положительные
направления тока i через него, ЭДС
самоиндукции 
и
напряжение на нем 
указаны
на рис.11а. Если 
то 
.
Определим разность потенциалов между
точками a
и b. При
перемещении от точки b к точке а идем
встречно ЭДС
поэтому,
и
Дальнейшем
напряжение на индуктивном элементе
будем обозначать 
или,
просто, u
без индекса
Следовательно,
Таким
образом, индуктивный элемент (индуктивная
катушка, у которой 
) при
синусоидальном токе обладает
сопротивлением, модуль которого 
прямо
пропорционален частоте 
— на рис.11б вектор напряжений
опережает вектор тока
на
90°.
§ 3.5. Конденсатов в цепи синусоидального тока.
Если
приложенное к конденсатору напряжение
и не изменяется во времени, то заряд 
на
одной его обкладке и заряд —q на другой
(С — емкость конденсатора) неизменны,
и ток через конденсатор не проходит 
Рис.12
Если
же напряжение на конденсаторе изменяется
во времени, например по синусоидальному
закону (рис.12а):
(1)
то по синусоидальному закону будет
меняться и заряд q конденсатора: 
т.
е. конденсатор будет периодически
перезаряжаться.
Периодическая
перезарядка конденсатора сопровождается
протеканием через него зарядного
тока:
(1а)
Из
сопоставления (1) и (1а) видно, что ток
через конденсатор опережает по фазе
напряжение на конденсаторе на 90°. Поэтому
на векторной диаграмме (рис. 12б)
вектор 
опережает
вектор напряжения 
на
90°. Амплитуда тока 
равна
амплитуде напряжения 
деленной
на емкостное сопротивление:
Если
проинтегрировать по времени обе части
равенства
то
получим
(2).
Равенство (2) позволяет определить
напряжение на конденсаторе через ток
по конденсатору.
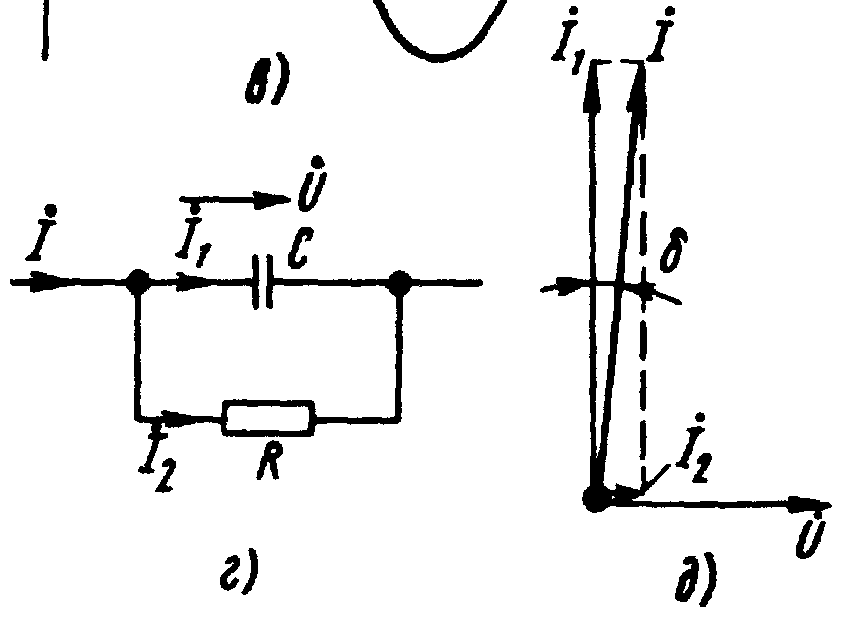
Рис.13 схема замещения реального конденсатора.
Ток 
опережает
U на 90°, а ток 
совпадает
с
по фазе. Угол
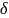называют углом потерь; 
где 
—
добротность конденсатора, 
зависит
от типа диэлектрика и от частоты и
изменяется от нескольких секунд до
нескольких градусов.