§ 3.1 Среднее и действующее значения синусоидально изменяющейся величины.

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока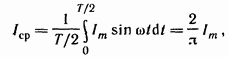

т. е. среднее значение синусоидального тока составляет   от амплитудного. Аналогично, 

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,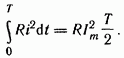

Выделенная за то же время постоянным током теплота равна   Приравняем их:

Таким образом, действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

§ 3.2. Комплексная плоскость. Комплексная амплитуда. Комплекс действующего значения.

На рис.7 дана комплексная плоскость, на которой можно изобразить комплексные числа. Комплексное число имеет действительную (вещественную) и мнимую части. По оси абсцисс комплексной плоскости откладывают действительную часть комплексного числа, а по оси ординат — мнимую часть.

Рис.7

На оси действительных значений ставим +1, а на оси мнимых значений 

(1) - формула Эйлера

Комплексное число   изображают на комплексной плоскости вектором, численно равным единице и составляющим угол а с осью вещественных значений (осью +1). Угол отсчитываем против часовой стрелки от оси +1. Модуль функции

Проекция функции   на ось +1 равна 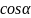 , а на ось +j равна  . Если вместо функции   взять функцию   то

На комплексной плоскости эта функция, так же как и функция   изображается под углом к оси +1, но длина вектора будет в   раз больше.

Угол а в формуле (1) может быть любым. Положим, что   т. е. угол а изменяется прямо пропорционально времени. Тогда (2)

Слагаемое   представляет собой действительную часть (Re) выражения  .

(3) а функция   есть коэффициент при мнимой части (Im) выражения 

(3a)

Таким образом, синусоидально изменяющийся ток I можно представить как   или, что то же самое, как проекцию вращающегося вектора   на ось +j (рис.8).

Рис.8

С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени   При этом вектор (4)

где   — комплексная величина, модуль которой равен   — угол, под которым вектор   проведен к оси +1 на комплексной плоскости, равный начальной фазе.

Величину   называют комплексной амплитудой тока i. Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени   Точка, поставленная над током  или напряжением означает, что эта величина во времени изменяется синусоидально.

Поясним сказанное. Пусть ток  Запишем выражение для комплексной амплитуды этого тока. В данном случае 

Следовательно,  Пусть комплексная амплитуда тока 

Запишем выражение для мгновенного значения этого тока.

Для перехода от комплексной амплитуды к мгновенному значению умножим   и возьмем коэффициент при мнимой части от полученного произведения :

Под комплексом действующего значения тока или комплексом тока (комплексным током)   понимают частное отделения комплексной амплитуды на