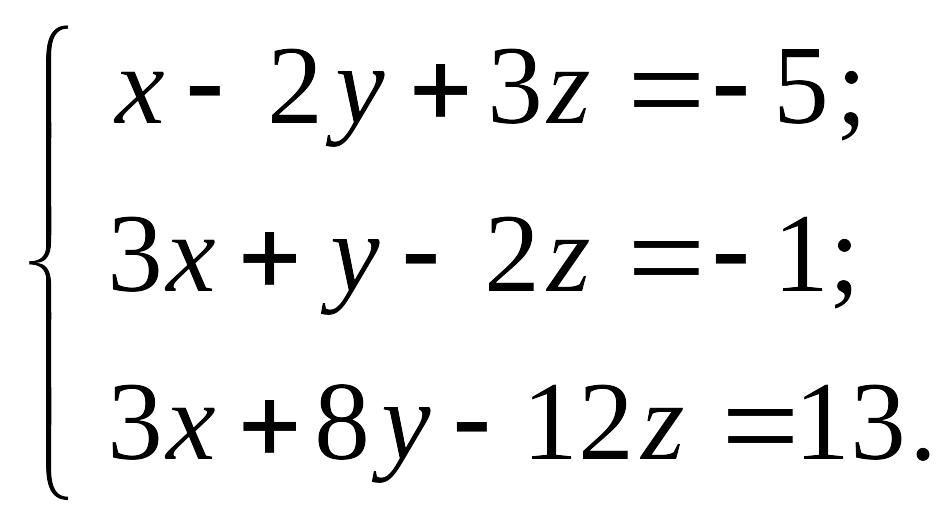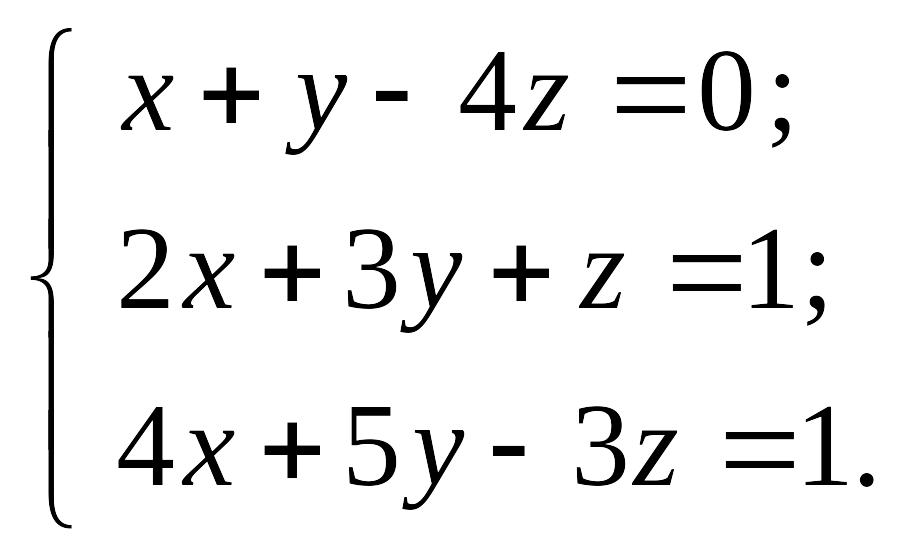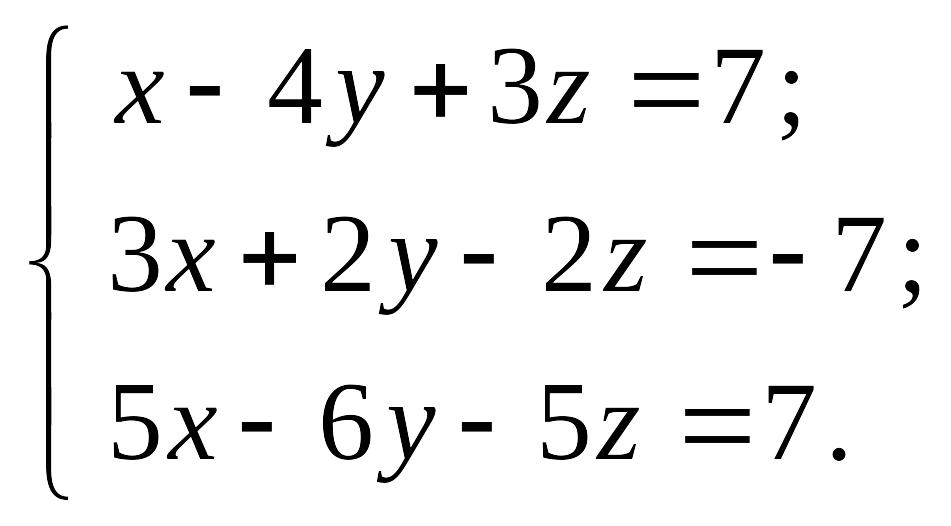- •Контрольная работа по линейной алгебре
- •Вариант № 1___Андрианова м.
- •Вариант № 2__Александрова е.
- •Вариант № 3__Ананина м.
- •Вариант № 4__Ахметова а.
- •Вариант № 5__Брюханская н.
- •Вариант № 6__Бушмелева е.
- •Вариант № 7__Владыкина м.
- •Вариант № 8__Глушков г.
- •Вариант № 9__Закирова р.
- •Вариант № 10__Кузнецова в.
- •Вариант № 11__Морозова м.
- •Вариант № 12__Нигматянова а.
- •Вариант № 13__Петрова а.
- •Вариант № 14__Петрова д.
- •Вариант № 15__Пислегина н.
- •Вариант № 16__Соколова с.
- •Вариант № 17__Трефилова а.
- •Вариант № 18__Хамидуллина а.
- •Вариант № 19__Хуснеева а.
- •Вариант № 20__Чуракова к.
- •Вариант № 21__Шевякова ю.
- •Вариант № 22__Шиляева м.
Вариант № 7__Владыкина м.
№ |
Задание |
1 |
Выполнить
действия a)
и б)
(если они возможны), где
|
2 |
Систему
уравнений записать в матричной форме
и решить её с помощью обратной матрицы,
по формулам Крамера и методом Гаусса:
|
3 |
Даны вершины
треугольника
:
а) длину стороны ; б) уравнения сторон и ; в) внутренний угол ; г) уравнение высоты ; д) координаты точки и длину высоты . |
4 |
Составить уравнение
линии, для каждой точки которой
отношение расстояний до точки
|
5 |
Даны координаты
точек
а) координаты векторов , и ; б) косинус угла между и ; в) координаты вектора векторного произведения векторов и , площадь ; г) объём тетраэдра ; д) уравнение плоскости . |
Вариант № 8__Глушков г.
№ |
Задание |
1 |
Выполнить
действия a)
и б)
(если они возможны), где
|
2 |
Систему
уравнений записать в матричной форме
и решить её с помощью обратной матрицы,
по формулам Крамера и методом Гаусса:
|
3 |
Даны вершины
треугольника
:
а) длину стороны ; б) уравнения сторон и ; в) внутренний угол ; г) уравнение высоты ; д) координаты точки и длину высоты . |
4 |
Составить уравнение
линии, для каждой точки которой
отношение расстояний до точки
и до прямой
|
5 |
Даны координаты
точек
а) координаты векторов , и ; б) косинус угла между и ; в) координаты вектора векторного произведения векторов и , площадь ; г) объём тетраэдра ; д) уравнение плоскости . |
Вариант № 9__Закирова р.
№ |
Задание |
1 |
Выполнить
действия a)
и б)
(если они возможны), где
|
2 |
Систему
уравнений записать в матричной форме
и решить её с помощью обратной матрицы,
по формулам Крамера и методом Гаусса:
|
3 |
Даны вершины
треугольника
:
,
а) длину стороны ; б) уравнения сторон и ; в) внутренний угол ; г) уравнение высоты ; д) координаты точки и длину высоты . |
4 |
Составить уравнение
линии, для каждой точки которой
отношение расстояний до точки
|
5 |
Даны координаты
точек
а) координаты векторов , и ; б) косинус угла между и ; в) координаты вектора векторного произведения векторов и , площадь ; г) объём тетраэдра ; д) уравнение плоскости . |