3.2 Уравнение диффузии и граничные условия к нему

Уравнение диффузии - дифференциальное уравнение с частными производными 2-го порядка, описывающее процесс диффузии в случае, когда перенос вещества вызван лишь градиентом его концентрации (в отличие от термодиффузии и т. п.). Д. у. чаще всего записывают в виде

где и(x, t) - концентрация вещества в точке   среды в момент времени t, D - коэф. диффузии, q - коэф. поглощения, a F- интенсивность источников вещества. Величины D, q и F обычно являются ф-циями x и t, а также могут зависеть от концентрации и(x, t). B последнем случае ур-ние (1) становится нелинейным. В анизотропной среде коэфф. диффузии D является тензорным полем.

Наиболее полно исследовано линейное Д. у., когда коэф. диффузии D и поглощения q - пост. величины. В этом случае ур-ние (1) является ур-нием параболич. типа, для к-poro в матем. физике разработаны различные методы решения: метод разделения переменных, метод источников или функций Грина (см. также Винеровский функциональный интеграл), метод интегральных преобразований и т. д. Для выделения единственного решения линейного ур-ния (1) необходимо также задать нач. и граничные условия (если диффундирующее вещество заполняет конечный объём V, огранич. боковой поверхностью S). Обычно рассматривают след. линейные граничные условия для Д. у.: 1) на границе S поддерживается заданное распределение вещества u₀(x, t):   на S поддерживается заданная плотность потока вещества, входящего в V через S:

где  - внутр. нормаль к поверхности S; 3) S полупроницаема, и диффузия во внеш. среду с заданной концентрацией и₀(x, t)через Sпроисходит по линейному закону

Простейшее Д. у.

с нач. условием   имеет решение вида

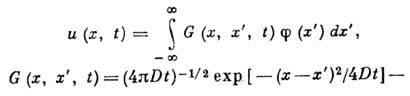
фундам. решение Д. у. (2).

Методы решения Д. у. с перем. коэф. диффузии менее развиты. В некоторых частных случаях, например, если D зависит только от концентрации u, можно аналитически найти точные решения Д. у. с перем. D.

Нелинейные матем. модели диффузии и теплопроводности (ур-ние и граничные условия) условно делят на след. классы: 1) от концентрации и зависят D или q (нелинейность 1-го рода); 2) нелинейность содержится в граничных условиях (нелинейность 2-го рода); 3) нелинейность возникает вследствие зависимости мощностей внутр. источников F от концентрации.

Одномерные нелинейные Д. у. можно решить разл. приближёнными аналитич. методами. Двухмерные и трёхмерные нелинейные Д. у. при сложной конфигурации границ области и сложных законах изменения характеристик среды, внешних и внутренних источников вещества, перем. границ области, где происходит диффузия, поддаются решению только числ. методами с применением ЭВМ. С математической точки зрения Д. у., являясь частным случаем дифференц. ур-ния, описывающего процесс установления равновесного распределения, совпадает с ур-нием теплопроводности и аналогично Навъе - Стокса уравнению для ламинарного потока несжимаемой жидкости и т. д.

3.3 Отличие загрязнений нелинейной модели от загрязнения в линейной модели

Линейная зависимость одной величины от другой — это пропорциональность их приращений, т. е. зависимость вида у = ах + b, откуда получаем ∆у = а∆x (∆ — обычное обозначение приращения), аналогично, линейная зависимость величины от двух других — это зависимость вида z = ах + by + с, откуда ∆z = а∆x + b∆у, и т. д. Типичные линейные зависимости между физическими величинами — закон Гука (удлинение пропорционально силе растяжения), закон Ома, закон теплового расширения и т. д. В действительности все эти зависимости являются линейными лишь приближенно, но в соответствующих, обычно устанавливаемых эмпирически диапазонах изменения величин предположение о линейности выполняется с хорошей точностью и в то же время существенно упрощает исследование. Любую функцию можно трактовать как преобразователь, у которого входом служит значение аргумента или набор значений аргументов, если их несколько, а выходом — значение функции. Но ведь при одинаковом наборе исходных данных, при различных видах моделирования можно получить бесконечное множество вариантов решения или аппроксимации данных. При решении задач для нахождения наиболее подходящего уравнения, описывающего зависимость полученных данных, применяется коэффициент детерминированности (коэффициент достоверности), который позволяет с определять точность зависимости найденной функции, и чем данный коэффициент ближе к 1, тем точнее уравнение описывает модель изменения данных и как следствие, тем точнее можно рассчитать последствия и пути решения множества проблем и опасностей, как загрязнения, так и других факторов, негативно влияющих на окружающую среду. Будем считать, что начала отсчета входа и выхода выбраны так, что нулевому входу отвечает нулевой выход. Тогда модель называется линейной, если в ней выполнен принцип суперпозиции (наложения), т. е. при сложении входов складываются и выходы, а при умножении входа на любое число выход умножается на то же число. Если этот принцип не выполнен, модель называется нелинейной. Линейные модели обычно описываются линейными неоднородными уравнениями — алгебраическими, дифференциальными и т. д., в которых неоднородный член отвечает входу, а решение — выходу. Так, в первом примере предыдущего абзаца при сравнительно малых прогибах модель является линейной и, приняв для определенности, что концы х = а и х = b стержня шарнирно закреплены, получаем в качестве математической модели краевую задачу (т. е. задачу о решении дифференциального уравнения при заданных краевых условиях).

Так, например, при исследовании водоемов, крайне необходимо знать структуру дна, но при линейном моделировании не всегда удается точно выявить глубинные отметки и концентрационные точки загрязнения, которые наиболее четко могут отразить нелинейные модели зависимости рельефа дня от течения и других особенностей водоема.

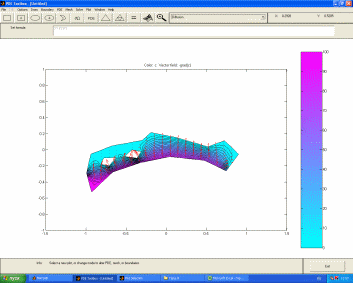
Рис. 5. Модель загрязнения водоема сточными водами в MatLab

На рисунке 3 видно направление смещения загрязняющих веществ. Программа MatLab позволяет наглядно и довольно точно определить области загрязнения, учитывая при этом направление течение водоема и ряд других особенностей при заданных условиях.

Список литературы

1. h

   ttp://bestpravo.ru/sssr/gn-postanovlenija/h6b.htm

2. http://www.water.ru/bz/param/neorg.shtml

3. http://www.ngpedia.ru/id279627p1.html

4. http://gistechnik.ru/istor-gis.html

5. http://e-lib.gasu.ru/eposobia/gis/2.html

6. http://www.fort21.ru/cont/content.php?id=689

7. http://gendocs.ru/v10294/?cc=19

8. http://kadastr.org/conf/2010/pub/infoteh/prim-surfer-ekolog.html

9. http://www.simumath.net/library/book.html?code=Ur_Mat_Ph_method_net

10. http://www.femto.com.ua/articles/part_1/1083.html