Московский технический университет связи и информатики

Кафедра автоматической электросвязи

Курсовая работа

По дисциплине: Теория телетрафика

Вариант 21

Работу выполнил

студент гр.СС0701

Толстова Т.В.

Преподаватель:

Цирик И.А.

Москва

2010г.

Содержание

1. Тема 1. Законы распределения случайных величин - 3-7 стр.

2. Тема 2. Свойство потоков вызовов. Характеристики потоков - 8-10 стр.

1. 3. Тема 3. Телефонная нагрузка, ее параметры и распределение - 10-13 стр.

4. Тема 4. Метод расчета пропускной способности однозвенных полнодоступных включений при обслуживании простейшего потока вызовов по системе с потерями. Первая формула Эрланга - 18-22 стр.

5. Тема 5. Методы расчета полнодоступных неблокируемых включений при обслуживании примитивного потока вызовов по системе с потерями. Формула Энгсета – 23-26 стр.

6. Тема 6. Методы расчета полнодоступных неблокируемых включений при обслуживании вызовов простейшего потока вызовов по системе с ожиданием - 27-30 стр.

7. Тема 8. Методы расчета пропускной способности однозвенных неполнодоступных включений: упрощенная формула Эрланга, формула О^’Делла, формула Пальма-Якобеуса - 31-37 стр.

8. Тема 9. Метод Якобеуса для расчета пропускной способности двухзвенных полнодоступных включений 38-42 стр.

9. Тема 10. Методы расчета пропускной способности двухзвенных схем, в выходы которых включен неполнодоступный пучок линий - 43-47 стр.

10. Тема 12. Метод вероятностных графов, для расчета пропускной способности, многозвенных коммутационных систем - 48-52 стр.

11. Список литературы – 53 стр.

Тема 1. Законы распределения случайных величин. Задание 1.

1. Построить распределение вероятности занятия линий в пучке из V линий в соответствии с распределениями Бернулли, Пуассона и Эрланга.

2. Для каждого распределения рассчитать математическое ожидание числа занятых линий, их дисперсию и среднеквадратическое отклонение.

Исходные данные (для варианта 21):

– вероятность занятия линии

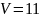– число линий в пучке

– интенсивность поступающей нагрузки

Распределение Бернулли.

Пусть исследуется пучок из V линий, каждая линия с вероятностью a может оказаться занятой и с вероятностью (1-a) – свободной. Тогда вероятность того, что в пучке из V линий окажется i любых линий занято, может быть определена из выражения:

, где i = 0, 1, …, V; Cⁱ_v = V! / i!(V – i)!

Для вычисления вероятностей P_i можно воспользоваться следующей рекуррентной формулой:

И т.д.

– математическое ожидание числа занятых линий

- дисперсия

- среднеквадратическое отклонение

Распределение Пуассона.

На оси времени на интервале [0,t) случайным образом распределяются точки – моменты поступления вызовов, в каждый из которых занимается одна из свободных линий из общего пучка линий V. Требуется найти вероятность P_i того, что на интервал [0,t) попадет точно i точек, т.е. будет занято i любых линий из V. Обозначим λ -математическое ожидание числа вызовов, приходящихся на единицу длины интервала. Обычно за единицу длины интервала времени принимается 1 час. Вероятность P_i выражается формулой:

Величина - среднее число точек, приходящихся на интервал [0,t) (математическое ожидание числа точек, попадающих на этот участок). Пусть длина интервала [0,t) равна средней длительности обслуживания одного вызова - . Величину в теории телетрафика называют интенсивностью поступающей нагрузки и обозначают A. Тогда:

,

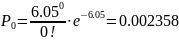
Для расчетов вероятности P_i можно использовать рекуррентную формулу:

И т.д.

Распределение Эрланга.

В теории телетрафика широко применяется усеченное распределение Пуассона, связанное с формулой Эрланга:

, i=0,1,…,V

Для определения составляющих распределения Эрланга можно применить следующее рекуррентное соотношение:

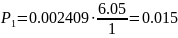
И т.д.

Таблица 1.

i	р. Бернулли	р. Пуассона	р. Эрланга
0	0.00015	0.002358	0.002409
1	0.00206	0.014	0.015
2	0.01259	0.043	0.044
3	0.04616	0.087	0.089
4	0.11284	0.132	0.134
5	0.19308	0.159	0.163
6	0.23598	0.161	0.164
7	0.20602	0.139	0.142
8	0.12589	0.105	0.107
9	0.05129	0.071	0.072
10	0.01254	0.043	0.044
11	0.00139	0.023	0.024
	0.99999	0.979	1
	6.05	6.05	5.9
	2.72	6.05	5.2