Федеральное агентство железнодорожного транспорта

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

А. С. Кухарева, Н. И. Невзоров,

Э. Д. Трощенков

Сопротивление материалов

Примеры решения задач

Часть 1

Учебное пособие

Санкт-Петербург

ПГУПС

2012

УДК 539.3/.8

ББК Ж121

К88

Р е ц е н з е н т ы:

заведующий кафедрой «Сопротивление материалов

и теория упругости» Санкт-Петербургского института

машиностроения (ЛМЗ-ВТУЗ),

доктор технических наук, профессор Е. В. Соколов;

доцент кафедры «Прочность материалов и конструкций» ПГУПС,

кандидат технических наук С. А. Видюшенков

К

К88

ухарева А. С.

Сопротивление материалов. Решение задач. Ч.1.: учеб. пособие / А. С. Кухарева, Н. И. Невзоров, Э. Д. Трощенков. – СПб. : Петербургский государственный университет путей сообщения, 2012. – с.

ISBN 978-5-7641-0330-3

Учебное пособие содержит методические указания и примеры выполнения контрольных работ по первой части курса сопротивление материалов (осевая деформация, кручение, изгиб, геометрические характеристики поперечных сечений стержней).

Предназначено для студентов заочной формы обучения.

1. Осевая деформация

(методические указания к решению задач 1,2,3)

Осевая деформация возникает при приложении к стержню нагрузок, действующих вдоль продольной оси. В частности, осевая деформация возникает в элементах шарнирно - стержневых систем. При осевой деформации из шести внутренних усилий отлична от нуля только продольная сила в стержне.

1. Определение реакций опор.

   1. Ступенчато - призматические стержни.

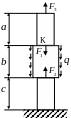
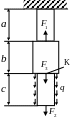
На рис.1.1. а), в) показаны схемы ступенчато - призматических стержней, нагруженных осевыми силами.

а)	б) Z	в)	г)
Рис.1.1

Реакция R, возникающая в опоре стержня, определяется из уравнения статики: сумма проекций всех сил на ось z стержня равна нулю.

Рис.1.1 б) (1.1) Рис.1.1 г) (1.2)

1.1.2. Статически определимые шарнирно - стержневые системы.

На рис.1.2 а), б) показаны схемы статически определимых шарнирно-стержневых систем.

б) a) F h2 q1 h1 α b a	q1 a b F a/2
Рис.1.2

Реакции опор в стержнях, имеющих двустороннее шарнирное прикрепление, направлены вдоль оси стержня (рис.1.3. а), б)).

h2	a b б1)
Рис.1.3

Из уравнений равновесия, записанных для опорных узлов (рис.1.3 а1) и рис.1.3 б1), б2), б3)), следует, что продольная сила в таких стержнях постоянна и равна реакции опоры

(1.3)

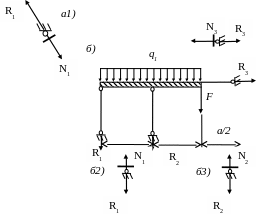
Для определения реакций опор и усилий в элементах шарнирно-стержневых систем рассматривается равновесие абсолютно жесткого диска (элемент со штриховкой) (рис.1.4, а), б)).

а )	б )
Рис.1.4

Рис.1.4 а)

(1.4)

(1.5)

(1.6)

Рис.1.4 б)

(1.7)

(1.8)

(1.9)
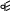
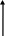