3.4 Проверка ошибок скорректированной системы
Имея все компоненты системы, определим теоретические значения ошибок. Отметим, что относительно главного входа система обладает астатизмом, поэтому постоянные входные воздействия отрабатываются с нулевой ошибкой. Однако, в системе есть возмущающее воздействие в виде сил трения, которое вносит свою долю в ошибку системы. Важно, чтобы эта доля была как можно меньше. Обычно достаточно, чтобы она не превышала
Теоретическое значение можно получить, если разрешить следующее выражение
. (3.10)
Передаточную функцию замкнутой системы по возмущению можно получить из рисунка 3.5. Перенося самый правый сумматор через два звена налево, можно получить следующую передаточную функцию (схема сворачивания показана на рисунке 3.6)
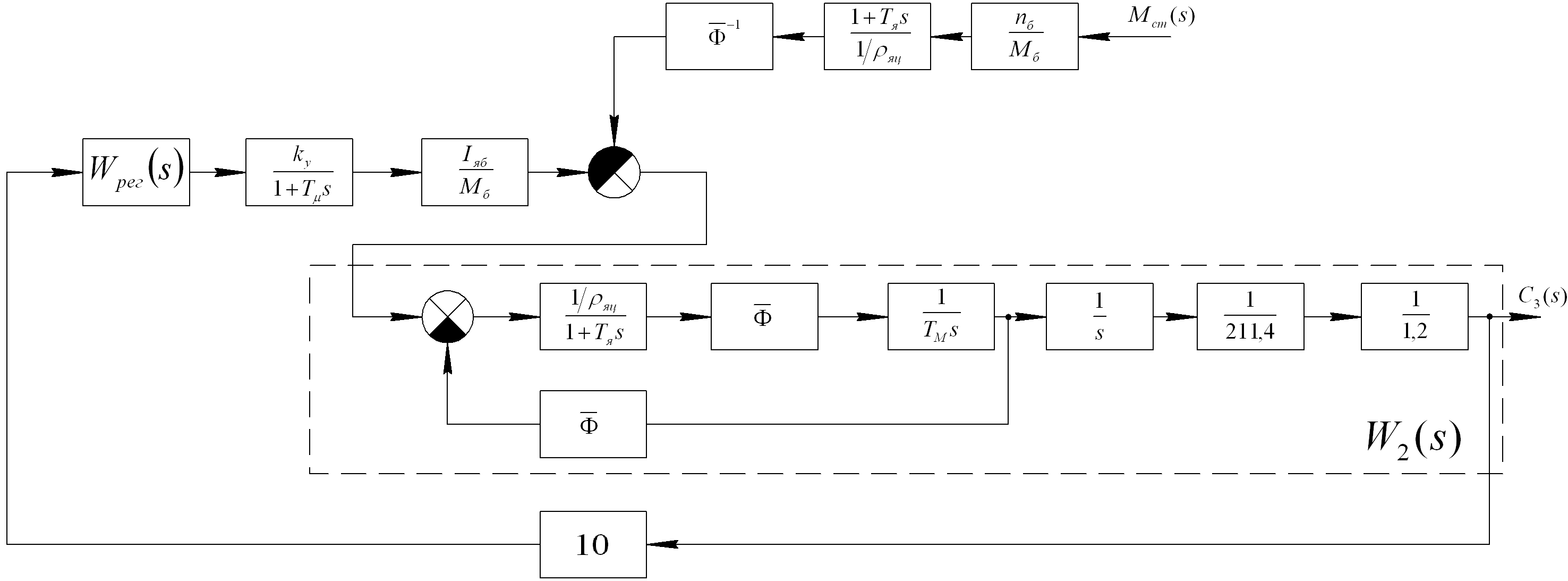
Рисунок 3.6 – Схема сворачивания для получения передаточной функции по возмущению
Разрешив предел и рассчитав (3.10) на Mathcad (Приложение А 5), получим следующие значения ошибки
Тогда,
Таким образом, доля ошибки возмущения не превышает порогового значения. Теоретическую динамическую ошибку системы можно получить, если составить частотную передаточную функцию по ошибке системы и определить ее значение на частоте контрольной точки, т.е.
, (3.11)
где 
– частотная передаточная функция
разомкнутой системы, которая получается
из (3.7).
Разрешая (3.11) в Mathcad (Приложение А 5), получим следующие значения
Не смотря на то, что полученная ошибка меньше регламента, следует помнить, что она не учитывает влияние сил сопротивления со стороны нагрузки, поэтому данное значение следует расценивать как минимальновозможное. Реальное положение дел можно узнать с помощью имитационного моделирования.
4Имитационное моделирование системы
Соберем модель скорректированной системы в системе моделирования Simulink. На рисунке 4.1 показана модель Simulink, составленная по структурной схеме рисунка 3.5.
Рисунок 4.1 – Модель Simulink
Для начала определим прямые показатели системы для краевых случаев и величину статической ошибки. Для этого следует на главный вход системы подать единичное входное воздействие. Так как обратная связь не единичная, с точки зрения системы, единичным сигналом является величина задающего воздействия Uз = 10 В.
В таблицу 4.1 сведены все интересующие нас значения. На рисунках 4.2 и 4.3 показан выход системы соответственно для минимума нагрузки и максимума нагрузки.
Таблица 4.1 – Отработка единичного входного воздействия
Случай |
Выход системы |
Прямые показатели |
εст% |
||
С3 макс, м |
С3 уст, м |
σ% |
tр (1,35%), с |
||
Минимум |
1,0750 |
0,9994 |
8 |
0,41 |
0,06 |
Максимум |
1,1566 |
0,9994 |
16 |
0,38 |
|
Рисунок 4.2 – Переходная характеристика при минимуме нагрузки
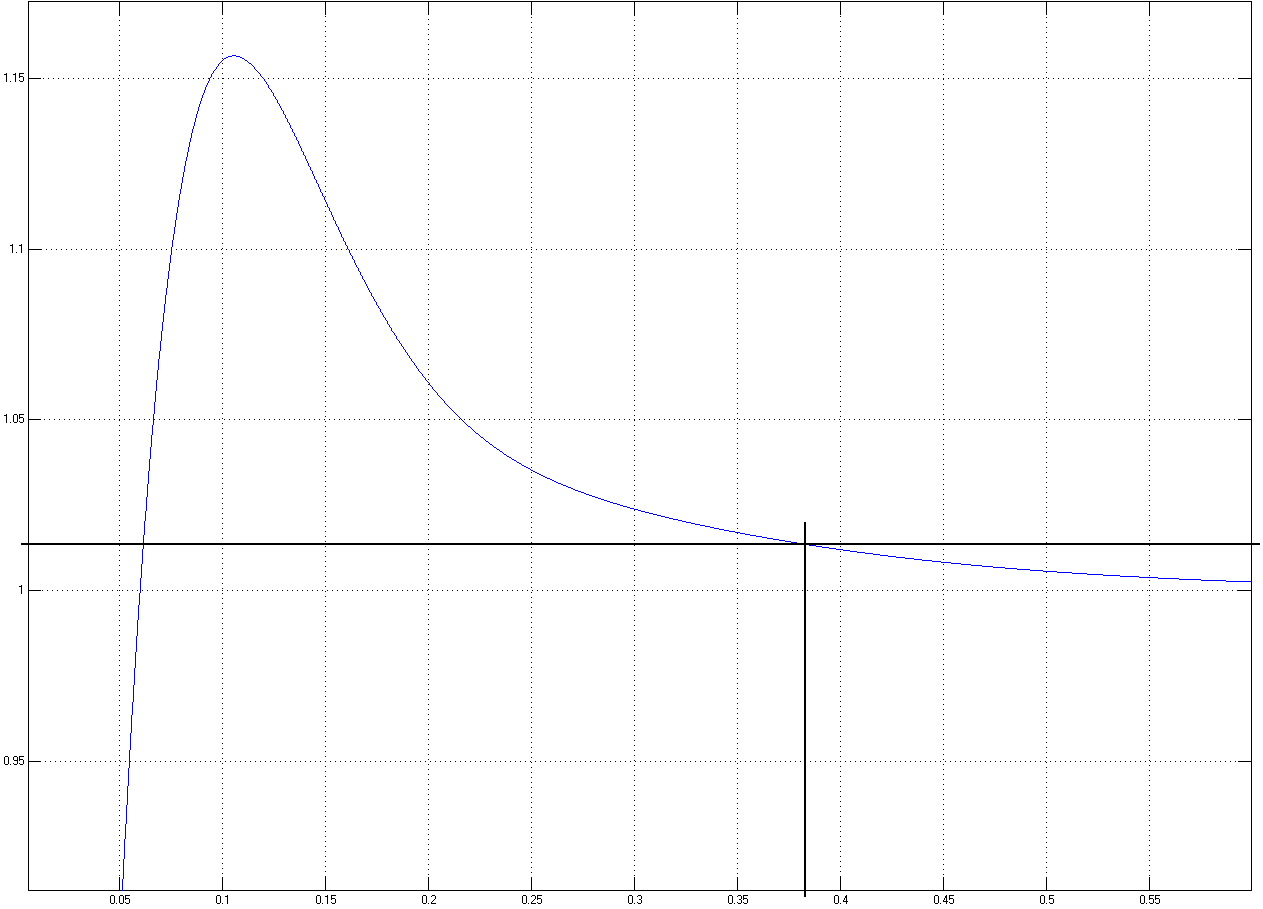
Рисунок 4.3 – Переходная характеристика при максимуме нагрузки
Очевидно, что система не выходит по прямым показателям за пределы допустимых значений. Отметим, что ненулевая статическая ошибка в данной модели полностью обусловлена возмущением и примерно совпадает с теоретическим значением.
Затем следует проверить как система отрабатывает программную траекторию. Ниже представлен код программируемого блока системы Simulink.
На рисунке 4.4 показана система после ввода программируемого блока, на рисунках 4.5 и 4.6 показан выход системы при минимуме и при максимуме нагрузки и на рисунках 4.7 и 4.8 показана ошибка системы, переведенная в относительные единицы при минимуме и при максимуме нагрузки.
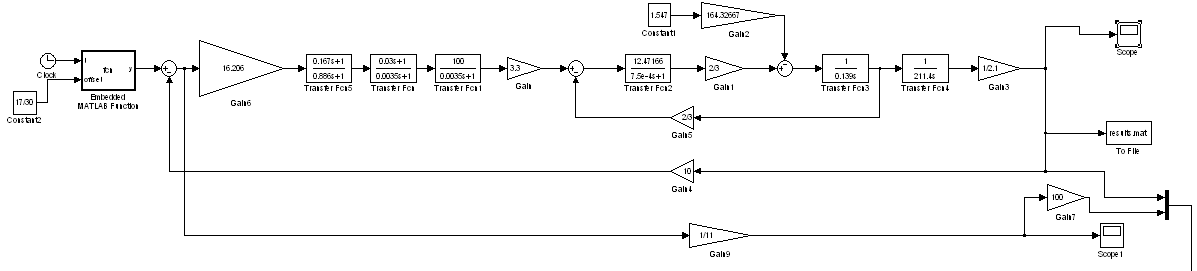
Рисунок 4.4 – Модель Simulink с введенным программируемым блоком
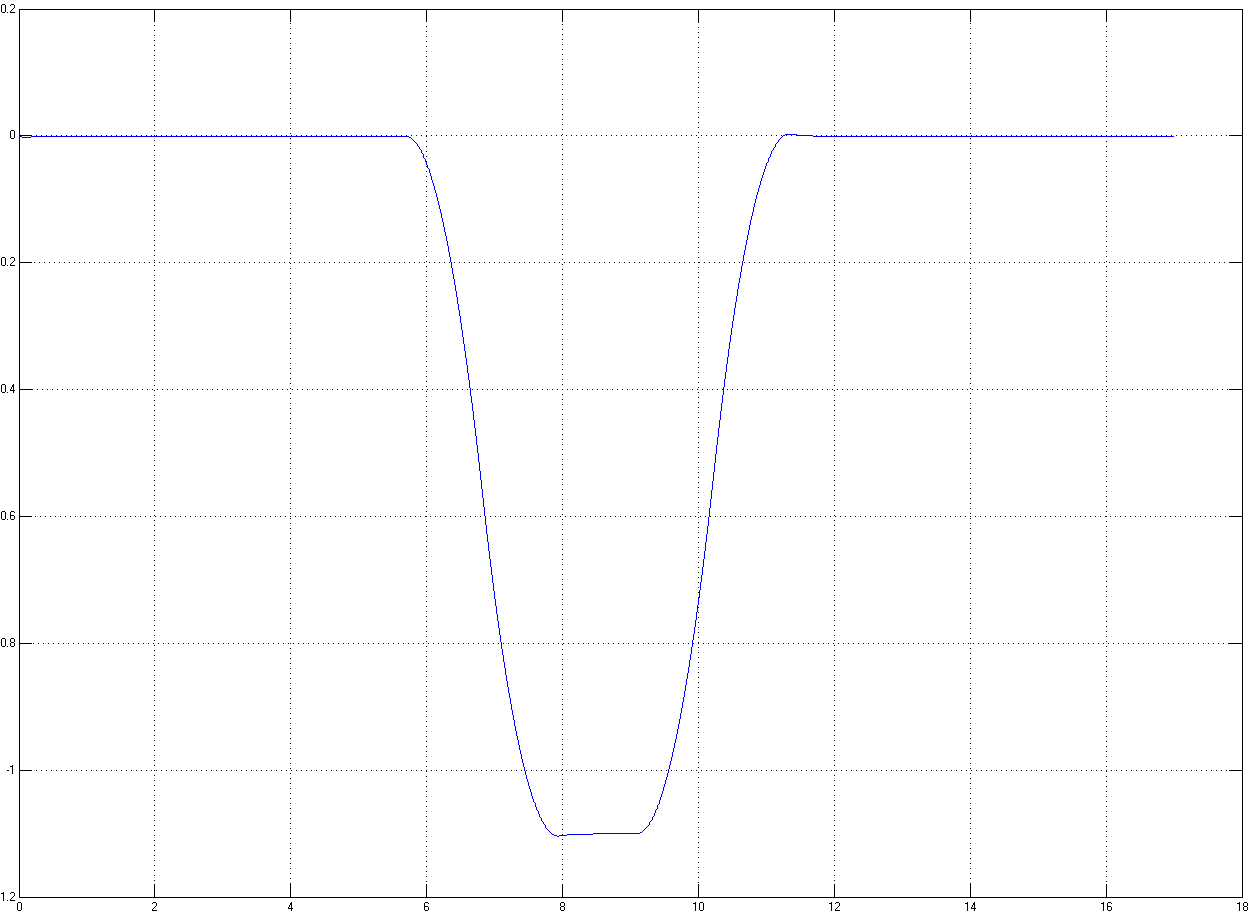
Рисунок 4.5 – Выход системы при минимуме нагрузки
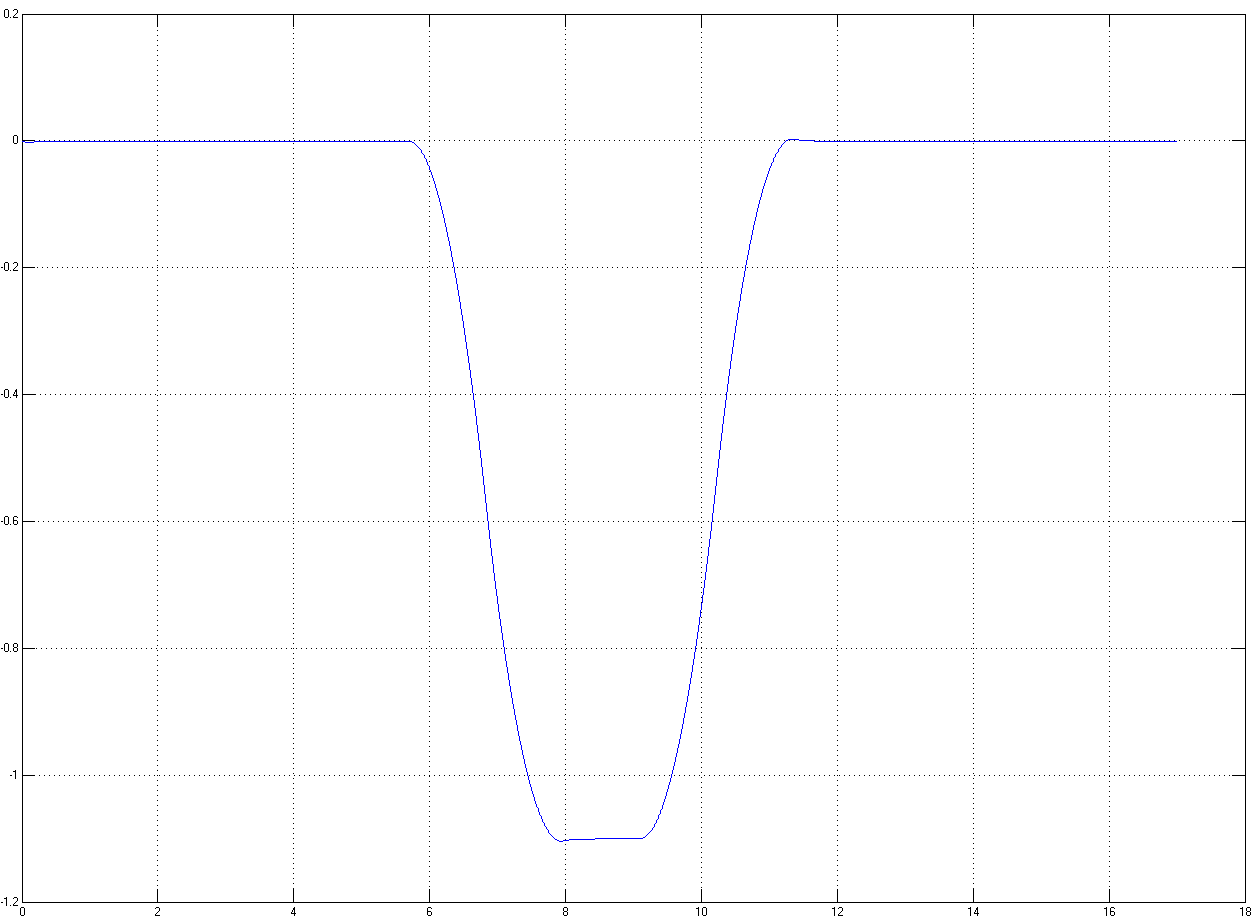
Рисунок 4.6 – Выход системы при максимуме нагрузки
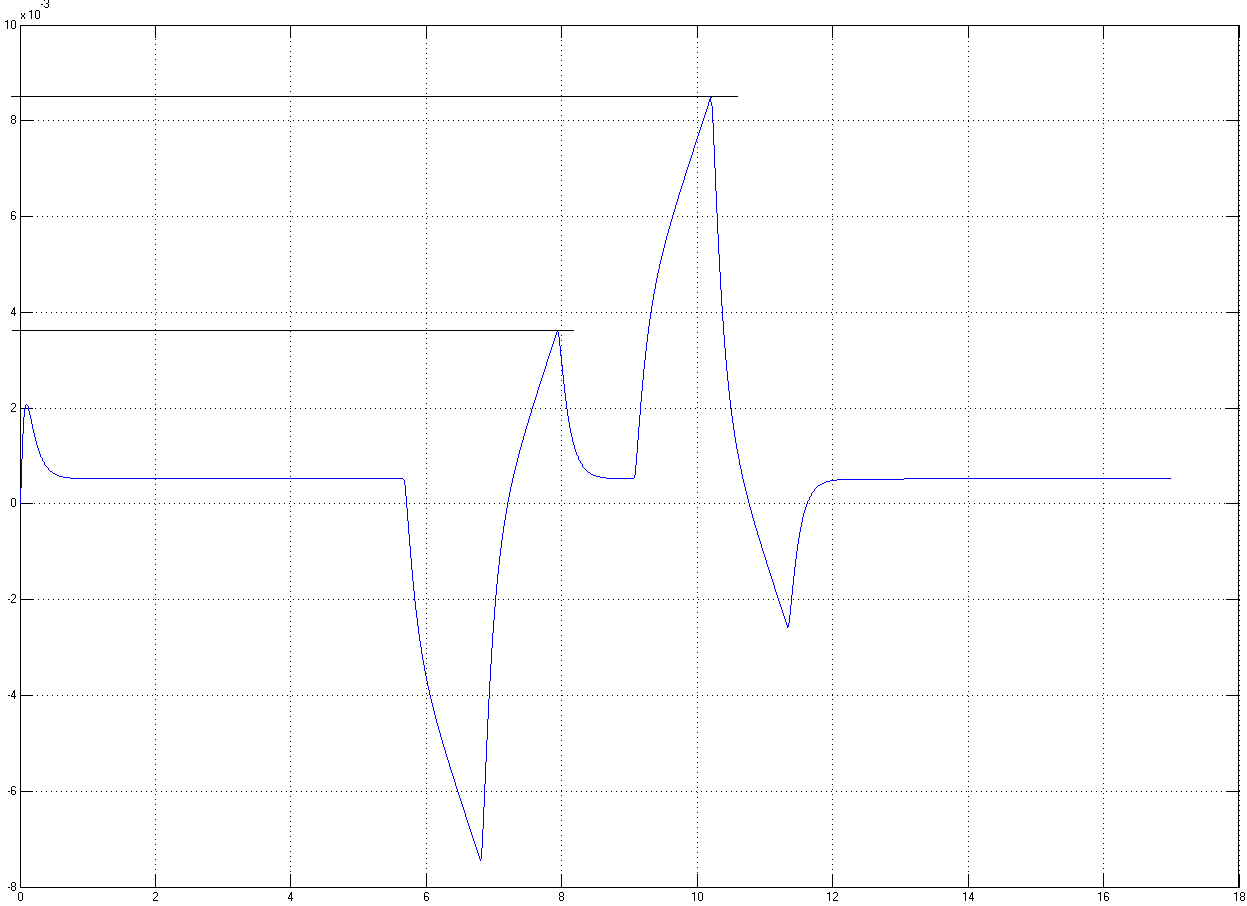
Рисунок 4.7 – Ошибка системы в относительных единицах при минимуме нагрузки
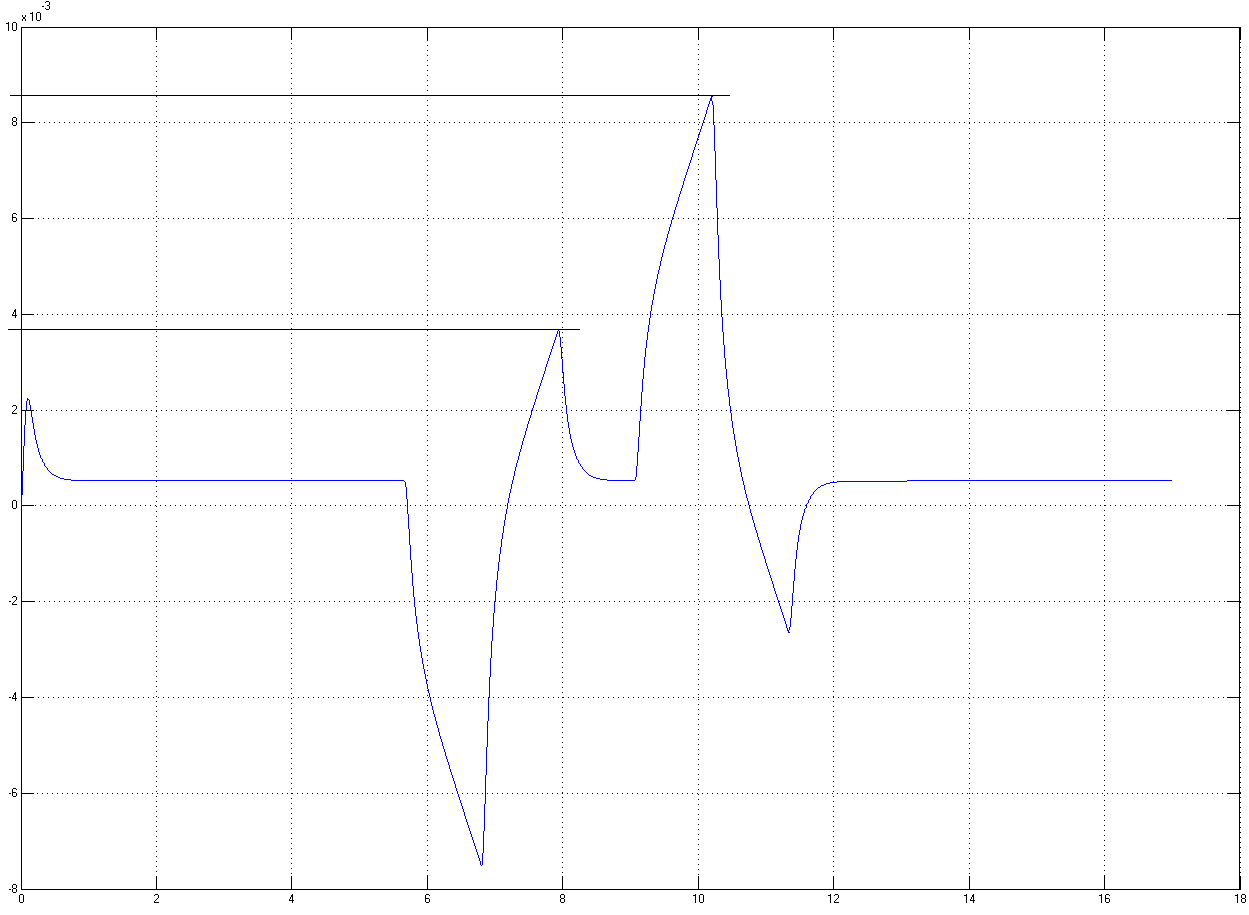
Рисунок 4.8 – Ошибка системы в относительных единицах при максимуме нагрузки
Внешне рисунки 4.5 и 4.6 достаточно хорошо повторяют рисунок 2.2, что воплощает основной замысел. По рисункам 4.7 и 4.8 можно определить максимальную динамическую ошибку системы, для чего необходимо засечь максимальный всплеск. По рисункам 4.7 и 4.8 максимальная динамическая ошибка системы равна
Отметим, что теоретическая динамическая ошибка совпадает по значению только в моменты торможения. В моменты разгона из неподвижного состояния, ошибка достигает пика и становится больше теоретического значения, но все же не превышает регламент.
Таким образом, регулятор обеспечивает заданный регламент, и нет необходимости менять его структуру.