
Тақырып: Дәрежелік қатарлар
Анықтама.
 (15)
(15)
түріндегі
функционалды қатарды дәрежелік
қатар
деп, ал
 сандары
оның коэффициенттері
деп аталады.
сандары
оның коэффициенттері
деп аталады.
Дәрежелік
қатар
 болғанда үнемі жинақты болады. Келесі
Абель теоремасы дәрежелік қатардың
жинақтылық облысын сипаттайды:
болғанда үнемі жинақты болады. Келесі
Абель теоремасы дәрежелік қатардың
жинақтылық облысын сипаттайды:
Теорема 1. (Абель теоремасы)
а) Егер
(15)
қатар
 , (
, ( )
нүктесінде жинақты болса, онда бұл қатар
)
нүктесінде жинақты болса, онда бұл қатар
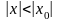 теңсіздігін қанағаттандыратын кез
келген
теңсіздігін қанағаттандыратын кез
келген
 үшін жинақты болады.
үшін жинақты болады.
б) Егер
(15)
қатар
 нүктесінде жинақсыз болса, онда бұл
қатар
нүктесінде жинақсыз болса, онда бұл
қатар
 теңсіздігін қанағаттандыратын кез
келген
үшін жинақсыз болады.
теңсіздігін қанағаттандыратын кез
келген
үшін жинақсыз болады.
Анықтама.
(15)
қатар
 интервалында
жинақты болатындай
–дің
ең үлкен мәнін осы қатардың жинақтылық
радиусы
(
интервалында
жинақты болатындай
–дің
ең үлкен мәнін осы қатардың жинақтылық
радиусы
(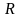 )
деп атайды, ал
)
деп атайды, ал
 интервалын жинақтылық
интервалы
деп атайды.
интервалын жинақтылық
интервалы
деп атайды.
Егер
қатар тек 0 нүктесінде ғана жинақты
болса, онда
=0
деп, ал қатар кез келген
үшін жинақты болса, онда
=
 деп санаймыз.
деп санаймыз.
жинақтылық радиусын анықтау үшін қатар жинақтылығының Даламбера және Коши белгілерінен туындайтын келесі екі формуланы қолданады:


Мысал-16.
 –қатарының
жинақтылық облысын табу керек:
–қатарының
жинақтылық облысын табу керек:
Шешуі:
 ,
,
 болғандықтан
болғандықтан

Олай
болса жинақтылық радиусы
 және жинақтылық
интервалы
және жинақтылық
интервалы
 болады. Енді жинақтылық облысын табу
үшін
болады. Енді жинақтылық облысын табу
үшін
 және
және
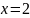 нүктелеріде берілген қатарды жинақтылыққа
зерттеу қажет:
нүктелеріде берілген қатарды жинақтылыққа
зерттеу қажет:
Егер
болса, онда
 ,
яғни қатар жинақты.
,
яғни қатар жинақты.
Егер
болса, онда
 ,
қатар жинақсыз. Сондықтан, қатардың
жинақтылық облысы
,
қатар жинақсыз. Сондықтан, қатардың
жинақтылық облысы
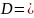 .
.
Анықтама.
 (16)
(16)
центірі нүктесіне ығысқан дәрежелік қатар деп аталады.
Егер
 айырмасын
айырмасын
 арқылы
белгілесек, онда
жинақтылық радиусын аламыз. Сондықтан,
(16)
қатардың жинақтылық интервалы
арқылы
белгілесек, онда
жинақтылық радиусын аламыз. Сондықтан,
(16)
қатардың жинақтылық интервалы
 түрінде
жазылады.
түрінде
жазылады.
Негізгі әдебиет:
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2 М.:Наука,1985г. (стр. 245-250)
Гусак А.А. Высшая математика Т.2. Мн.: Тетро Системс, 2001г. (стр. 114-119)
Бақылау сұрақтары:
1. Функционалды қатарды анықтау.
2. Жинақтылық облысы.
3. Функционалды қатардың бірқалыпты жинақтылығы.
4. Дәрежелік қатарлардың анықтамасы.
5. Дәрежелік қатарлардың жинақтылық радиусы.
6. Дәрежелік қатарлардың жинақтылық облысы.
Тақырып: Тейлор және Маклорен қатарлары
Айталық
 функциясының
нүктесі
маңында
функциясының
нүктесі
маңында
 ші
ретті туындысы бар болсын.
ші
ретті туындысы бар болсын.
Анықтама. Многочленом Тейлора го порядка функции в точке называется многочлен

(17)
өрнегін
функциясының
нүктесі маңында жазылған Тейлор
көпмүшелігі
деп атайды.
Мұнда
 =
= және 0!=1 болатыны ескерілген.
және 0!=1 болатыны ескерілген.
Анықтама.
және
 өрнектері айырмасын Тейлордың центірі
нүктесінде болатын қалдық
мүшесі
деп атайды: Оны
өрнектері айырмасын Тейлордың центірі
нүктесінде болатын қалдық
мүшесі
деп атайды: Оны
 арқылы белгілейді.
арқылы белгілейді.
(17) формуладан мына теңдіктер тізбесін аламыз:
 (18)
(18)
Жалпы
қалдық мүшенің бірнеше түрлері бар.
Солардың Лгранж түріндегі қалдық мүшесі:
 ,
мұнда
,
мұнда
 немесе
немесе
 аралықтарында
жатады.
аралықтарында
жатады.
Сонымен функциясы үшін мынадай теңдік орындалады:
 (19)
(19)
бұл өрнекті Лгранж түріндегі қалдық мүшесі бар Тейлор формуласы деп атайды.
Анықтама. Егер функциясы нүктесі маңында шексіз рет дифференциалданатын болса, онда
 (20)
(20)
өрнегін функциясын нүктесінде жазылған Тейлор қатары деп атайды.
Анықтама.
Егер
Тейлор қатарында
 деп алсақ, онда алынатын қатарды Маклорен
қатары
деп атайды.
Маклорен
қатары
былай жазылады:
деп алсақ, онда алынатын қатарды Маклорен
қатары
деп атайды.
Маклорен
қатары
былай жазылады:
 (21)
(21)
