Қатарлар теориясы Тақырып 1: Сан қатарлары

Айталық, бізге сан тізбегі берілсін. Онда келесі шексіз қосындыны қарастыралық:

(1)-ші түрдегі өрнекті сан қатары деп атайды. Мұнда сан қатарының 1-ші мүшесі, - екінші мүшесі және т.с.с. деп, ал 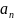сан қатарының жалпы мүшесі (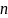 -ші мүшесі) деп аталады. Сан қатарының алғашқы мүшелерінің қосындысын қатардың дербес қосындылары деп және оны арқылы белгілейді. Мәселен,

Анықтама: Егер (1)-ші қатардың дербес қосындыларының 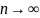болғанда шенелген шегі S бар болса, онда S саны (1)-ші қатардың қосындысы деп, ал қатардың өзін жинақты деп атайды:

Егер бұл шек анықталмаса, немесе шексіздікке тең болса, онда (1)-ші қатарды жинақсыз деп атайды.

Мысал-1: Мектеп бағдарламасында қарастырылатын қатар – геометриялық прогрессияны қарастыралық:

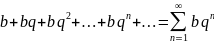
қатарын жинақтылыққа зерттеу керек. Мұнда прогрессияның алғашқы мүшесі, ал 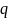оның еселігі.

Шешуі: Бұл қатардың дербес қосындылары формулаларымен анықталатынын жақсы білеміз. Осыдан

Сонымен берілген қатар 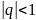болғанда ғағн шексіз кемімелі геометриялық прогрессия ретінде жинақты болатынын көреміз.

Енді қатарладың кейбір қарапайым қасиеттерін қарастыралық.

1) Егер

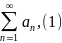
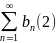
қатарлары жинақты болып, олардың қосындысы сәйкесінше және 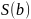болса, онда

қатары да жинақты болып, оның қосындысы санына тең.

2) Егер (1)-ші қатар жинақты болса, онда кез келген с0 саны үшін

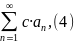
қатары да жинақты болады және оның қосындысы 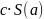санына тең.

Егер (1)-ші қатар жинақcыз болса, онда кез келген с0 саны үшін (4)-ші қатар да жинақcыз болады.

3) Егер (1)-ші қатардың санаулы мүшелерін өзгертсе, не қосымша қосып жазса, не алып тастаса, онда бұл амал қатардың жинақтылығына не жинақсыздығына әсер етпейді.

Мысал-2:

қатары жынақты (геометриялық прогрессия, еселігі ) болғандықтан, келесі қатар да жинақты болады:

Сонымен, қатардың санаулы мүшелерін өзгерту оның қосындысын өзертуі мүмкін, бірақ қатардың жинақтылығына әсер етпейді.

Теорема 1. (Қатар жинақтылығының қажетті шарты). Егер қатары жинақты болса, онда 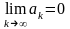теңдігі орындалады.

Дәлелдеуі: Берілген қатар жинақты болғандықтан және теңдіктері орындалады. Осыдан 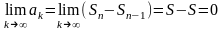теңдігін аламыз. Дәлелдеу керегі де осы.

шарты қатар жинақты болуы үшін тек қажетті шарт ғана, бірақ жеткіліксіз. Мысалы, келесі гармонкалық қатар 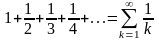жинақсыз болатыны келесі баптарда көрсетіледі. Десек те гармоникалық қатар катар жинақтылығының қажетті шартын қанағаттандырады:

.

Сонымен, қатардың жинақты-жинақсыздығын қажетті шарт көмегімен анықтау мүмкін емес. Керісінше, дәлелденген теоремаға кері тұжырым жиірек қолданылады:

Салдар. Егер болса, онда (1) қатар жинақсыз болады.

Бұл тұжырым қарсы жору тәсілімен оңай дәлелденеді.

Тақырып 2: Оң мүшелі қатарлардың жинақтылық белгілері

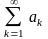Айталық, оң мүшелі қатары берілсін. Оның жинақты-жинақсыздығын зерттелік. Исследуем вопрос о его сходимости или расходимости. Так как частичные суммы ряда с неотрицательными членами образуют неубывающую последовательность, то это ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.

Приводим признаки сходимости положительных рядов.

Теорема 2. ( Салыстыру белгісі). Айталық, оң мүшелі екі қатар берілсін:

Егер шектеулі мүшелерінен өзге барлық мүшелері

(5)

Теңсіздігін қанағаттандыратын болсын. Онда (2)-ші қатардың жинақтылығынан (1)-ші қатар жинақтылығы шығады. Керісінше, егер (1)-ші қатар жинақсыз болса, онда (2)-ші қатар да жинақсыз болады.

Мысал-3.

қатарын жинақтылыққа зерттеу керек.

Шешуі: теңсіздігі орындалғаннан бастап теңсіздігі орындалады. Сондықтан, салыстыру белгісі бойынша

гармоникалық қатар жинақсыз болғандықтан берілген «үлкен» қатар да жинақсыз болады.

Әдетте, салыстыру белгілерін қолдануда геометриялық прогрессияларды және келесі Дирихле қатарларын жиі қолданады:

.

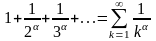Келесі баптарда Дирихле қатарының 1 болғанда жинақты, ал 1 болғанда жинақсыз екенін көрссетеміз. Мысалы, =1 болғанда Дирихле қатары гармоникалық қатарды беретінін көреміз.

Мысал-4. - қатарының жинақтылығын анықталық.

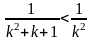Шешуі: Бұл қатармен салыстыру үшін жинақты Дирихле қатарын қолданамыз. Мұнда =21. Кез келген үшін орындалатын теңсіздігінен теңсіздігі орындалатыны шығады. Олай болса берілген «кіші» қатар да жинақты болады.

Шектік салыстыру белгісі:

Егер оң мүшелі (1) және (2) қатарлары үшін 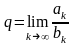, , теңдігі орындалса, онда бұл қатарлардың екеуі бірдей жинақты, немесе екеуі бірдей жинақсыз болады.

Мысал-5. - қатарының жинақтылығын анықталық.

Шешуі: Берілген қатардың жалпы мүшесінің алымында да, бөлімінде де -ның ең үлкен дәрежесін қалдырып, салыстыруға арналған қатардың жалпы мүшесін аламыз: . Бұл мүшелер дәреже көрсеткіші =4/31 болатын және сондықтан жинақты Дирихле қатарын береді. Енді шектік салыстыру белгісіндегі санын анықталық:

Сонымен, шектік салыстыру белгісі бойынша берілген қатар жинақты.

Теорема 3. (Даламбер белгісі)

Айталық оң мүшелі қатары үшін

, (6)

шегін анықталық:

а) егер болса, онда берілген қатар жинақты болады;

б) егер 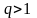немесе 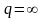болса, онда бұл қатар жинақсыз болады;

в) егер 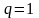болса, онда берілген қатардың жинақтылығы не жинақсыздығы белгісіз, яғни Даламбер белгісі қолданылмйды.

Даламбер белгісін қатардың жалпы мүшесі -ға тәуелді факториал және көрсеткіштік өрнектерден құралған жағдайларда қолданған ыңғайлы.

Мысал-6. 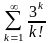- қатарының жинақтылығын анықталық.

Шешуі: Бұл қатарда 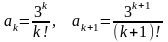, сондықтан,

,

яғни болғандықтан берілген қатар жинақты.

Теорема 4. (Кошидің радикалдық белгісі). Айталық оң мүшелі қатары үшін

(7)

шегін анықталық:

а) егер болса, онда берілген қатар жинақты болады;

б) егер немесе болса, онда бұл қатар жинақсыз болады;

в) егер болса, онда берілген қатардың жинақтылығы не жинақсыздығы белгісіз, яғни Кошидің радикалдық белгісі қолданылмйды.

Кошидің радикалдық белгісі 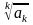түбірі алынатын жағдайларда қолданылады.

Мысал-7. - қатарының жинақтылығын анықталық.

Шешуі: . Сонымен, 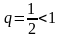болғандықтан берілген қатар жинақты.

Рис. 1

Теорема 5. (Кошидің интегралдық белгісі).

Айталық оң мүшелі қатары берілсін және 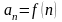, - теріс емес аралығында бірсарында кемімелі функция болсын. Онда қатары жинақты (жинақсыз) болуы үшін

(8)

меншіксіз интегралының жинақты (жинақсыз) болуы қажетті және жеткілікті.

Айталық қатары жинақты және оның қосындысы 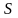–ке тең болсын, онда геометриялық тұрғыдан дербес қосындыларының мағынасы табаны 1-ге, ал биіктігі болатын тіктөртбұрыштар аудандарының қосындысына тең (сурет-1).

Мысал-8. - Дирихле қатарының жинақтылығын анықталық.

Шешуі: -функциясын қарастыралық. Мұнда мен х орындарын алмастырсақ, онда 0 болғанда бұл функция Теорема-5 шарттарын толық қанағаттандырады. Функция аралығында үздіксіз және кемімелі болады.

Айталық, 1 болсын, онда , яғни 1 болғанда Дирихле қатары жинақты болады.

1 болсын, онда яғни 1 болғанда Дирихле қатары жинақсыз болады.

=1 болсын, онда 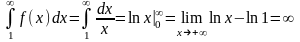, яғни =1 болғанда Дирихле қатары (гармоникалық қатар) жинақсыз болады.

Мысал-9. 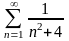-қатарының жинақтылығын анықталық.

Шешуі: Әрине бұл қатардың жинақтылығын Дирихле қатарымен салыстыру арқылы анықтауға болады. Десек те бұл жәйтті Кошидің интегралдық белгісімен анықталық. Ол үшін (0;+) аралығында бірсарынды кемімелі функциясын қарастыралық. Онда

Сондықтан берілген қатар жинақты

Негізгі әдебиет:

1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2 М.:Наука,1985г. (стр. 245-250)

2. Гусак А.А. Высшая математика Т.2. Мн.: Тетро Системс, 2001г. (стр. 114-119)

Бақылау сұрақтары:

1. Сан қатарының анықтамасын беріңдер.

2. Сан қатарының жинақтылығы мен жинақсыздығы.

3. Жинақты қатар қасиеттері.

4. Қатар жинақтылығының қажетті шарты.

5. Оң мүшелі қатарлар.

6. Салыстыру белгісі.

7. Шектік салыстыру белгісі.

8. Даламбер белгісі.

9. Кошидің радикалдық белгісі.

10. Кошидің интегралдық белгісі.

Тақырып: Таңбасы ауыспалы қатарлар. Абсолютты және шартты жинақты қатарлар

Анықтама.

(9)

түріндегі қатарлар таңбасы ауыспалы қатар деп атайды, мұнда , .

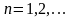Для исследования сходимости таких рядов используется следующий признак.

Теорема 7 (Лейбниц белгісі). Айталық (9) таңбасы ауыспалы қатар келесі екі шартты қанағаттандырсын: а) ; б)   сан тізбегі кемімелі, яғни 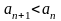,  . Онда (9) қатр жинақты болады және оның қосындысы мына теңсіздікті қанағаттандырады:

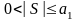
Мысал-10. -таңбасы ауыспалы қатардың жинақтылығын анықталық.

Шешуі: 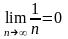және кез келген үшін теңсіздігі орындалады. Яғни Лейбниц белгісі бойынша берілген қатар жинақты және оның қосындысы теңсіздігін қанағаттандырады.

Келесі қатарларды қарастыралық:

(10)

. (11)

Анықтама. Егер (11) қатар жинақты болса, онда (10) қатар абсолютты жинақты деп, ал егер (11) қатар жинақсыз болып, (10) қатар жинақты болса, онда (10) қатарды шартты жинақты деп атайды.

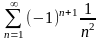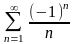Мысалы, қатары абсолютты жинақты себебі қатары жинақты. –қатары шартты жинақты (10-мысал), себебі 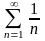гармоникалық қатарының жинақсыз екенін жақсы білеміз.

Негізгі әдебиет:

1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т.2 М.:Наука,1985г. (стр. 245-250)

2. Гусак А.А. Высшая математика Т.2. Мн.: Тетро Системс, 2001г. (стр. 114-119)

Бақылау сұрақтары:

1. Сан қатарының анықтамасын беріңдер.

2. Сан қатарының жинақтылығы мен жинақсыздығы.

3. Жинақты қатар қасиеттері.

4. Қатар жинақтылығының қажетті шарты.

5. Оң мүшелі қатарлар.

6. Салыстыру белгісі.

7. Шектік салыстыру белгісі.

8. Даламбер белгісі.

9. Кошидің радикалдық белгісі.

10. Кошидің интегралдық белгісі.

11) Таңбасы ауыспалы қатар анықтамасы.

12) Таңбасы ауыспалы қатар жинақтылығының Лейбниц белгісі.

13) Абсолютты және шартты жинақты қатарлар.

14) Абсолютты жинақтылық белгісі.