Р. Є. БУБЛЕЙ, Є. М. БУБЛЕЙ

Фізичний

ПРАКТИКУМ

ДЛЯ ПІДГОТОВЧИХ ВІДДІЛЕНЬ

Допущено Міністерством вищої і середньої спеціальної освіти УРСР як навчальний по­сібник для слухачів підготовчих відділень вузів

ВИДАВНИЧЕ ОБ’ЄДНАННЯ «ВИЩА ШКОЛА>> ГОЛОВНЕ ВИДАВНИЦТВО КИЇВ — 1974

53

Б90

УДК 53 (076.5)-

Физический практикум. Для подготовительных отделений. Б у б л е й Р. E., Б у б л е й E. Н. Издательское объединение «Вища школа», 1974, 112 с. (на украинском языке).

Цель пособия — на небольшом количестве ла­бораторных работ (20) закрепить основные идеи и законы физики, которые изучались в школе. Практикум написан с учетом новых программ. Все величины даны в Международной системе единиц (СИ). Работы описаны достаточно подробно, поэтому их можно выполнять как после повторения всего курса, так и после изучения отдельных тем. Боль­шое внимание уделено изложению основ теории ошибок, иллюстрации ее применений.

Пособие предназначено для слушателей под­готовительных отделений вузов. Его можно также использовать для проведения лабораторных работ в средних школах и техникумах.

Табл. 18. Ил. 56. Библиогр. 4.

Редакція літератури з математики і фізики Зав. редакцією А. С. Макуха

Видавниче об’єднання «Вища школа», 1974.

Передмова

Викладання фізики на підготовчих від­діленнях вузів має своїм завданням не тільки повторення загальнообов’язкової програми середньої школи, а й створення фундаменту для осмисленого і глибокого засвоєння слухачами загальноосвітніх і спеціальних дисциплін вузу. При стислих строках повторення курсу фізики доцільно приділити більше уваги теорії і лекційним демонстраціям, а практикум провести в кін­ці курсу на невеликій кількості добре про­думаних лабораторних робіт, що містять відомості з різних розділів. Така форма проведення практикуму, як показує досвід, дає змогу слухачам виконати лабораторні роботи на високому рівні, ще раз і більш ефективно повторити й засвоїти теоретич­ний курс.

Важливим елементом практикуму є ви­ховання вдумливого ставлення до виконан­ня і результатів експерименту. Тому авто­ри вважали за доцільне ввести в посібник основи теорії похибок. Положення теорії проілюстровано прикладами.

Проведенню лабораторних робіт повин­но передувати вступне заняття, на якому слухачів ознайомлюють з правилами пове­дінки в лабораторії, технікою вимірювань, обробкою результатів і обчисленням похи­бок. Кожна лабораторна робота розрахо­вана на дві години. Щоб забезпечити само­контроль підготовленості до виконання ро­боти, до кожного завдання розроблено кон­трольні запитання.

Для кращої підготовки до виконання ла­бораторних робіт у кінці кожної з них на­ведено два варіанти потрібної літератури.

Посібник підготовлено як підсумовую­чий практикум для виконання після ви­вчення всього теоретичного курсу. Досить докладний опис робіт дає можливість вико­ристати його на підготовчих відділеннях вузів, у середніх школах і технікумах для проведення лабораторних робіт "протягом навчального року.

Автори висловлюють подяку В. Г. Чепуренку, 3. П. Двоскіну і А. І. Бублей за перегляд рукопису і конкретні поради.

Зауваження щодо поліпшення якості посібника надсилати на адресу: 252054, Київ, 54, Гоголівська, 7, Головне видавниц­тво видавничого об’єднання «Вища школа», редакція літератури з математики і фізики.

Автори

Розділ І

ВИМІРЮВАННЯ І ОБРОБКА ЇХ РЕЗУЛЬТАТІВ

Фізика стала наукою з того часу, коли її основним ме­тодом пізнання став експеримент. При його виконанні про­водяться вимірювання, тобто визначення, у скільки разів вимірювана величина більша чи менша за величину, узяту за одиницю.

Ніяке вимірювання не можна виконати абсолютно точно. Тому результатом будь-якого вимірювання є наближене число, величина якого тим ближча до справжнього значен­ня, чим менша похибка. Знаходження похибки вимірювання дає змогу встановити границі існування шуканої величини. Наприклад, вимірюванням установлено, що “довжина тіла l= 0,453 м, а похибка становить ±0,001 м. Це означає, що шукана величина обмежена границями 0,452 м < / < 0,454 м. Таким чином, зазначення похибки вимірювання значною мірою компенсує неможливість установлення точ­ного значення величини.

Виміряти яку-небудь величину — це означає визначити результат вимірювання й похибку, допущену при його знаходженні. Вимірювання можуть бути безпосередніми і посередніми.

§ 1. Похибки безпосередніх вимірювань

При безпосередньому вимірюванні числове значення ве­личини знаходять внаслідок безпосереднього порівняння її з одиницею вимірювання за допомогою приладів. Так, на­приклад, довжину вимірюють за допомогою метра, тиск — за допомогою манометра і т. п. Похибки при вимірюваннях бувають систематичні і випадкові.

Систематичні похибки виникають від користування не­справними або неправильно встановленими приладами, внаслідок недосконалості методів вимірювань і обчислена. Характерною особливістю таких похибок є їх обов’язкова повторюваність при кожному вимірюванні. Так, систематично повторюватиметься похибка при вимірюванні довжини урізаним метром, при вимірюванні сили струму амперметра з викривленою стрілкою, температури — за зміщеною шкaлою термометра та ін. Систематичні похибки можна вияви­ти і врахувати.

Випадкові похибки виникають незалежно від дослідни­ка з різних причин. Наприклад, під час вимірювань може непомітно зміститись око спостерігача або повітряна течії може змістити стрілку приладу. Передбачити й усунути тaкі похибки неможливо. Треба навчитися знаходити їх i враховувати.

Ознайомимося з властивостями і методами знаходження випадкових похибок. Позначимо результати п окремих ви- мірювань шуканої величини А через а_1, а₂,…. а_п. Харак­терною особливістю випадкових похибок є те, що при ба­гаторазових вимірюваннях похибки однакової величини н бік збільшень або зменшень зустрічаються однаково часто. Тому загальна алгебраїчна сума випадкових похибок при багаторазових вимірюваннях величини А дорівнюватиме нулю, а середнє арифметичне значення а результатів n ви­мірювань

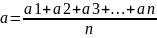
при великому n буде близьке до істинного значення А. Це середнє значення а і беруть за результат вимірювання. Різницю між середнім значенням величини і результатом окремого вимірювання називатимемо похибкою цього ви­мірювання. Так, похибка першого вимірювання ∆а_х = а — — а₁, похибка другого ∆а₂ — а — а₂, похибка n-го ¹ ви­мірювання ∆а_n = а — а_п.

Середнє арифметичне з n абсолютних значень виявлених похибок дає середню похибку, або похибку результату:

____________

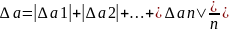
Вираз ∆а_n = а — а_n точніше слід було б називати практично ви­значуваною похибкою, на відміну від істинної похибки ∆а_n = А — а_n, яка нам невідома, бо невідоме істинне значення А. Пам’ятаючи де, за­лишимо все ж за ∆а_n назву похибки для зручності.

____________

Виміряти яку-небудь величину А — це означає знайти її середнє значення а і середню похибку ∆а. Тому

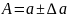
Написання двох знаків (±) перед середньою похибкою по­казує, що шукана величина обмежена границями (а + ∆а) > А > (а — ∆а).

Для порівняння точності різних вимірювань ще не до­сить визначити похибку. Справді, якщо результат вимірю­вання довжини одного тіла 0,010 ± 0,005 м, а другого — 1,000 ± 0,005 м, то хоч похибки в обох випадках і однако­ві, проте друге тіло виміряне значно точніше (0,005 м від їм становить усього 0,5%, а 0,005 м від0,01м — 50%). Для порівняння точності вимірювань користуються понят­тям відносної похибки. Відносною похибкою є називають відношення середньої похибки ∆а_n до середнього значення величини а:

Звичайно відносну похибку визначають у процентах.

У розглянутому вище прикладі порівняння точності ви­мірювань 0,010 м і 1 м відносна похибка буде відповідно:

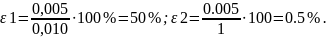
Порівняння відносних похибок виразно показує, що 1 м виміряно з точністю в 100 раз більшою, ніж 0,01 м.

Похибки числових значень величин, узятих з довідко­вих таблиць, при відсутності достатніх даних беруть такими, що дорівнюють половині одиниці останнього розряду, а при наявності даних розраховують.

Приклад. Визначити похибку і відносну похибку числа 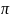= 3,1416 при обмеженні двома знаками після коми.

Беручи значення = 3,1416 за точне, а 3,14 — за наближене, дістаємо похибку ∆ = 3,1416 — 3,14 = 0,0016 »

=0,002 і відносну похибку = 100% = 0,06%.

Інколи при вимірюваннях допускають промахи — похиб­ки великої величини, що спотворюють результати. Вони виникають внаслідок недбалості, недосвідченості або вто­ми експериментатора. їх відкидають як помилкові.