2.4. Метод штрафных функций

Суть метода заключается в преобразовании исходной целевой функции посредством включения в нее функции от ограничений, получая, таким образом, задачу безусловной оптимизации [5, 21], для решения которой можно использовать рассмотренные в первой части методы. Переход от задачи условной оптимизации к задаче безусловной оптимизации осуществляется посредством включения в исходную функцию “штрафов” за нарушение ограничений задачи. Если исходная задача имеет следующий вид:

max f(x),

xRN при ограничениях:

gj (x) ≥ 0 (j = 1,...,J) hk(x) = 0, (k = 1,...,K)

то преобразованная задача определится как:

P(x,R) = f(x) + [R,h(x),g(x)]

где  - штрафная функция от ограничений задачи, а R - штрафной параметр. Наличие штрафного параметра R вызвано тем, что введение штрафной функции сильно деформирует поверхность целевой функции, что, в свою очередь, приводит к ухудшению обусловленности преобразованной задачи. Поэтому параметр R служит “регулятором” веса штрафной составляющей в целевой функции, и процесс решения задачи разбивается на ряд вспомогательных задач с различными значениями параметра R и контролем сходимости их решений.

Наиболее распространенными являются следующие виды штрафов: квадратичный, логарифмический, штраф, заданный обратной функцией, штраф типа квадрата срезки.

Квадратичный штраф используется для учета ограничений-равенств и имеет вид: F(R, h(x)) = R(h(x))².

Его значение резко возрастает при отклонении h(x) от нуля, однако, стационарная точка штрафной функции P(x,R) стремится к х* – стационарной точке исходной функции.

2.5. Алгоритм метода штрафных функций

Шаг 1. Задать: начальную точку х⁽⁰⁾, исходный штрафной параметр R⁽⁰⁾, погрешность решения.

Шаг 2. Определить штрафную функцию для R^(k) и найти точку ее экстремума x^(k).

Шаг 3. Изменить значение штрафного параметра

Шаг 4. Достаточно ли близка x^(k) к х* ?

Да: закончить процесс;

Нет: перейти к шагу 2.

2.6. Оптимизация параметров системы среднего калибра с присоединенной камерой подгона

Одной из схем, способных проводить модернизацию классического орудия без изменения внутренних геометрических параметров его ствола, обеспечивая при этом новый принцип дополнительного подгона снаряда, является схема с ускоряемыми камерами подгона Сафронов А.И., Крайнов А.Ю. Внутренняя баллистика установки среднего калибра // Вестник ТГПУ. 2004. №6. С. 173–179.

На рис. 1.1. изображён продольный разрез артиллерийской системы СПК. Процесс выстрела в модернизированном орудии будет протекать в соответствии с описанием процесса выстрела СПК данным в подразделе 1.2.

В данной главе приведено описание метода решения обратной задачи внутренней баллистики СПК, опирающееся на газодинамическую модель и методы нелинейного программирования.

Эффективность предлагаемого подхода показана на примере проектирования 125-мм установки СПК с использованием штатных порохов.

В данных системах существенное влияние на показатели выстрела оказывают волновые эффекты в газах, поэтому расчёт внутрибаллистических характеристик и определение оптимальных условий заряжания для СПК необходимо проводить по газодинамической модели. Решение ПЗВБ подобных систем проводится на основе модели газопороховой смеси. Особенности задачи учитываются при использовании комбинированной системы координат, индивидуальной для каждой из расчётных областей и связанной с левой границей соответствующей области (см. рис. 1.2.).

Практически классическая схема выстрела позволяет метать из ПБУ с длинным стволом относительно тяжёлые снаряды с коэффициентом относительного веса Cq = 2 (кг/дм³) со скоростями около 2200 м/с при максимальных давлениях на дно канала до 500 МПа.

Таким образом, при ограничении максимальных давлений на дно канала до 1000 … 1200 МПа классическая схема выстрела не в состоянии обеспечить достижение скоростей метания относительно тяжёлых снарядов в диапазоне 2500 … 3000 м/с на системах с ограниченной длиной ствола.

В случае применения СПК для метания относительно тяжёлых ПЭ с Cq = 2,7 (кг/дм³) были получены скорости 2620 м/с. В связи с этими данными, представляет интерес реализация подобных скоростей метания на установках СПК среднего и малого калибров с ограниченной длиной ствола.

Учитывая ограничение длины ствола, целесообразно повысить давление в стволе и на дне канала рассматриваемых установок. Предполагалось, что максимальное давление на дно канала установки калибра 125 мм ограничено 1200 МПа, в области дополнительного заряда считалось допустимым давление 1000 МПа.

Для артиллерийской установки калибра 125 мм был выбран объём каморы равный 34 дм³, а длина ствола считалась равной 6,1 м, масса снаряда составляла 5,9 кг (Cq = 3 кг/дм³).

Для практики, в том числе и для модернизации существующих артиллерийских систем, представляет интерес задача определения параметров СПК в рамках фиксированной геометрии, поэтому при оптимальном внутрибаллистическом проектировании варьируем только условия заряжания и параметры схемы.

Требуется максимизировать скорость снаряда

UД  max

(2.5)

при ограничении на допустимые давления в основной камере, на правой границе поршня схемы и на снаряде

		(2.6)

где р₀ – давление на дно канала ствола.

В качестве варьируемых параметров выберем величины

=

(2.7)

где ₁, ₂ – масса основного и дополнительного зарядов;

I_k1, I_k2 – импульс пороха основного и дополнительного зарядов;

t_З – время задержки зажигания;

h₁, h₂, h₃, h₄ – ограничения по давлениям на соответствующих границах расчётных областей.

Варьирование параметров (2.7) проводим в области, определяемой ограничениями вида

(2.8)

где – нижняя и верхняя границы, определяемые из физических соображений.

Для нахождения максимума (2.5) при ограничениях (2.6), определяемых на решениях системы (1.1) с граничными условиями (1.2), применяются поисковые методы нелинейного программирования, при этом нелинейные ограничения (2.6) учитываются с помощью квадратичной штрафной функции, линейные ограничения (2.8)  с помощью проектирования, а последовательность задач по максимизации штрафной функции вида

F=U_Д – ,

где К_i – штрафные множители

– с применением Р – точечных алгоритмов оптимизации, не использующих в процессе поиска производные.

Увеличивая К_i мы последовательно добиваемся более точного выполнения ограничений (2.6).

В качестве примера в таблице 2.2 приведены значения управляющих параметров и показателей процесса выстрела при оптимизации модельной артиллерийской системы СПК калибра 125 мм. Показан вариант заряжания с параметрами х₀, удовлетворяющий ограничениям (4.8) и показывающий существенную чувствительность процесса к неоптимальному выбору х.

Результаты предварительного подбора параметров х_i приняты за начальное приближение для последующей оптимизации. Соответствующие расчётные баллистические параметры начальной точки приведены на рис. 2.2,а.

Таблица 2.1. Оптимизация параметров системы нетрадиционной схемы

Управляющие пара метры и показатели процесса	хН	хВ	х1	х0	х*
	Калибр 0,125 м; Cq =3 кГ/дм3
Параметры:
1, кг	15	32	28,86	29,05	31,99
2, кг	4	7	5,44	4,54	5,44
Ik1, МПа·с	0,1	2,5	1,881	1,895	2,049
Ik2, МПа·с	0,08	1,0	0,540	0,559	0,504
QГ, кг	1,0	10	4,25	3,06	1,51
tЗ, мс	1,0	10	4,92	4,03	4,17
Показатели:
UД, м/с			2644	2379	2830
max p0, МПа	1200	1200	1107	953	1249
max p1, МПа	1000	1000	783	687	928
max p2, МПа	1000	1000	763	499	826
max p3, МПа	1000	1000	873	510	1051

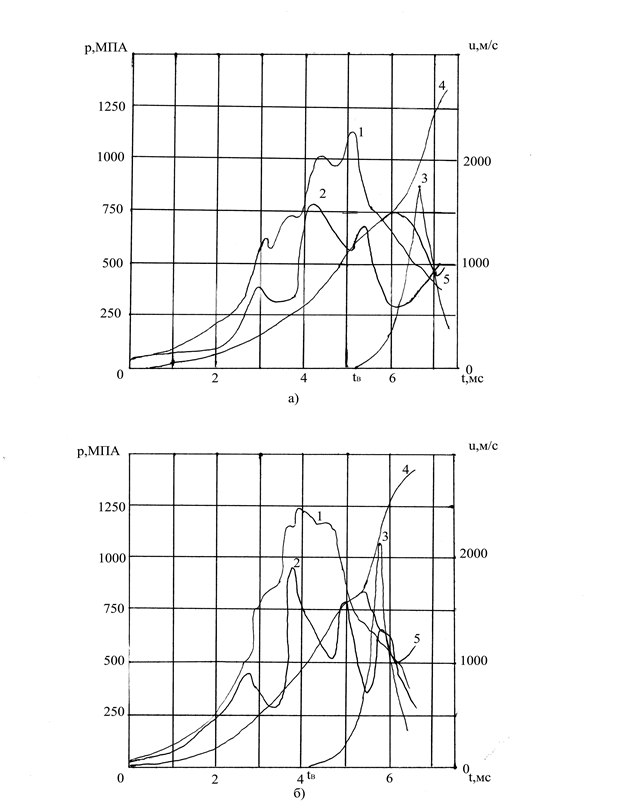
Рис. 2.2. изменение параметров в установке СПК среднего калибра в процессе выстрела: 1 - p0(t), 2 - p1(t), 3 - p2(t), 4 - Uд(t), 5 – U1(t) ;а – с неоптимальными параметрами , б- с оптимальными параметрами

В процессе оптимизации в первом приближении с коэффициентом штрафа K_i =5 получены параметры системы калибра 125 мм: V_Д = 2938 м/с, maxp₀ = 1000МПа, maxp₃ = 1250МПа. В дальнейших расчётах K_i увеличили до 69, что позволило более точно учесть ограничения (2.6).

На заключительной стадии поиска оптимальных параметров масса основного заряда увеличилась на 3,1кг, масса поршня контейнера уменьшилась на 2,7 кг. Оптимальные параметры представлены вектором х^* в таблице. При этом реализована расчётная скорость снаряда V_Д = 2830 м/с. Баллистические параметры оптимальной точки приведены на рис. 4.2,б.

Для сравнения с классической схемой выстрела был просчитан вариант с одинаковым по массе зарядом, что и при СПК, и подобрано одинаковое максимальное давление на дно канала ствола. Расчётная скорость снаряда при этом составила V_Д = 2358 м/с.

Таким образом, выигрыш в скорости при СПК по сравнению с классической схемой достигает 20%.

Определены параметры пороховой установки среднего калибра СПК, позволяющей метать снаряды с высокими скоростями в диапазоне сверхартиллерийских скоростей, при этом выигрыш в скорости по сравнению с классической схемой с теми же зарядом, массой снаряда и максимальным давлением на дно канала составляет 20%.

Заключение

1. Разработана математическая модель с использованием допущений гетерогенной среды для системы с присоединенной камерой подгона;

2. Определены оптимальные параметры СПК с использованием модели гетерогенной среды;

3. Выбран метод циклического покоординатного спуска для оптимизации рассматриваемой системы;

4. Для учета нелинейных ограничений использован метод штрафных функций;

5. Для учета линейных ограничений использован метод проектирования значения параметра на нарушенное ограничение.

6. В результате оптимизации достигнуто расчетное увеличение в скорости на 20% при неизменных максимальных давлениях на дно канала для системы калибра 125 мм.