2.2. Метод циклического покоординатного спуска

Рассмотрим метод решения максимизации функции нескольких переменных f, не использующий вычисление производных [19]. Описанный здесь метод заключается в следующем. При заданном векторе определяется допустимое направление . Затем, отправляясь из точки , функция f минимизируется вдоль направления методом циклического покоординатного спуска [20].

Задача линейного поиска заключается в минимизации f ( +  ) при условии, что L, где L обычно задается в форме L=E₁, L = {:   0} или L = {: а    b}. В формулировке алгоритма для простоты будем предполагать, что точка минимума  существует. Однако в реальных задачах это предположение может не выполняться. Оптимальное значение целевой функции в задаче линейного поиска может быть неограниченным или оптимальное значение функции конечное, но не достигается ни при каком . В первом случае целевая функция исходной задачи неограниченна и вычисления прекращаются. Во втором случае можно выбрать такое , что f( +  ) будет достаточно близким к inf{ f ( +  ): L }.

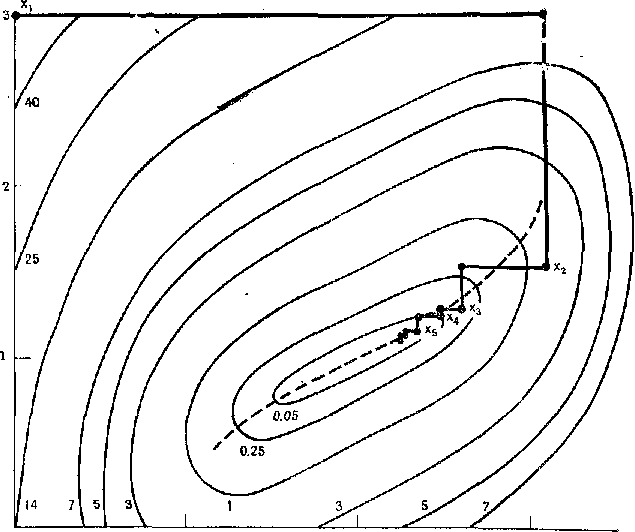
В этом методе в качестве направлений поиска используются координатные векторы. Точнее, метод осуществляет поиск вдоль направлений d₁, ..., d_n, где d_j — вектор, все компоненты которого, за исключением j-й, равны нулю. Таким образом, при поиске по направлению d_j меняется только переменная х_j, в то время как все остальные переменные остаются зафиксированными. Схематически этот метод проиллюстрирован на рис. 2.1.

2.3. Алгоритм циклического покоординатного спуска

Рассмотрим алгоритм метода циклического покоординатного спуска для минимизации функции нескольких переменных, не требующий использования производных [21].

Для остановки алгоритма могут быть использованы несколько критериев. В приведенном ниже алгоритме процесс останавливается, если . Ясно, что можно применить и любой другой критерий остановки.

Начальный этап. Выбрать число  > 0, которое будет использоваться для остановки алгоритма, и взять в качестве d₁, ..., d_n координатные направления. Выбрать начальную точку х₁, положить y₁ = х₁, k=j=1 и перейти к основному этапу.

Основной этап. Шаг 1, Положить _j равным оптимальному решению задачи минимизации f(y_j+d_j) при условии E₁.

Рис. 2.1. Тестирование метода циклического покоординатного спуска на задаче пункта. по минимизации функции (х1 — 2)4 + (х1 — 2х2)2.

Положить у_j+1=у_j +_jd_j. Если j < п, то заменить j на j+1и вернуться к шагу 1. Если j = n, то перейти к шагу 2.

Шаг 2. Положить х_k+1= у_n+1. Если || х_k+1 — х_k ||<  то остановиться. В противном случае положить у₁ = х_k+1, j=1, заменить k на k+1 и перейти к шагу 1.

Тестирование метода циклического покоординатного спуска

Рассмотрим следующую задачу: минимизировать (х₁ — 2)⁴ + (х₁ — х₂)².

Заметим, что оптимальным решением этой задачи является точка (2, 1), в которой значение функции равно нулю. В табл. 2.1. приведены результаты вычислений по методу циклического покоординатного спуска для начальной точки (0, 3). Заметим, что на каждой итерации векторы у₂ и у₃ получены посредством одномерной минимизации по направлениям (1, 0) и (0, 1) соответственно. Заметим также, что заметное убывание функции получено в течение первых нескольких итераций, тогда как на последних итерациях процесс явно замедляется. После семи итераций получена точка (2,13;1,059),

k	xk f(xk)	j	dj	yj	j	yj+1
1	(0,00, 3,00) 52,00	1 2	(1,00, 0,00) (0,00, 1,00)	(0,00, 3,00) (3,13, 3,00)	3,13 -1,50	(3,13, 3,00) (3,13, 1,50)
2	(3,13, 1,50) 1,644	1 2	(1,00, 0,00) (0,00, 1,00)	(3,13, 1,50) (2,57, 1,50)	-0,56 -0,25	(2,57, 1,50) (2,57, 1,25)
3	(2,57, 1,25) 0,107	1 2	(1,00, 0,00) (0,00, 1,00)	(2,57, 1,25) (2,32, 1,25)	-0,25 -0,13	(2,32, 1,25) (2,32, 1,12)
4	(2,32, 1,12) 0,0147	1 2	(1,00, 0,00) (0,00, 1,00)	(2,32, 1,12) (2,19, 1,12)	-0,13 -0,03	(2,19, 1,12) (2,19, 1,09)
5	(2,19, 1,09) 0,0014	1 2	(1,00, 0,00) (0,00, 1,00)	(2,19, 1,09) (2,16, 1,09)	-0,03 -0,02	(2,16, 1,09) (2,16, 1,07)
6	(2,16, 1,07) 0,0007	1 2	(1,00, 0,00) (0,00, 1,00)	(2,16, 1,07) (2,14, 1,07)	-0,02 -0,003	(2,14, 1,07) (2,14, 1,067)
7	(2,14, 1,067) 0,00047	1 2	(1,00, 0,00) (0,00, 1,00)	(2,14, 1,067) (2,13, 1,067)	-0,01 -0,008	(2,13, 1,067) (2,13, 1,059)
Таблица 2.1. Результаты вычислений по методу циклического покоординатного спуска

значение функции в которой равно f = 0,0004296.

На рис. 2.1. показаны лишь линии уровня целевой функции, точки и линии поиска, полученные методом циклического покоординатного спуска. Замедление на последних итерациях объясняется тем, что вдоль оврага, показанного пунктирной линией, делаются очень маленькие шаги по ортогональным направлениям.