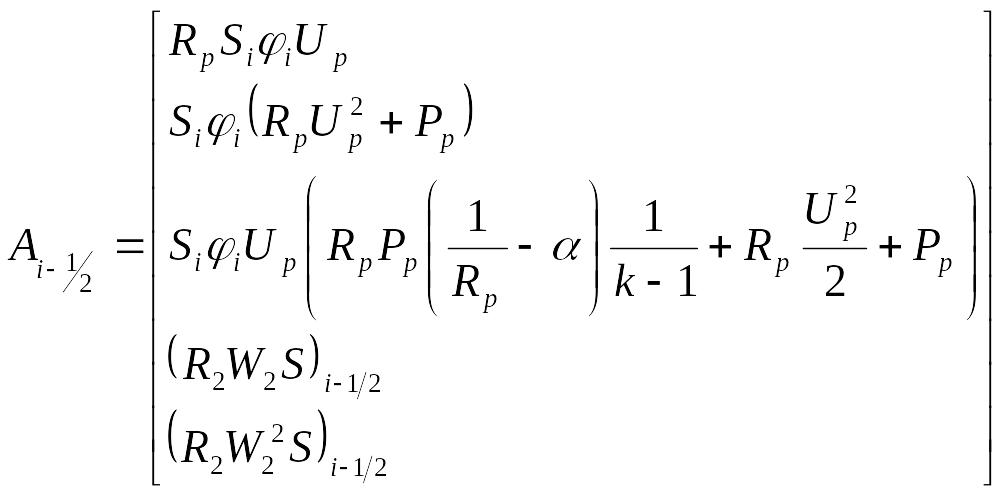1.4. Метод решения прямой задачи внутренней баллистики
Разностные формулы для уравнений (1.14) – (1.18) записываются в виде:
|
|
(1.26) |
где
|
|
(1.27) |
;
где
τ – величина шага по времени;
Fi - столбец правых частей уравнений (1.14) – (1.18)
РL, Рр, UL, Up, RL, Rp – параметры газа справа и слева на скачке сечения после распада произвольного разрыва параметров газа на скачке сечения;
R2, W2 – параметры к – фазы после распада произвольного разрыва для среды частиц.
Глава 2. Оптимизация параметров баллистической системы с камерой подгона
2.1. Постановка задачи определения оптимальных параметров в системах спк с максимальной начальной скоростью метаемого элемента
Ряд задач оптимизации в газовой динамике решается методами теории динамического программирования [4, 5, 13], оптимального управления, вариационного исчисления и т.д. Однако аналитическое решение задач на основе упомянутых методов возможно лишь в относительно простых случаях, которые далеки от потребностей практики. В общих случаях применяют приближенные численные методы, среди которых методы нелинейного программирования [14, 15], то есть методы определения экстремума функции многих переменных при выполнении ряда ограничений наиболее универсальны.
В нашем случае объектом оптимизации являются газодинамические процессы метания тел в системах эстафетной схемы выстрела. Как правило, эти процессы зависят от многих параметров, которые меняются в определенных пределах. При этом основные показатели, такие как скорость метаемого элемента, максимальные давления на дно метаемого элемента в канале системы меняются в широких диапазонах. В этом случае возникает задача о выборе параметров наилучшим образом. Сведем нашу задачу к задаче нелинейного программирования (НЛП). При сведении вариационной задачи газовой динамики к задаче НЛП, исходный функционал приближенно заменяется на функцию многих переменных [16].
Процессы метания из установок с присоединенной камерой подгона выстрела описываются системами уравнений в частных производных, в соответствии с математической моделью, данной в 1.3. Будем считать, что нам удалось свернуть все показатели качества процесса в один обобщенный критерий оптимальности [17]. В этом случае задачу оптимизации запишем:
max F(u1, u2,…, um, ) |
(2.1) |
GJ(u1, u2,…, um, ) 0, j = 1, …, l |
(2.2) |
H() 0, = 1, …, n, |
(2.3) |
где F, GJ, H – некоторые операторы,
u1(t, x, ), u2(t, x, ),…, um(t, x, ) – решения краевых задач в соответствии с принятой математической моделью СПК.
Условия (2.2) зависят от решения краевой задачи, а (2.3) не связаны с математической моделью процесса и определяют технические требования к рассматриваемой высокоскоростной метательной системе.
Ограничения существенно меняют область поиска. Особенностью таких задач является то, что экстремум в допустимой области может не достигаться.
Будем искать оптимальное решение для систем эстафетной схемы выстрела при ограничении на максимально допустимые давления в системах. Линейные ограничения будем накладывать на массу поршня схемы с воспламенительным устройством и время или координату задержки зажигания. При нарушении линейных ограничений значения ограничений проектируются на нарушенные параметры.
Нелинейные ограничения учитываются методом штрафных функций [18]. В этом случае задача безусловной минимизации (2.1 – 2.3) преобразуется в задачу безусловного поиска для другой целевой функции:
max (Ф(, i )/ B), |
(2.4) |
Ф(,
i
) =F()
–
|
|
|
|
,
j = 0, …, 3.где i – весовой коэффициент.
Ограничения
выбираются конкретно для различных
систем в зависимости от допустимых
максимальных давлений.
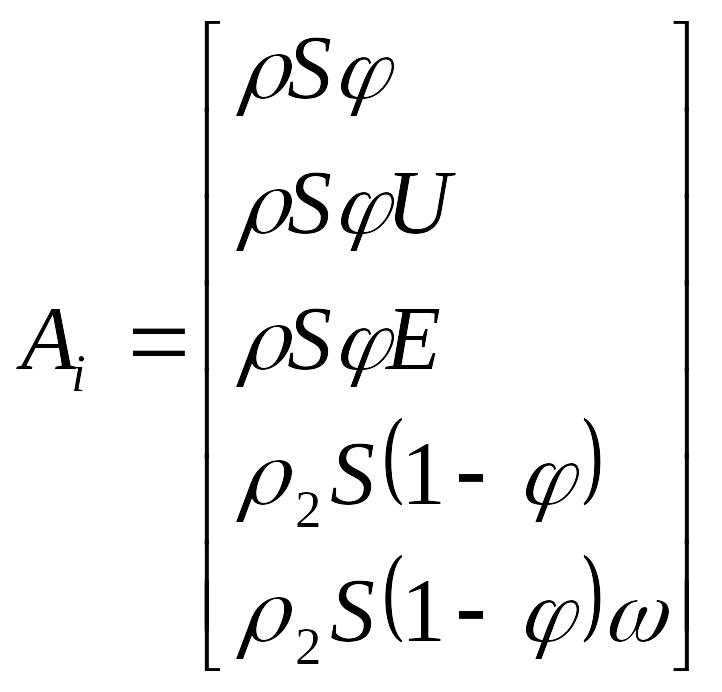
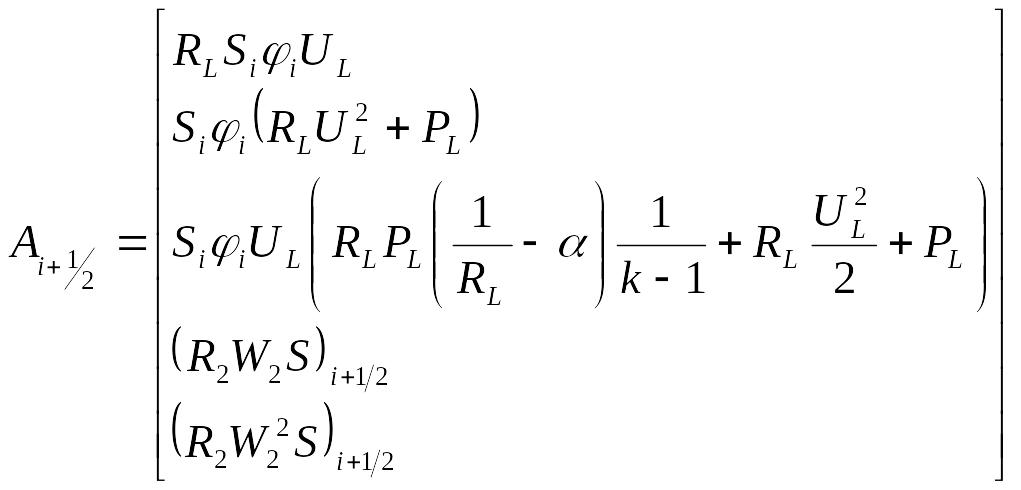