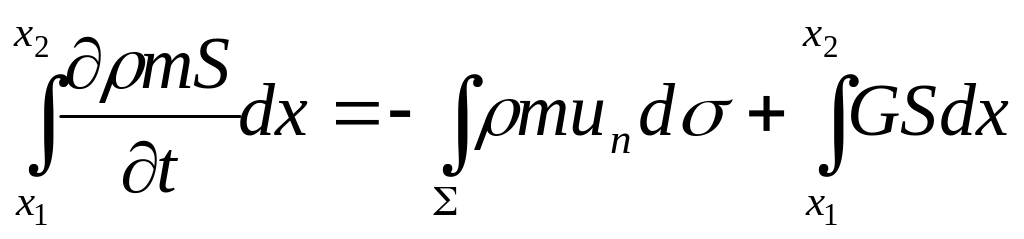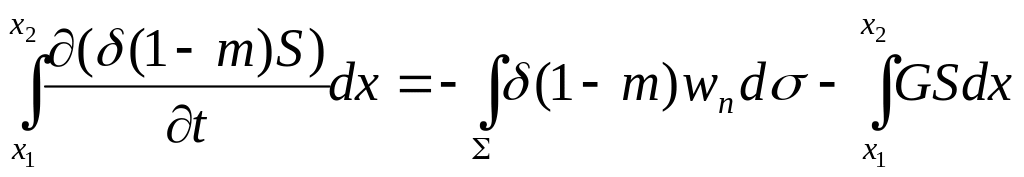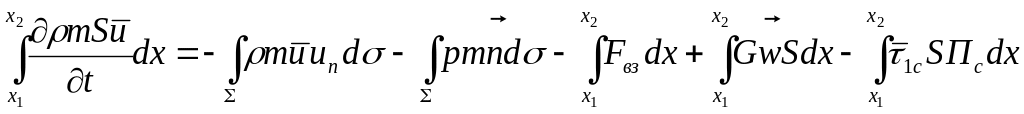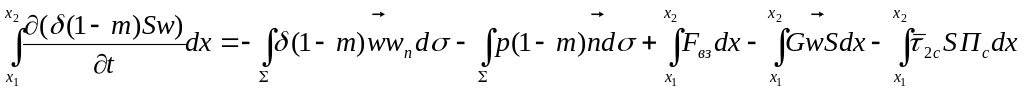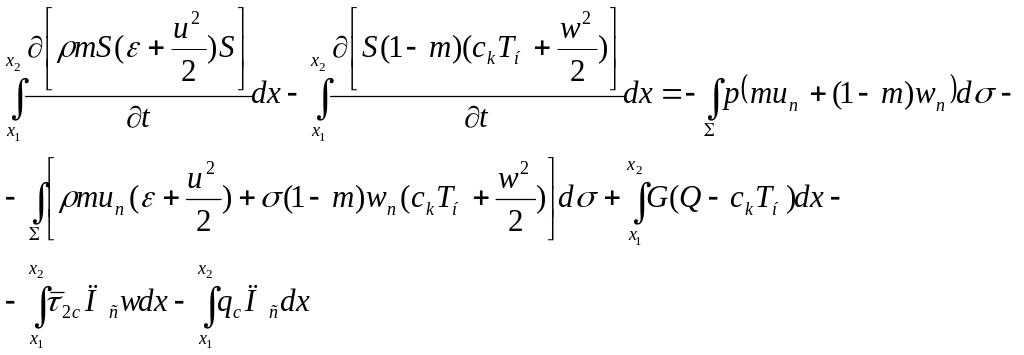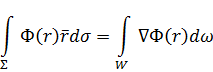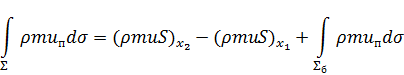1.2. Математическая постановка задачи

Будем рассматривать двухфазный поток, состоящий из пороховых газов и совокупности горящих частиц зерненного пороха, характерный размер и концентрация которых такова, что выполняется допущение.

Дополнительно примем следующие допущения, связанные со спецификой задачи:

1) движения фаз одномерно;

2) теплоотдача к горящей поверхности зерен не учитывается (скорость движения тепловой волны в порохе равна скорости горения);

3) материал частиц несжимаем;

4) параметры газа внутри и вне пороховых элементов в данном сечении одинаковы.

При выводе квазиодномерных уравнений двухфазной реагирующей смеси мы исходили из пространственной системы уравнения движения, которые не содержат члены, характеризующие взаимодействие со стенками канала ствола [11]. Поэтому дадим краткий вывод одномерных уравнений, где такое взаимодействие учитывается. В постановку задачи должны входить уравнения, полученные на основе законов сохранения массы, импульса и энергии для газа, а так же массы и количества движения для твердой фазы. В силу допущений 2), 3) уравнение энергии для твердой фазы не требуется.

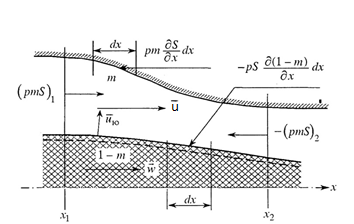
Рассмотрим одномерное течение двухфазной смеси в фиксированном объеме W, определенном координатами x₁, x₂ (рис. 1.2.) и ограниченном поверхностью Σ. Как показано выше, в однородной среде объемная пористость равна поверхностной. Данное утверждение, строго говоря, не выполняется на непроницаемых поверхностях (в нашем случае боковая поверхность канала). Тем не менее, будем считать, что гипотеза сплошной среды справедлива как угодно близко к боковой поверхности канала. Тогда, не смотря на не проницаемость стенок, можно принять, что пористость среды на стенке равна объемной пористости. Очевидно, данное предположения будет выполняться тем точнее, чем сильнее неравенство ℓ/d_кн << 1, где ℓ - характерный размер включений. Рамки гипотезы сплошной среды предполагают также, что на боковой поверхности происходит абсолютно неупругое взаимодействие твердой фазы (имеет место условие

Рис. 1.2. схематическое представление двухфазного реагирующего потока

скольжения.

С учетом этих замечаний уравнения сохранения массы для обеих фаз внутри объема W имеют вид:

		(1.1)
		(1.2)

Уравнения импульсов каждой из фаз можно представить аналогичным образом:

	(1.3)
	(1.4)

где , – векторы сил трения газа и пороховых частиц о поверхность ствола, приходящиеся на единицу площади соответственно.

В одномерном случае силу межфазного взаимодействия, приходящуюся на единичный объем гетерогенной среды, необходимо представить так:

(1.5)

где первая составляющая обусловлена разностью скоростей между фазами, вторая – давлением газа в связи с расширением или сужением трубки тока второй фазы (рис. 1.2.).

Полная энергия смеси в объеме W изменяется за счет притока энергии извне, работы сил давления на ограничивающей поверхности Σ, притока химической энергии за счет горения пороховых зерен, теплообмена с поверхностью канала и расхода механической энергии твердой фазы за счет трения «газа частиц» о поверхности ствола. Итак,

(1.6)

где q_c – тепловой поток на поверхность канала ствола.

Последний член уравнения (1.6) записан для математической корректности. Его отсутствие при постоянной внутренней энергии твердой фазы означало бы, что работа сил трения частиц о поверхность ствола способствует повышению энергии газа, тогда как единственно возможный механизм передачи энергии между фазами – это межфазовое взаимодействие. Реально тепло, связанное с этим членом, идет на нагрев материалов ствола и пороховых частиц при соударении. Этими эффектами будем пренебрегать.

Используя теорему о градиенте:

(1.7)

справедливую для непрерывных подынтегральных функций в W и на Σ, в одномерном случае получаем

(1.8)

где – единичный вектор в направлении оси x.

Для остальных поверхностных интегралов соответствующая теорема Гаусса–Остроградского неприменима, так как подынтегральные функции терпят разрыв при переходе на боковую поверхность ограничивающей поверхности Σ. Их можно расписать следующим образом, например:

(1.9)

Интеграл по боковой поверхности обращается в нуль, так как на стенке =0.

Предполагая, что внутри объема W нет разрывов, разделив обе части уравнений (1.1) – (1.4), (1.6) на (Δx = x2 – x1) и переходя к пределу при Δx → 0. Используя преобразования (1.8), (1.9), осуществляем переход от интегральной формы записи уравнений к дифференциальной.

Полученная система уравнений содержит семь неизвестных: параметры газа скорость твердой фазы w, пористость смеси m и относительную долю сгоревшего пороха

В практических расчетах для зерненых порохов удобно заменить уравнения неразрывности твердой фазы уравнением для счетной концетрации пороховых элементов :

(1.12)

тогда пористость смеси определится из выражения

(1.13)