13. Кручение тонкостенного стержня с замкнутым контуром сечения. Формулы Бредта для вычисления касательного напряжения и угла закрутки ( с пояснениями параметров, входящих в них).

, где А* - площадь просвета трубы, t – ее толщина. , где - относительный периметр (в случае постоянной толщины: , в случае разных толщин: )

14. Формулы для вычисления касательного напряжения и угла закрутки тонкостенного стержня с открытым контуром сечения.

Динамические задачи

15. Что такое коэффициент динамичности kд при ударе? Формула вычисления коэффициента динамичности kд при заданной высоте падения груза на вертикальный брус

Коэффициент динамичности: . Здесь сила, которая равна весу F ударяющего тела и действует статически, . - сила удара , - деформация стержня для задачи о статическом нагружении. При заданной скорости груза Здесь v- скорость ударяющего тела Область применимости коэффициент динамичности:

Тестовые вопросы

16. Во сколько раз увеличится нагрузка, которую может выдержать проволока, если ее радиус увеличить в 2 раза?

Ответ: в 4 раза, т.к. N=σ∙A= σ∙π∙r²

17. Во сколько раз увеличится нагрузка, которую может выдержать балка квадратичного сечения, изготовленная из хрупкого материала, если сторону квадрата увеличить в 2 раза?

Ответ: в 8 раз, т.к. σ_max=M_x/W_x, M_x =P∙l, W_x= a³/6

1 8. Во сколько раз уменьшится нагрузка, которую может выдержать балка, если длину увеличить в 2 раза?

Ответ: в 2 раза, т.к. σ_max=M_x/W_x, M_x =P∙l,

19. Во сколько раз увеличится сжимающая критическая нагрузка, которую может выдержать длинная упругая балка квадратного сечения, если сторону квадрата увеличить в 2 раза ?

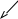
Ответ: в 16 раза, т.к. Р_кр=∙π²∙J_x/E(μ∙l)², J_x = a⁴/12

20. Как различаются нагрузки, которые могут выдержать балки прямоугольного сечения, изготовленная из хрупкого материала, (b:h=1:2), если первая изгибается в плоскости меньшей жесткости, а вторая - в плоскости большей жесткости?

.

Ответ: в 2 раза, т.к. σ_max=M_x/W_x, M_x =P∙l,

В первом случае W_x= bh²/6= 2a³/6, во втором случае W_x= bh²/6= 4a³/6,

21. Как различаются прогибы балок прямоугольного сечения (b:h=1:2) , если первая изгибается в плоскости меньшей жесткости, а вторая - в плоскости большей жесткости?

Ответ: в 4 раза, т.к. v= ∫∫ M_x/EJ_x dz

В первом случае J_x= bh³/12= 2a³/12, во втором случае J_x= 4bh²/12= 8a³/12,

22. В сколько раз увеличится предельный момент, который может выдержать труба при кручении, если ее радиус увеличить в 2 раза, а толщину оставить прежней

Ответ: в 4 раза, т.к. τ = M_z/2At_o , A=∙π∙r²