Оптимальные сроки эксплуатации

Отказы систем, находящихся на хранении, либо не используемых достаточно долгое время, а также резервированных систем, не снабженных средствами сигнализации о возникновении неисправности, выявляются при проведении профилактических работ.

Покажем, что вероятность нахождения системы в состоянии готовности к использованию по назначению зависит от периодичности профилактических работ.

После отказа до очередной профилактической работы (очередного технического обслуживания) в продолжение времени t^▪_пр система находится в неработоспособном состоянии. Весь межпрофилактический интервал t_п состоит из времени работоспособного t^▪_р и неработоспособного t^▪_пр состояний, то есть t_п=t^▪_пр+ t^▪_р. Кроме того, на протяжении времени выполнения профилактических работ t^▪_прф система, разумеется, не используется по назначению (рис.7.3).

t_прф t^▪_p t^▪_пр t^▪_прф

рис. 7.3 периодичность и время проведения профилактических работ

Таким образом, доля времени, в течение которого можно, с технической точки зрения, использовать систему по назначению, определяется выражением:

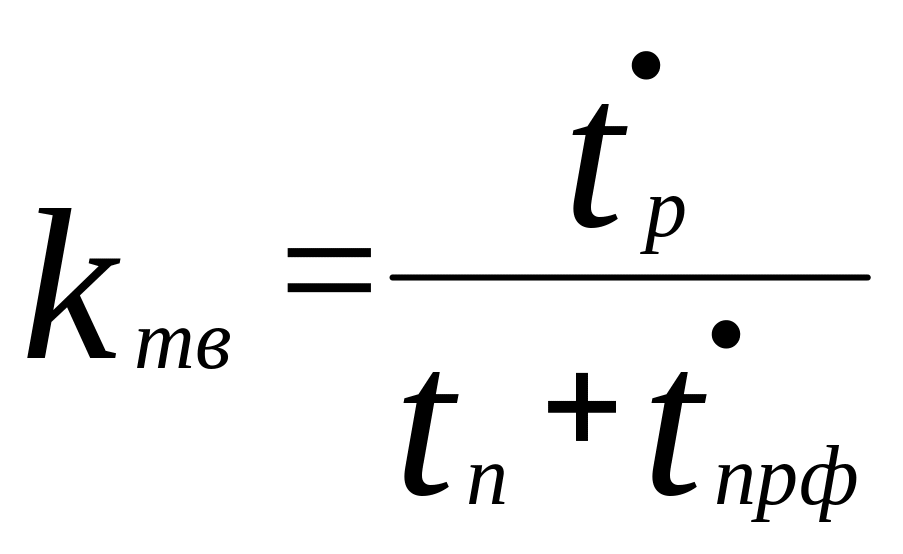(7.1)

Время работоспособного состояния системы при показательном законе распределения его вероятностей

(7.2)

Тогда

(7.3)

Оптимальная периодичность профилактических работ соответствует К_ТВ=К_ТВмакс; ее можно определить и графически (рис. 7.4).

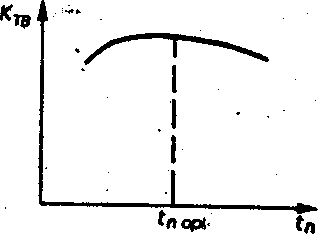
рис. 7.4 определение оптимальной периодичности профилактических работ

Аналитическое решение (взять производную по t_n и приравнять её к нулю) дает (при стандартных допущениях) следующий результат:

. (7.4)

Периодичность профилактических работ может быть скорректирована по данным эксплуатации. При этом по статистическим данным определяется оценка λ* интенсивности отказов и задаются требования к уровню надежности в виде вероятности нахождения системы в технически исправном состоянии р_треб. Вероятность того, что в межпрофилактическом интервале t_n система исправна, приравнивается к Р_лре6, тогда

(7.5)

Прологарифмировав (7.5), получаем значение времени до следующих профилактических работ:

. (7.6)

Таким образом, при заданной величине р_треб периодичность обслуживания с целью восстановления работоспособного состояния определяется интенсивностью отказов элементов.

Экпоненциальная оценка надежности Оценка параметров закона распределения

Наиболее полной характеристикой надежности объекта является функция распределения вероятностей времени безотказной работы, то есть закон распределения. В настоящее время в результате многочисленных экспериментальных и теоретических исследований области применения большинства законов распределения, в основном, известны. Поэтому мы не будем, ввиду большой сложности материала, рассматривать строгие методы определения законов распределения. В этом нет необходимости еще и потому, что о виде распределения можно судить по эмпирической функции распределения и гистограмме (см. п. 6.2).

Например, известно, что в период нормальной эксплуатации закон распределения вероятностей времени безотказной работы показательный с λ = const.

Таким образом, неизвестной величиной является только значение λ, которое требуется определить по результатам эксплуатации.

Для оценки неизвестных параметров законов распределения разработано несколько методов, но наиболее широко и эффективно используется метод наибольшего правдоподобия, предложенный английским статистиком Р. Фишером в 1912 году. Рассмотрим его применение для определения интенсивности отказов λ.

Допустим, что в процессе эксплуатации находилось n одинаковых объектов (систем, подсистем, агрегатов, элементов). Наработка каждого объекта до его отказа имеет значение:

t₁, t₂, …., t_n, . (7.7)

Вероятность каждого из этих значений в малом интервале времени (t_i + ∆t) равняется f(t_i)∆t_i, где f(t_i)-дифференциальная функция распределения вероятности (плотность вероятности) наработки i-гo объекта до отказа.

При условии независимости отказов вероятность совместного появления всех значений (7.7) равняется произведению вероятностей, то есть

P=f(t₁), f(t₂)…f(t_n)∆t₁∆t₂…∆t_n. (7.8)

Наиболее вероятным будет такое значение интенсивности отказов λ, при котором максимально значение вероятности р. Рассмотрим вспомогательную функцию

(7.9)

которая достигает максимума при том же значении λ, что и вероятность р. При показательном законе распределения вероятности наработки до отказа плотность вероятности

f(t)=λe^-λt (7.10)

Тогда

(7.11)

Для определения интенсивности отказов λ надо взять частную производную выражения (7.11) по λ и приравнять ее к нулю:

(7.12)

(Если воспользоваться данными примера, приведенного в п. 6.2, то применение формулы (7.12) даст результат: λ^* = 30/17015 = 7,6 • 10^-3/ч;.).

Аналогично определяются параметры закона нормального распределения вероятностей наработки до отказа (при износовых отказах, третий этап эксплуатации):

(7.13)