
- •2. Для расчёта оценки среднеквадратического отклонения погрешности результата наблюдений (стандартной неопределенности единичного измерения) s необходима формула: 2.13 на странице 42 учебника [2].
- •3. Максимальная погрешность результата наблюдений макс или предельно допустимая погрешность определяется по формуле:
- •4 Для определения систематической погрешности воспользуемся формулой:
- •5 Границы суммарной погрешности поверяемого вольтметра определяют путем алгебраического сложения систематической погрешности с максимальной случайной погрешностью
- •6 Предел допускаемой погрешности исследуемого вольтметра находят по его классу точности, указанному в условиях задачи
- •7 Оценку среднеквадратического отклонения результата измерения s(u) рассчитаем по формуле:
- •8 Доверительный интервал - интервал, в который попадает результат измерения с заданной вероятностью р. Этот интервал рассматривается как допустимое значение погрешности измерения величины.
- •9 Результат измерения
- •1 Рабочее ослабление Ар исследуемого четырехполюсника.
- •2 . Рабочее ослабление измеряют, используя выражение 2.4.
- •7 Результаты измерений
- •1. Метрология, стандартизация и измерения в технике связи/ Под ред. Б. П. Хромого. - м.: Радио и связь, 1986. -418с.
- •2. Кушнир ф. В., Савенко в. Г., Верник с. М. Измерения в технике связи. - м.: Связь, 1976. - 432 с.
- •3 Запасный и. Н., Сметанин в. И. Метрология, стандартизация и сертификация. Контрольное задание и методические указания. - н.: 2004. - 36 с.
Вариант 27
Задача 1
При поверке вольтметра Vn
с помощью образцового
вольтметра Vo (см.
рисунок 1.1) был получен ряд из /I результатов
наблюдений (единичных измерений)
напряжения Uo образцовым
вольтметром путем многократной
установки на поверяемом вольтметре Vn
одного и того же
показания- Класс точности поверяемого
вольтметра у. Считая,
что случайная составляющая погрешности
исследуемого вольтметра распределена
по нормальному закону, а погрешность
образцового вольтметра пренебрежимо
мала, найти следующие величины.
1. Действительное значение измеряемого
напряжения (результат измерения
при многократных наблюдениях)
U.
2. Оценку среднеквадратического
отклонения (СКО) случайной составляющей
погрешности поверяемого вольтметра
(оценку СКО результата наблюдений
(стандартную неопределенность единичного
измерения)) S.
3. Границу максимальной
погрешности случайной составляющей
погрешности исследуемого вольтметра
(максимальную погрешность результата
наблюдений) Амакс.
4. Систематическую составляющую
погрешности поверяемого вольтметра.
5. Границы суммарной (случайной и
систематической) погрешности поверяемого
вольтметра.
6. Предел допускаемой
погрешности исследуемого вольтметра.
Построить график его зависимости от
показаний вольтметра Uy-
Показать на графике
найденные границы суммарной погрешности
вольтметра и сделать вывод о пригодности
средства измерения к применению.
7. Оценку среднеквадратического
отклонения случайной составляющей
погрешности исследуемого вольтметра
при n-кратных
наблюдениях (оценку СКО результата
измерения (стандартную неопределенность
результата измерения)) s(v).
8. Границы доверительного
интервала случайной составляющей
погрешности(расширенную неопределенность)
Е для
результата измерения при n-кратных
наблюдениях напряжения исследуемым
вольтметром при заданной доверительной
вероятности Р.
9. Записать в соответствии с нормативными
документами результат измерения
напряжения поверяемым вольтметром при
и-кратных наблюдениях, исключив из
показания вольтметра t/я систематическую
составляющую погрешности.
10. Предложить способ уменьшения оценки
СКО случайной
составляющей погрешности
результата измерения поверяемым
вольтметром в D раз
по сравнению с единичным измерением
(оценкой СКО результата наблюдений).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
в соответствие с таблицами 1,1 1,2 и 1,3
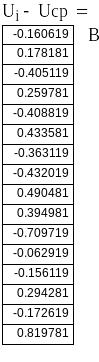
1. Истинное значение U измеренной величины
неизвестно, поэтому при числе измерений
равное n вместо значения U берут наиболее
достоверное значение -среднее
арифметическое, которое вычисляется
по формуле:
[1.С.67, ф.(4.6)]
Для данного случая формула будет
выглядеть так:
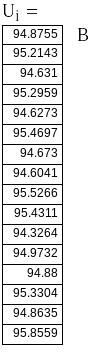
где n- число наблюдений, i -
номер измерения, Uх - результат единичного
измерения. После подстановки числовых
значений получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
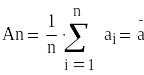
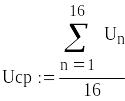
![]()
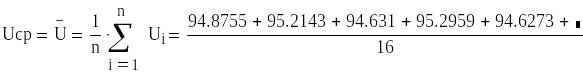
![]()
![]()
![]()
![]()
где vi - отклонение результата единичного
измерения а, от среднего значения Acp,
n- число наблюдений
Вычислим погрешность округления:
Погрешность округления не превышает
5%, следовательно, округление верное.

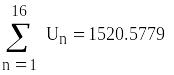
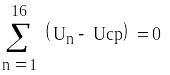
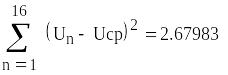
![]()
2. Для расчёта оценки среднеквадратического отклонения погрешности результата наблюдений (стандартной неопределенности единичного измерения) s необходима формула: 2.13 на странице 42 учебника [2].
![]()
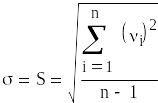
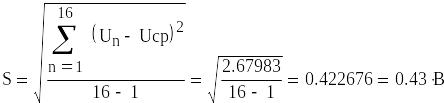
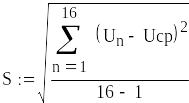
![]()
![]()
![]()
![]()
где S среднеквадратическое
отклонение погрешности результата
наблюдения.
[2.С.43]
Вычислим погрешность округления:
Погрешность округления не превышает
5%, следовательно, округление верное.
[З.С.20]
действительное значение
результат измерения
Погрешность округления не превышает
5%, следовательно, округление верное.
Погрешность округления не превышает
5%, следовательно, округление верное.
3. Максимальная погрешность результата наблюдений макс или предельно допустимая погрешность определяется по формуле:
![]()
![]()
![]()
![]()
4 Для определения систематической погрешности воспользуемся формулой:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5 Границы суммарной погрешности поверяемого вольтметра определяют путем алгебраического сложения систематической погрешности с максимальной случайной погрешностью
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
класс точности
An предел измерения
Так
граница суммарной погрешности поверяемого
вольтметра превышает предел
допускаемой погрешности
вольтметр не соответствует классу
точности
[2.С.43,ф.(2.14)]
где Sa- приближенное значение
среднеквадратической погрешности sа
ряда из n наблюдений.
6 Предел допускаемой погрешности исследуемого вольтметра находят по его классу точности, указанному в условиях задачи
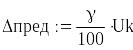
![]()
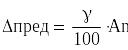
![]()
![]()
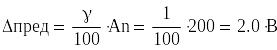

![]()
![]()
![]()
7 Оценку среднеквадратического отклонения результата измерения s(u) рассчитаем по формуле:
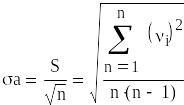
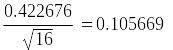
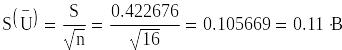
Для расчета доверительного интервала
необходима формула:
По таблице приложения II [1] определим
коэффициент Стьюдента для n=16 и
Доверительный интервал
[3.C.20]
±
условия измерения нормальные
10 При выполнении задания считаем, что
результаты наблюдений распределены
по нормальному закону. Точечная оценка
дисперсии для результата наблюдений
(квадрат СКО результата наблюдений)
необходимо изменить n. Отсюда можно
получить новое число наблюдений, которое
позволит уменьшить
в заданное число D раз.
Из этих рассуждений можно получить
формулу для вычисления числа наблюдений,
необходимого для уменьшения
в
заданное число D раз:
раз необходимо увеличить количество
измерений
Для уменьшения оценки СКО в
8 Доверительный интервал - интервал, в который попадает результат измерения с заданной вероятностью р. Этот интервал рассматривается как допустимое значение погрешности измерения величины.
![]()
![]()
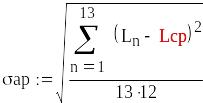
![]()
![]()
![]()
9 Результат измерения
![]()
![]()
![]()
![]()
![]()
![]()
![]() при большом числе наблюдений (в пределе
при n к )
стремится к постоянной величине
-дисперсии результата наблюдений
при большом числе наблюдений (в пределе
при n к )
стремится к постоянной величине
-дисперсии результата наблюдений
![]() [1.C.73]. Известно [1.С.74, ф. (4,24)], что оценка
СКО результата измерений зависит от
СКО результата наблюдений и числа
наблюдений
[1.C.73]. Известно [1.С.74, ф. (4,24)], что оценка
СКО результата измерений зависит от
СКО результата наблюдений и числа
наблюдений
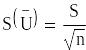 Из этого выражения видно, что для
изменения
Из этого выражения видно, что для
изменения
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
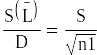
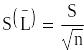
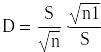
![]()
![]()
![]()
Задача 2
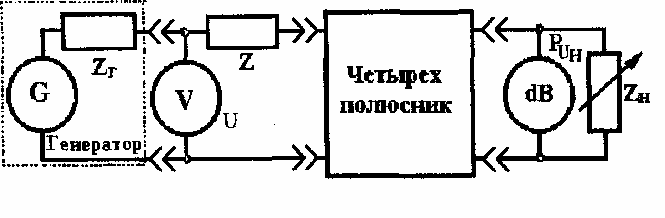
Рабочее ослабление Ар
четырехполюсника
измерено методом Z на частоте 1000Гц
(рисунок 2.1). Четырехполюсник нагружен
со стороны входных зажимов на сопротивление
Z, а со стороны выходных зажимов на
сопротивление ZH. Напряжение на выходе
генератора U и
абсолютный уровень напряжения на выходе
четырехполюсника рцн
измеряли милливольтметром
ВЗ-38 класса точности у с высокоомным
входным сопротивлением.
В зависимости от варианта, определяемого
последними двумя цифрами М и N номера
зачетной книжки, в соответствии с
исходными данными, указанными в таблицах
2.1 и 2.2, необходимо определить.
1. Рабочее ослабление Ар
исследуемого
четырехполюсника.
2. Оценку границ абсолютной погрешности
измерения рабочего ослабления
3. Записать результат
измерения Ар в
соответствии с нормативными документами.
сопротивление нагрузки четырехполюсника
со стороны входных зажимов;
напряжение на выходе генератора,
измеренное милливольтметром ВЗ-38
сопротивление нагрузки четырехполюсника
со стороны выходных зажимов
абсолютный уровень напряжения, измеренный
милливольтметром ВЗ-38 на нагрузочном
сопротивлении Zn
c/d=1.5/0.5%
две составляющие С
и d
условного обозначения
класса точности сопротивления;
конечное значение диапазона
измерений магазина сопротивления Zn.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
