Часть электрической цепи, имеющая две пары зажимов для присоединения к остальной части цепи, называется четырехполюсником и изображается на схеме, как показано на рис. 9.1. Зажимы, принадлежащие одной паре, называются входными и обычно служат для присоединения к источнику энергии (1, 1¢). Два других, к которым обычно подключается нагрузка, называются выходными (2, 2¢). Примеры: трансформатор, двухпроводная линия электропередачи, мостовая схема. На практике возможны и иные варианты подключения четырехполюсника.

Реальная схема соединений элементов, составляющих четырехполюсник, и их параметры могут быть и неизвестны. В этом случае пользуются некоторыми обобщенными величинами, достаточными для составления уравнений, связывающих напряжения и токи на зажимах четырехполюсника.

Если параметры четырехполюсника не зависят от режима работы, он называется линейным, в противном случае – нелинейным.

Если он не содержит источников электрической энергии, то именуется пассивным (П, рис. 9.2), если содержит, то активным (А, рис. 9.1).

Активные четырехполюсники в свою очередь делятся на автономные и неавтономные. У автономных существует напряжение хотя бы на одной паре зажимов даже при отключении четырехполюсника от остальной части цепи. У неавтономных в этом случае напряжение на разомкнутых зажимах отсутствует. Их внутренние источники являются зависимыми (пример – триод).

Если четырехполюсник удовлетворяет принципу взаимности, он называется обратимым, в противном случае – необратимым. Отметим, что пассивные линейные четырехполюсники всегда обратимы.

Если при перемене мест подключения входных и выходных зажимов четырехполюсника его режим работы не меняется, то такой четырехполюсник называется симметричным, в противном случае – несимметричным. В этом разделе (за исключением одного параграфа) рассматриваются линейные пассивные четырехполюсники в установившемся синусоидальном режиме. Поэтому все соотношения удобно записывать в комплексной форме.

9.2. Основные уравнения четырехполюсника

Эти уравнения связывают напряжения и токи на входе и выходе четырехполюсника. Возможны шесть вариантов записи основных уравнений. При этом следует обратить внимание на возможные различные направления токов в схеме рис. 9.2: .

Уравнения в форме :

или в матричной записи ,

где

Здесь и – входные проводимости четырехполюсника относительно первичных и вторичных зажимов, и – взаимные проводимости. При коротком замыкании выходных зажимов можно определить ; . При обратном коротком замыкании и тех же направлениях токов можно найти и 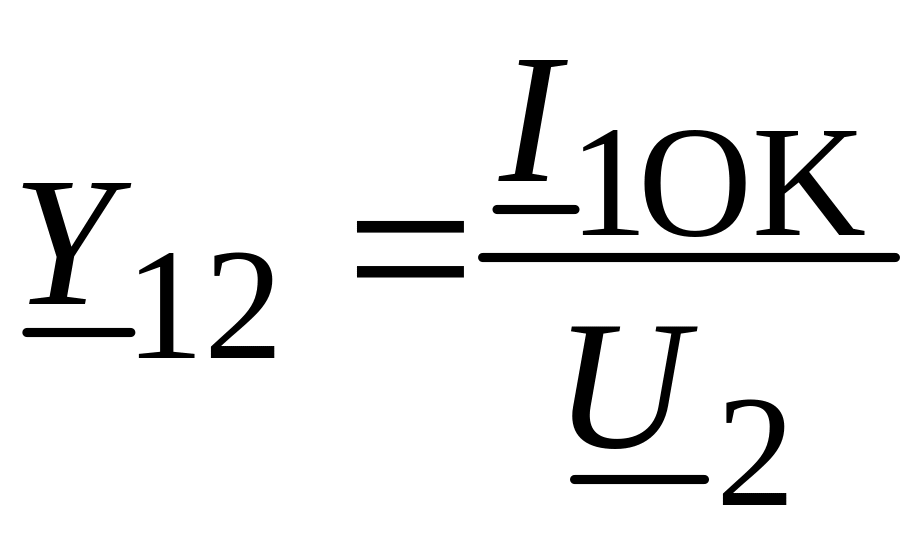. Из принципа взаимности следует .

Уравнения в форме :

или , где ,

а U и I – те же матрицы-столбцы, что и в предыдущем случае.

Здесь и – входные сопротивления четырехполюсника относительно первичных и вторичных зажимов, и – взаимные сопротивления. В режиме прямого холостого хода можно определить ; .

При подключении источника с напряжением к выходным зажимам и размыкании входных (обратный холостой ход – ) можно найти

; .

Выполняется принцип взаимности: = .

Очевидно, , то есть взаимно обратны матрицы, а не их компоненты. Легко заметить, что матричные уравнения и имеют вид закона Ома.

Уравнения в форме :

или , где .

Здесь коэффициенты и безразмерны, имеет размерность сопротивления, – проводимости. При прямом включении в режиме холостого хода определяются

; .

А в режиме короткого замыкания можно найти

; .

Сравним последние формулы с описанием того же режима в форме . Тогда, учитывая, что , найдем

; .

Продолжив сравнение в режиме холостого хода, обнаружим, что

; .

Нетрудно убедиться, что

Способ более простого экспериментального определения коэффициентов четырехполюсника в форме рассматривается ниже.

Уравнения в форме :

или , где .

Как и в предыдущей паре формул, коэффициенты и безразмерны, имеет размерность сопротивления, – проводимости. В режиме обратного холостого хода легко определяются ; , а в режиме обратного короткого замыкания находятся ; (оба режима с изменением направления токов). Если уравнения в форме разрешить относительно и , то получим:

Но перемена направлений токов ( , ) должна привести к форме . Следовательно,

= ; = ; = , = .

Еще две формы записи уравнений связывают , с , и , с , . Они употребляются реже.

Форма : или .

Форма : или .

Разнообразие форм записей уравнений четырехполюсников обусловлено удобством использования той или иной формы при различных схемах их соединений. Но при любой форме из четырех коэффициентов четырехполюсников независимы только три.

9.3. Схемы соединения четырехполюсников

Рассмотрим наиболее часто встречающиеся схемы соединения четырехполюсников на примере двух четырехполюсников, матрицы ко-

эффициентов которых известны, и заменим их одним эквивалентным, связав его коэффициенты с соответствующими коэффициентами исходных четырехполюсников. Последовательное соединение четырехполюсников – такое их соединение, при котором по входным зажимам обоих четырехполюсников течет один и тот же ток и по выходным зажимам – один и тот же ток (рис. 9.3). В этом случае ; .

Тогда в матричной форме .

Следовательно,

Параллельное соединение четырехполюсников – такое их соединение, при котором входные зажимы обоих четырехполюсников подключены к одному напряжению и выходные зажимы обоих четырехполюсников подключены к одному напряжению (рис. 9.4).

Очевидно, ; ,поэтому в матричной форме .

Следовательно,

Каскадное соединение четырехполюсников – такое их соединение, при котором входные зажимы одного четырехполюсника (последующего) подключены к выходным другого (предыдущего) – рис. 9.5.

При этом , но

тогда

Для определения параметров эквивалентного четырехполюсника при параллельно-последовательном или последовательно-параллельном соединениях двух четырехполюсников используются соответственно формы записи основных уравнений и .