8. Трехфазные цепи

8.1. Основные понятия и определения

В 1891 году русский инженер-электротехник Михаил Осипович Доливо-Добровольский доказал эффективность трехфазных систем, разработав и построив все необходимые компоненты трехфазной цепи (генератор, асинхронный двигатель, трансформатор, линию электропередачи). С тех пор эти цепи исправно служат человеку.

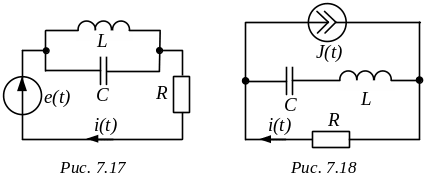
Трехфазной системой ЭДС называется совокупность трех синусоидальных ЭДС одинаковой частоты, сдвинутых относительно друг друга по фазе и создаваемых общим источником электрической энергии. Принцип получения такой системы ЭДС иллюстрирует рис. 7.1. Отличие от принципиальной схемы получения одной синусоидальной ЭДС (см. раздел 4.1) заключается лишь в использовании трех одинаковых рамок вместо одной.

Эти рамки, каждая с числом витков w , закрепленные на общей оси, вращаются с постоянной угловой скоростью  в равномерном магнитном поле постоянного магнита. Их плоскости составляют друг с другом угол 60. Одна тройка одноименных зажимов (начала) этих обмоток обозначена буквами A, B, C, другая (концы) – a, b, c. Каждую из обмоток, как показано в разделе 4.1, пронизывает гармонический магнитный поток. Очевидно, при вращении рамка Bb повторяет путь рамки Aa с запаздыванием в одну треть периода, а рамка Cc – с запаздыванием в две трети периода.

Если считать, что положение рамок на рис. 7.1 соответствует моменту времени t = 0, то магнитный поток, пронизывающий каждую из рамок, изменяется по закону: ; ; .

В свою очередь ЭДС, возникающие в обмотках, изменяются по синусоидальному закону:

, где ; аналогично

; .

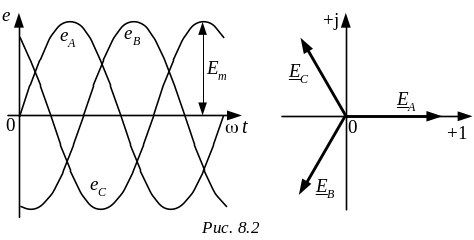
Волновая и векторная диаграммы этой системы ЭДС показаны на рис. 8.2.

Для сокращения записи комплексных изображений трехфазных систем в расчет вводится так называемый фазовый оператор 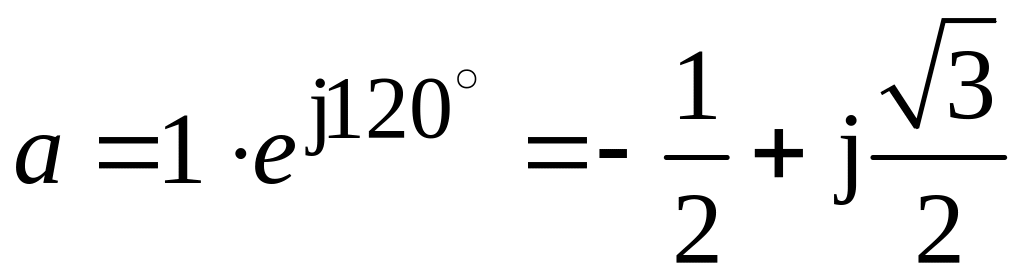, умножение и деление на который поворачивает вектор, изображающий комплексное число, на угол против и по часовой стрелке, соответственно. Если учесть, что

; ,

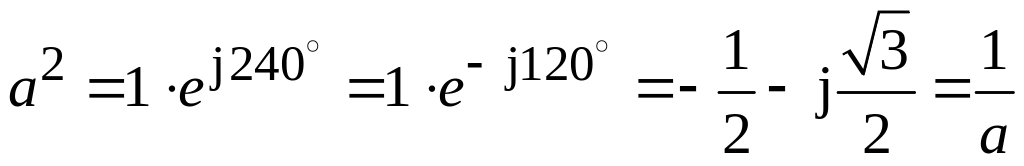то комплексы ЭДС будут равны:

; ; , где .

Поскольку , то и .

Порядок, в котором ЭДС проходят через максимум, называется последовательностью фаз или порядком чередования фаз. При направлении вращения, указанном на рис. 8.1, получается последовательность АВС, которая называется прямой (рис. 8.2). Если изменить направление вращения на противоположное, то получится обратная последовательность.

Трехфазная система ЭДС одинаковой амплитуды, сдвинутых по фазе на один и тот же угол, называется симметричной.

Трехфазной цепью называется совокупность трех цепей, электрически связанных между собой, в каждой из которых действует одна из ЭДС трехфазной системы.

Каждая из этих цепей называется фазой. Так что в электротехнике термин «фаза» имеет два различных по смыслу значения: или аргумент синусоидальной величины, характеризующей периодический процесс, или наименование части трехфазной (а в общем случае – многофазной) цепи.

Фазы цепи обозначаются на схемах латинскими буквами A, B, C, а в энергосистемах различаются по цветам: желтый, зеленый и красный, в которые выкрашены соответствующие шины на электрических станциях и подстанциях. На рис. 8.3 показана несвязанная цепь, в которой каждая из фаз работает независимо от остальных.

Если комплексные сопротивления фаз нагрузки одинаковы

,

то такая нагрузка называется симметричной. Если к тому же симметрична и система ЭДС, то система токов также будет симметричной: . Тогда и нет смысла прокладывать три обратных провода от приемника к источнику. Проще сохранить лишь один провод на случай, когда нагрузка фаз станет различной, а в номинальном режиме постараться распределить нагрузку между фазами равномерно. В результате получается трехфазная цепь, соединенная звездой (рис. 8.4,а).

Здесь узлы N и n называются нейтралями, провод Nn – нейтральным или нулевым проводом, а остальные три, соединяющие обмотку генератора с нагрузкой, – линейными проводами. В линейных проводах протекают линейные токи, между ними возникают линейные (междуфазные) напряжения, в фазах нагрузки и генератора текут фазные токи, на них возникают фазные напряжения.

Очевидно, в рассматриваемой схеме понятия линейный и фазный токи относятся к одному и тому же току. А линейное и фазное напряжения связаны вторым законом Кирхгофа:

Другой вариант связанной цепи – соединение источника и приемника треугольником (рис. 8.4,б). Здесь одинаковы линейное и фазное напряжения, а линейный и фазный токи связаны первым законом Кирхгофа:

В обоих случаях экономится цветной металл (три–четыре провода вместо шести при несвязанной цепи).

В системе без нейтрального провода источник и приемник могут иметь различные соединения.