Модель Леонтьева.

Линейное программирование.

Контрольные задания для самостоятельной учебной работы студентов по дисциплине “ЭКОНОМИКО- МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ”

Автор - доцент кафедры информатики и математики СПбГУП, кандидат физико-математических наук, доцент Махов А.М.

Для студентов экономических и управленческих специальностей

Санкт-Петербург

1998

__________________

Для использования навигации по оглавлению рекомендуется в MS Word использовать режим просмотра схемы документа («Вид» - «Схема документа»)

Пояснительная записка.

Согласно программе дисциплины “Математическое моделирование в экономике” студенты должны выполнить индивидуальное домашнее задание. Оно состоит из двух частей: расчёта баланса в модели Леонтьева и решения задачи линейного программирования.

Первое задание может быть выполнено в электронном виде с использованием приложения MS Excel - файл примера Balance.xls, для второго – файл примера Linprogr.xls.

Задание 1. Модель “затраты- выпуск” (модель в.Леонтьева).

1. Индивидуальное задание.

Произвести расчёт баланса в модели Леонтьева для четырёх- отраслевого народного хозяйства. Матрица структурных коэффициентов должна быть получена каждым студентом самостоятельно из порядковых номеров букв его фамилии и инициалов. Полученными числами необходимо построчно заполнить матрицу (4 x 4), а затем разделить каждый элемент матрицы на 200. Порядковые номера букв можно определить из следующей таблицы:

Буква	А	Б	В	Г	Д	Е	Ё	Ж	З	И	Й
ее номер	1	2	3	4	5	6	7	8	9	10	11
Буква	К	Л	М	Н	О	П	Р	С	Т	У	Ф
ее номер	12	13	14	15	16	17	18	19	20	21	22
Буква	Х	Ц	Ч	Ш	Щ	Ъ	Ы	Ь	Э	Ю	Я
ее номер	23	24	25	26	27	28	29	30	31	32	33

Пример построения матрицы структурных коэффициентов для Сидорова И. П.:

С И Д О 19 10 5 16 0,095 0,050 0,025 0,080

Р О В И 18 16 3 10 0,090 0,080 0,015 0,050

П С И Д  17 19 10 5  0,085 0,095 0,050 0,025 = А

О Р О В 16 18 16 3 0,080 0,090 0,080 0,015

Для определенности нужно считать в полученной матрице первую отрасль сельским хозяйством, производящим продукцию, измеряемую тоннами; вторую отрасль – добывающей промышленностью, производящей продукцию, измеряемую тоннами; третью отрасль – машиностроением, производящим машины, количество которых измеряется в штуках; четвёртую – лёгкой промышленностью, производящей товары народного потребления (измеряются в штуках).

Вектор годового объёма конечного потребления получается также из фамилии студента, но его элементы умножаются на 100000, 10000, 10000, 1000000, соответственно. Пример построения вектора конечного потребления для Сидорова И. П.:

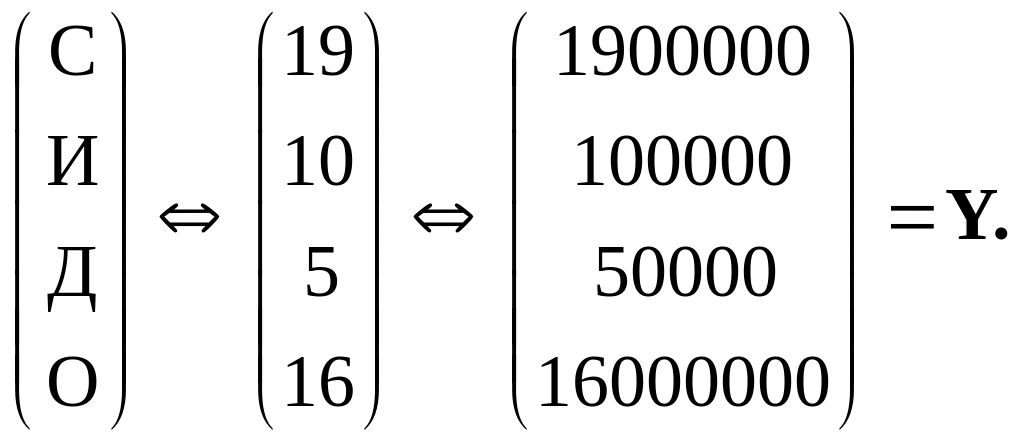
Вектор объёма трудозатрат на единицу продукции и стоимость человекочаса одинаковы для всех и, соответственно, равны: 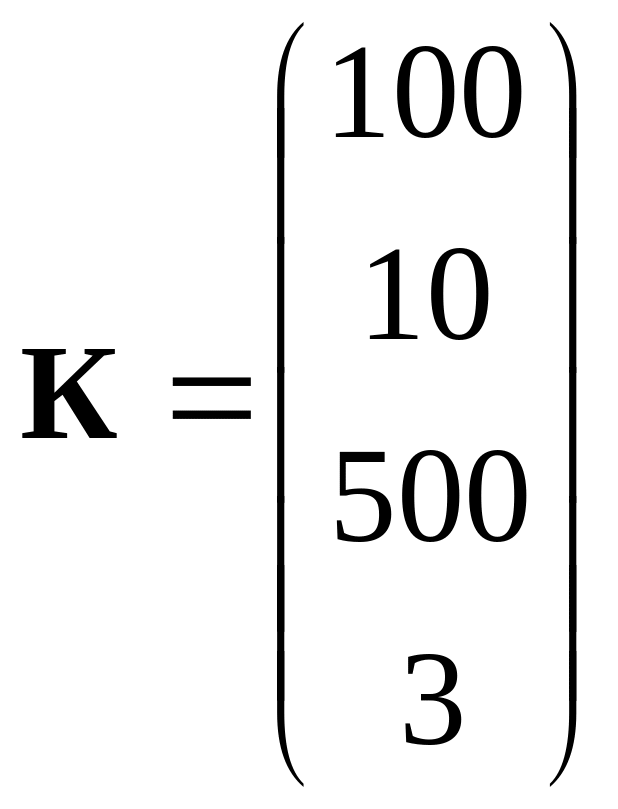человекочасов на единицу продукции, w=$5.

В рассматриваемом обществе действует 40 часовая рабочая неделя, 4 недели в году – отпуск.

2. Порядок выполнения работы

1. составить уравнения межотраслевого баланса в натуральном выражении;

2. пояснить экономический смысл всех структурных коэффициентов a_ij;

3. найти матрицу (Е-А)^-1;

4. найти вектор полного объема производства и вектор цен;

5. найти полный объём трудозатрат и численность занятых в производстве;

6. составить отчёт, содержащий результаты выполнения пунктов 1) - 5).