[Править]Применения закона Кирхгофа [править]в астрофизике

В астрофизике закон Кирхгофа часто применяется в следующем виде:

,

где   — коэффициент излучения (энергия, излучаемая единичным объёмом в единичном интервале частот в единичный телесный угол за единицу времени);   — коэффициент поглощения с учётом вынужденного испускания ( , где   — плотность вещества, а   и   — соответственно непрозрачность и эффективная длина пробега фотонов для частоты  );   — интенсивность излучения абсолютно чёрного тела.

Закон Кирхгофа справедлив только для случаев теплового равновесия. Однако, его часто применяют и для неравновесных систем, когда излучение не находится в равновесии с веществом и его распределение по частотам существенно отличается от планковского. При этом часто (но не всегда) предположение о термодинамическом равновесии между частицами излучающего вещества оказывается хорошим приближением. Степень отклонения от закона Кирхгофа может служить мерой отличия излучения космических объектов от теплового.

Закон смещения Вина

[править]

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 ноября 2012; проверки требуют 3 правки.

Кривые потока излучения абсолютно чёрных тел с разной температурой. Наглядно можно увидеть, что возрастании температуры максимум излучения сдвигается в ультрафиолетовую часть спектра (в область коротких длин волн). Именно эту особенность и описывает закон Вина.

Зако́н смеще́ния Ви́на даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.

Содержание [убрать] 1 Общий вид закона смещения Вина 2 Вывод закона 3 Примеры 4 История 5 См. также 6 Ссылки 7 Источники и примечания

[Править]Общий вид закона смещения Вина

λ_max = b/T ≈ 0,002898 м·К × T ⁻¹ (K),

где T — температура, а λ_max — длина волны с максимальной интенсивностью. Коэффициент b, называемый постоянной Вина, в системе СИ имеет значение 0,002898 м·К.

Для частоты света   (в герцах) закон смещения Вина имеет вид:

где

α ≈ 2,821439… Гц/К — постоянная величина,

k — постоянная Больцмана,

h — постоянная Планка,

T — температура (в кельвинах).

[Править]Вывод закона

Для вывода можно использовать выражение закона излучения Планка для абсолютно чёрного тела, записанного для длин волн:

Чтобы найти экстремумы этой функции в зависимости от длины волны, её следует продифференцировать по   и приравнять дифференциал к нулю:

Из этой формулы сразу можно определить, что производная приближается к нулю, когда   или когда  , что выполняется при  . Однако, оба эти случая дают минимум функции Планка  , которая для указанных длин волн достигает своего нуля (см. рисунок вверху). Поэтому анализ следует продолжить лишь с третьим возможным случаем, когда

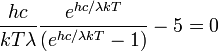
Используя замену переменных  , данное уравнение можно преобразовать к виду

Численное решение этого уравнения даёт:^[1]

Таким образом, используя замену переменных и значения постоянных Планка, Больцмана и скорости света, можно определить длину волны, на которой интенсивность излучения абсолютно чёрного тела достигает своего максимума, как

где температура дана в кельвинах, а   — в метрах.