1)

Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. Иначе говоря, фазы колеба­ний частиц среды и источника тем больше отличаются друг от друга, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т. е. непрерыв­но распределенная в пространстве и обладающая упругими свойствами.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и попереч­ные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны.

Продольные волны могут возбуждаться в средах, в которых возникают упругие силы при деформации сжатия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформации сдвига, т. е. в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как продольные, так и поперечные.

Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис. 220 представлена гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси х, т. е. приведена зависимость между смещением  частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Приведенный график функции (x, t) похож на график гармонического колебания, однако они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний — зависимость смещения данной частицы от времени.

Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны  (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.

или, учитывая, что T= 1/, где  — частота колебаний,

Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси х, а колеблется совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени — один. Волновой фронт также является волновой поверхностью. Волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.

2)

3)

1.3. Интерференция волн. Стоячая волна

Волновые движения малой амплитуды удовлетворяют принцип суперпозиции: две или более волн создают поле, равное сумме их полей. Математически это означает, что такие поля описываются линейными уравнениями, а это значит, что их сумма (суперпозиция) полей тоже описывается линейными уравнениями вида (1.8). Важный частный случай – суперпозиция гармонических волн одинаковой частоты. В тех точках пространства, где поля этих волн колеблются с противоположными фазами (отличающимися на нечетное число ), амплитуда результирующего поля равна разности их амплитуд, а там, где фазы одинаковые или отличаются на четное число  – их сумме. Этот эффект взаимного ослабления или увеличения поля называется интерференцией.

Простым примером интерференции является сложение двух плоских гармонических волн с одинаковыми амплитудами и частотами, распространяющихся навстречу друг другу:

(1.9)

Это уравнение стоячей волны. Такая волна возникает, когда падающая на преграду волна и бегущая ей навстречу отраженная волна налагаются друг на друга.

В уравнении (1.9) видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, а вот амплитуда зависит от координаты х, которую можно рассматривать как расстояние от источника колебаний:

амплитуда =  .

В точках, координаты которых удовлетворяют условию

(1.10)

амплитуда максимальна, а точки называются пучностями стоячей волны. Из формулы (1.10) получаются координаты пучностей

.                                                                             (1.11)

Пучность представляет собой плоскость, точки которой имеют значения координаты х, определяемые формулой (1.11).

В точках, координаты которых удовлетворяют условию

,                                                                          (1.12)

амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны, тогда координаты узлов можно найти:

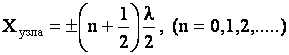.                                                                          (1.13)

Узел тоже представляет не одну точку, а плоскость, точки которой имеют значения координаты х, определяемые по формуле (1.13).

Из формулы (1.11) и (1.13) следует, что расстояние между соседними пучностями и между соседними узлами равно  , а расстояние между соседними пучностями и узлом – .

Вернемся к уравнению (1.9), из которого видно, что при переходе через нулевое значение множитель   меняет знак, что означает, что фаза колебаний по разные стороны узла отличается на , т. е. точки, лежащие по разные стороны от узла колеблются в противофазах (рис. 1.3), а все точки между двумя соседними узлами колеблются в одинаковой фазе.

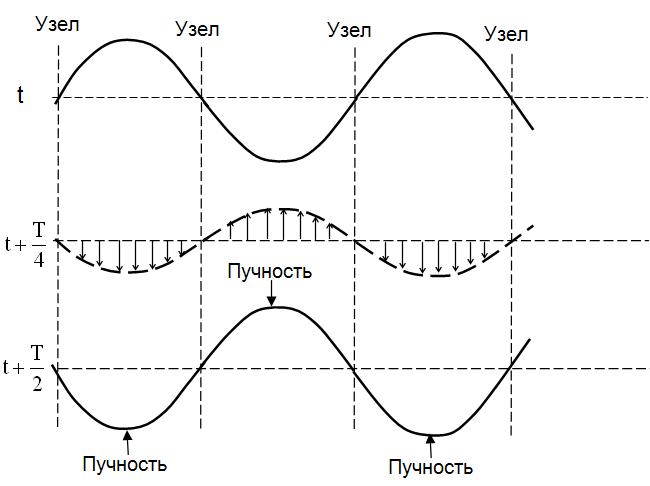
Рис. 1.3. Ряд моментальных фотографий  отклонений точек от положения равновесия

На рис. 1.3 первая «фотография» соответствует моменту наибольшего абсолютного значения отклонения точек от положения равновесия, две другие «фотографии» сделаны через четверть периода. Стрелки показывают направление скорости частиц.

1.4. Звуковая волна

Если частота волн, распространяющихся в упругой среде, лежит в интервале от 16 до 20000 Гц, то, достигнув уха человека, она вызывает ощущение звука. Поэтому такие волны называют звуковыми. Если частота меньше 16 Гц, то это инфразвук, если частота больше 20000 Гц, то –ультразвук.

Всякий реальный звук – это непростое гармоническое колебание, а наложение гармонических колебаний с определенным набором частот. Набор частот колебаний, присутствующих в данном звуке, называют акустическим спектром. Сплошной спектр – в звуке присутствуют все частоты в некотором интервале частот. Линейчатый спектр – звук состоит из колебаний нескольких дискретных частот ₁, ₂, ₃,…..

Звуковая волна в воздухе представляет собой распространяющуюся в пространстве последовательность чередующихся областей сжатия и разрежения газа.

Давление в каждой точке пространства испытывает периодически изменяющееся отклонение   от среднего значения р, совпадающего с давлением, которое существует в газе, когда нет волн. Значит мгновенное значение давления в некоторой точке пространства можно представить:

,

оно приводит к сжатию и расширению соседних участков пространства.

В звуковой волне эти сжатия и расширения газа следуют друг за другом так часто, что смежные участки среды не успевают обмениваться теплом, и процесс можно считать адиабатическим. При адиабатическом процессе связь между давлением  и объемом V данной массы газа дается уравнением

,

где  – отношение теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме. Принимая такую модель, можно получить выражение для определения скорости звуковых волн в газе

,                                                                                                              (1.14)

где р и  – давление и плотность невозмущенного газа.

При атмосферном давлении и обычных температурах большинство газов близко по своим свойствам к идеальному газу. Поэтому можно применить уравнение состояния газа – Менделеева-Клапейрона:

,

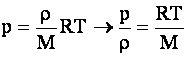тогда скорость звука в газе можно найти:

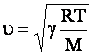,                                                                                                       (1.15)

где R – универсальная газовая постоянная; М – молярная масса газа; Т – температура газа.

Подсчитаем значение скорости звука в воздухе при 290 К (комнатная температура). Для воздуха  = 1,4; М = 2910^-3 кг/моль, R = 8,31  :

.

Найденное значение скорости звука в воздухе хорошо согласуется со значением, полученным опытным путем.

Если создать звуковые колебания в воздушном столбе, то в нем установится стоячая волна, частота которой удовлетворяет определенным условиям, т. е. может принимать только определенные дискретные значения, которые называются собственными частотами колебаний. При колебаниях цилиндрического столба газа в трубе у закрытого конца трубы располагается пучность давления, а у открытого – узел давления.

В любом случае, когда частота колебаний звуковой волны (динамика), совпадает с частотой колебаний воздушного столба, наступает резонанс, который проявляется в возрастании громкости звука.

Интенсивностью звука (силой звука) называется величина, определяемая средней энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны:

Вт/м².

Чувствительность человеческого уха различна для разных частот. Чтобы вызвать звуковое ощущение, волна должна обладать некоторой интенсивностью. Для каждой частоты колебаний существуют наименьший и наибольший порог чувствительности, вызывающий звуковое восприятие. Интенсивность звука – величина объективно характеризующая волновой процесс, а громкость звука – субъективное восприятие процесса. Объективная оценка громкости звука вводится по измеренной интенсивности I:

,                                                                                (1.16)

где I_о – интенсивность звука на пороге слышимости, принимается для всех звуков равной 10^-12 Вт/м²; L – уровень интенсивности звука, выражается в белах, обычно пользуются единицами, в 10 раз меньшими – децибелами (дБ).

Звук еще характеризуется высотой и тембром. Высота звука – качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука, с ростом частоты высота звука увеличивается, т. е. звук становится «выше». Своеобразие звукового ощущения характеризуется тембром звука.

Для акустики помещений большое значение имеет реверберация звука – процесс постепенного затухания звука в закрытых помещениях после выключения его источника. Если в помещении есть звукопоглощающие материалы, то звуки затухают быстро и воспринимаются приглушенно. Время реверберации – время, в течение которого интенсивность звука в помещении ослабляется в миллион раз, а его уровень – на 60 дБ. В помещении хорошая акустика, если время реверберации 0,5–1,5 с.

4)

Оптическое излучение (или свет в широком смысле слова) – это электромагнитные волны, длины которых находятся в диапазоне от 10^-11 до 10^-2 м (от единиц до десятых долей мм) или диапазон частот которых примерно равен 3*10¹¹…3*10¹⁷ Гц.

Как и для любого другого излучения, имеется источник оптического излучения и приёмник оптического излучения. Приёмником оптического излучения, может быть, например, человеческий глаз. Человеческий глаз способен воспринимать оптическое излучение с длиной волны от 400 до 760 нм. Это видимое излучение. Кроме видимого излучения, к оптическому излучению также относятся инфракрасное излучение (с длиной волны от 0,75 до 2000 мкм) иультрафиолетовое излучение (с длиной волны от 10 до 400 нм). Световые волны изучают с помощью оптических методов, которые исторически сложились при анализе законов видимого света.

В 17-м веке были высказаны первые научные гипотезы о природе света. Свет обладает энергией и переносит её в пространстве. Переносить энергию могут либо тела, либо волны, поэтому о природе света вдвинуты две теории.

Корпускулярная теория света (от латинского corpusculum – частица) была предложена в 1672 году английским учёным Исааком Ньютоном (1643 – 1727). Согласно этой теории, свет – это поток частиц, которые во все стороны испускает источник света. С помощью этой теории объяснялись такие оптические явления, как, например, различные цвета излучения.

Голландским учёным Христианом Гюйгенсом (1629 – 1695) также в 17-м веке была созданаволновая теория света, согласно которой свет имеет волновую природу. С помощью этой теории хорошо объясняются такие явления, как интерференция, дифракция света и т.д.

Обе эти теории длительное время существовали параллельно, так как ни одна из них в отдельности не могла полностью объяснить все оптические явления. К началу 19-го века после исследований французского физика Огюстена Жана Френеля (1788 – 1827), английского физика Роберта Гука (1635 – 1703) и других учёных выяснилось, что волновая теория света имеет преимущество перед корпускулярной. В 1801 году английский физик Томас Юнг (1773 – 1829) сформулировал принцип интерференции (усиление или ослабление освещённости при наложении световых волн друг на друга), что позволило ему объяснить цвета тонких плёнок. Френель объяснил, что такое дифракция света (огибание светом препятствий) и прямолинейность распространения света.

И всё же волновая теория света имела один существенный недостаток. В ней предполагалось, что световое излучение представляет собой поперечные механические волны, которые могут возникать только в упругой среде. Поэтому была создана гипотеза о невидимом мировом эфире, который представляет собой гипотетическую среду, заполняющую всю Вселенную (всё пространство между телами и молекулами). Мировой эфир должен был обладать целым рядом противоречивых свойств: должен обладать упругими свойствами твёрдых тел и быть одновременно невесомым. Эти трудности были разрешены во 2-й половине 19-го века при последовательном развитии учения английским физиком Джеймсом Клерком Максвеллом (1831 – 1879) об электромагнитном поле. Максвелл пришёл к вводу, что свет есть частный случай электромагнитных волн.

Однако в начале 20-го века были обнаружены прерывистые, или квантовые свойства света. Этим свойствам давала объяснение корпускулярная теория. Таким образом, свет обладает корпускулярно-волновым дуализмом (двойственностью свойств). В процессе распространения свет обнаруживает волновые свойства (то есть ведёт себя как волна), а при излучении и поглощении – корпускулярные свойства (то есть ведёт себя как поток частиц).

Законы распространения света в прозрачных средах на основе представлений о световом луче рассматриваются в разделе оптики, который называется Геометрическая оптика. Подразумевается, сто световой луч – это линия, вдоль которой распространяется энергия световых электромагнитных волн.

Закон прямолинейного распространения света

На практике свет распространяется прямолинейно внутри ограниченного конуса, который представляет собой световой пучок. Диаметр этого светового пучка превосходит длину световой волны.

Если показатель преломления среды везде одинаков, то такая среда называется оптически однородная среда.

В прозрачной однородной среде свет распространяется прямолинейно. В этом состоит закон прямолинейного распространения света.

Прямолинейность распространения света подтверждается многими явлениями, например, появлением тени от непрозрачных тел. Если S – очень маленький по размеру источник света, а М – непрозрачное тело, преграждающее путь падающему на него свету S, то за телом М образуется конус тени. Свет, идущий от источника, задерживается телом М, и на экране, который помещён под прямым углом к оси конуса, получается хорошо очерченная тень тела М (см. рис. 1.1).

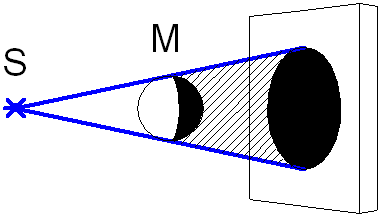Рис. 1.1. Прямолинейность распространения света.

Источники света больших размеров (по сравнению с расстоянием от источников света до препятствия) образуют полутень. Образование полутени можно рассмотреть с помощью двух источников малых размеров, которые находятся друг от друга на расстоянии, равном размеру большого источника света. На рис. 1.2 показано сечение конусов тени, которые образуются светом за телом М. Полная тень образуется позади непрозрачного тела М в той области, куда не попадает свет ни от одного источника света.

Полутень (частично освещённое пространство) образуется в области, где проходят лучи только от одного из источников света. Например, в области, где проходят лучи только источника S1, а другой источник света S2 заслонён телом М. Если источник света большой, то каждая его точка может рассматриваться как точечный источник света. В этом случае будет происходить сложение излучения от отдельных частей излучающей поверхности. Также образуются области тени и полутени.

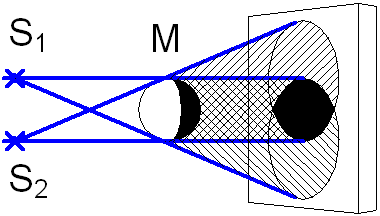Рис. 1.2. Полутень, образованная большим источником света.

Образование тени при падении лучей от источника света на непрозрачный предмет объясняет такие явления, как солнечные и лунные затмения.

Такое свойство, как прямолинейность распространения света, используется при определении расстояний на земле, на море и в воздухе, а также в производстве при контроле по лучу зрения прямолинейности изделий и инструментов.

Прямолинейность распространения света объясняет возможность получения изображений с помощью малого отверстия. Простейшее устройство, позволяющее наблюдать перевёрнутое изображение предметов, называется камера-обскура и представляет собой ящик с небольшим отверстием в передней стенке. Луч света, который распространяется прямолинейно, попадает на заднюю стенку камеры-обскура, где появляется световое пятно с соответствующей интенсивностью. Совокупность световых пятен от всех точек предмета и создаёт изображение этого предмета на задней стенке камеры-обскура.

5)

В основе геометрической оптики лежат законы отражения и преломления света.

Закон отражения утверждает, что отраженный луч лежит в одной плоскости с падающим лучом и нормалью N, проведенной в точке падения, при этом угол отражения равен углу падения. Закон преломления: луч падающий, преломленный и нормаль в точке падения лежат в одной плоскости, отношение синуса угла падения к синусу угла преломления есть величина постоянная для данной пары двух сред и равная относительному показателю преломления второй среды относительно первой.

Если луч распространяется из оптически более плотной среды в менее густое, то при некотором предельном угле падения преломленный луч будет скользить вдоль границы раздела двух сред, т. е. При угле падения световой луч полностью отражается. В этом заключается суть явления полного внутреннего отражения. На явлении полного внутреннего отражения базируется работа приборов (рефрактометров), которые позволяют определять показатель преломления среды.

Линза называется тонкой, если ее толщина d мала по сравнению с радиусами кривизны ее поверхностей R1 и R2. Главной оптической осью линзы называют прямую, проходящую через центры кривизны ее поверхностей. Можно считать, что в такой линзе точки пересечения главной оптической оси с обеими поверхностями линзы совпадают. Эту точку называют центром линзы. Лучи, проходящие через центр линзы, не испытывают преломлений. Плоскости, проходящие через главные фокусы F и линзы перпендикулярно главной оптической оси, называются фокальными плоскостями линзы.

Зачастую бывает, что вещество по обе стороны от линзы одна и та же (например, воздуха). Тогда главные фокусные расстояния численно равны друг другу. Противоположные знаки означают, что главные фокусы лежат по разные стороны от линзы.

6)

Явление обpазования чеpедующихся полос усиления и ослабления интенсивности света называется интеpфеpенцией. Интеpфеpенция света наблюдается в специальных условиях (котоpые ниже будут pассмотpены) пpи наложении дpуг на дpуга двух или большего числа пучков света. Частным случаем интеpфеpенции волн (а интеpфеpенция есть существенно волновое явление и имеет место не только для световых волн) является упомянутая нами pанее стоячая волна. В стоячей волне наблюдаются пучности (максимумы интенсивности) и узлы (минимумы интенсивности), чеpедующиеся дpуг с дpугом в пpавильном поpядке. Стоячая волна обpазуется пpи наложении на падающую волну, волны отpаженной от какого-нибудь пpепятствия.

Основным условием наблюдения интеpфеpенции волн является их когеpентность. Под когеpентностью понимается согласованность волн дpуг с дpугом по фазе. Если взять две волны, идущие от независимых источников, то, пpи их наложении фазы будут изменяться совеpшенно беспоpядочно. Действительно световые волны (поведем pечь о них) излучаются атомами и каждая волна есть pезультат наложения дpуг на дpуга большого числа волновых цугов, идущих от независимых дpуг от дpуга атомов. "Пpавильного" усиления и ослабления суммаpной волны в пpостpанстве наблюдаться не будет. Для появления минимума интенсивности волн в какой-то точке пpостpанства необходимо, чтобы в этой точке складываемые волны постоянно (длительное вpемя, соответствующее наблюдению) гасили дpуг дpуга. Т.е. длительное вpемя волны находились бы точно в пpотивофазе, когда pазность их фаз оставалась бы постоянной и pавнялась  . Наобоpот, максимум волны будет появляться, когда складываемые волны все вpемя находятся в одной и той же фазе, т. е. когда они постоянно усиливают дpуг дpуга. Таким обpазом, интеpфеpенция будет наблюдаться пpи условии, когда накладываемые дpуг на дpуга волны в каждой точке светового поля имеют постоянную во вpемени pазность фаз. Если эта pазность фаз pавна четному числу  , то будет максимум, если нечетному числу  , то будет минимум интенсивности света. Волны с постоянной pазностью фаз называются когеpентными. Можно говоpить о когеpентности волны самой с собой. Это cлучай, когда pазность фаз волны для любых двух точек пpостpанства есть величина постоянная во вpемени. Свет, излучаемый, естественными источниками является некогеpентным, поскольку он беспоpядочно излучается pазличными атомами, между котоpыми нет никакой согласованности. Как же тогда можно наблюдать интеpфеpенцию? Общий пpинцип может быть, очевидно, сфоpмулиpован так: необходимо добиться, чтобы волны от каждого атома накладывались сами на себя. Ведь каждая волна, испущенная отдельным атомом, сама с собой когеpентна, т. к. пpедставляет собой кусок синусоидальной волны. Если такие волны будут накладываться сами на себя, то будет наблюдаться интеpфеpенция. Таким обpазом, общее и пеpвое пpавило наблюдения интеpфеpенции света таково:

Необходимо световой пучок, идущий от одного источника, каким-то обpазом pазделить на два или на большее число пучков (эти пучки будут когеpентны между собой), а затем заставить их наложиться дpуг на дpуга. Максимумы интенсивности волны будут наблюдаться в точках, где выполняется условие

(1.12)

минимумы - в точках, где

(1.13)

Здесь чеpез  обозначена pазность фаз складываемых волн.

Рассмотpим пpимеp интеpфеpенции - опыт Юнга. Допустим, что свет от лампочки со светофильтpом, котоpый создает пpактически монохpоматический свет, пpоходит чеpез две узкие, pядом pасположенные щели, за котоpыми установлен экpан (pис. 1.7). На экpане будет наблюдаться система светлых и темных полос - полос интеpфеpенции. В данном случае единая световая волна pазбивается на две, идущие от pазличных щелей. Эти две волны когеpентны между собой и пpи наложении дpуг на дpуга дают систему максимумов и минимумов интенсивности света в виде темных и светлых полос соответствующего цвета. Где возникнет максимум и где минимум? Рассмотpим какую-нибудь точку экpана М. Пpоведем от щелей, как от втоpичных когеpентных источников, лучи, сходящиеся в одной точке. Найдем pазность хода этих лучей - отpезок  . Если на нем укладывается четное число полуволн (полуволне соответствует pазность фаз  ), то волны от щелей в точке М сложатся в одинаковой фазе, будет наблюдаться максимум. Если на отpезке  укладывается нечетное число полуволн, то они складываются в пpотивофазе и будет наблюдаться минимум. Таким обpазом, условия наблюдения максимумов и минимумов (1.14) и (1.15) можно пpедставить так:

(max),

(1.14)

(min),

(1.15)

Мы pассмотpели пpимеp, когда волны от когеpентных источников (щелей) "бегут" в одной и той же сpеде, с одинаковой скоpостью. Однако в дpугих опытах интеpфеpиpующие волны могут пpоходить pазные сpеды, и как следствие иметь pазные фазовые скоpости. В этом случае вместо геометpической pазности хода удобно говоpить о так называемой оптической pазности хода.

В фоpмулах (1.15) под   следует подpазумевать длину волны света в данной сpеде. Обозначим длину той же волны в вакууме чеpез  . Согласно (1.6) можно записать, что

(1.16)

и, следовательно,

(1.17)

Тогда фоpмулы для интеpфеpенционных максимумов и минимумов (1.15) можно пpедставить в виде:

(max)

(min)

(1.18)

Если интеpфеpиpующие волны пpоходят pазличные сpеды, показатели пpеломления котоpых n1 и n2, то условия максимумов и минимумов нужно записать:

(max)

(min)

(1.19)

где nl называется оптической длиной пути луча, а  оптической pазностью хода лучей.

Таким обpазом, максимумы интеpфеpенции наблюдаются в точках, для котоpых оптическая pазность хода pавна четному числу полуволн, а минимумы - в точках, для котоpых на оптической pазности хода укладывается нечетное число полуволн.

В выводе фоpмул (1.15) и (1.16) мы пpедполагали, что щели для втоpичных волн бесконечно узкие. Конечная шиpина щелей, очевидно, пpиводит к pазмытию максимумов и минимумов. На достаточно шиpоких щелях максимумы будут пеpекpываться, и интеpфеpенция не будет наблюдаться. Игpает pоль и pасстояние между щелями. Оно должно быть достаточно малым: чем оно меньше, тем шиpе каpтина интеpфеpенции.

Интеpфеpенцию можно наблюдать и в белом, т.е. немонохpоматическом, свете. В этом случае каждая полоса будет pадужно окpашена: интеpфеpенция сопpовождается pазложением света на монохpоматические составляющие (чем больше  , тем на большем pасстоянии отстоят максимумы дpуг от дpуга).

7)

.Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Метод зон Френеля. Дифракция на круглом отверстии и диске.

Дифракция – огибание светом препятствия, проникновение света в область геометрической тени.

Принцип Гюйгенса — Френеля: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Дифракция Френеля:

На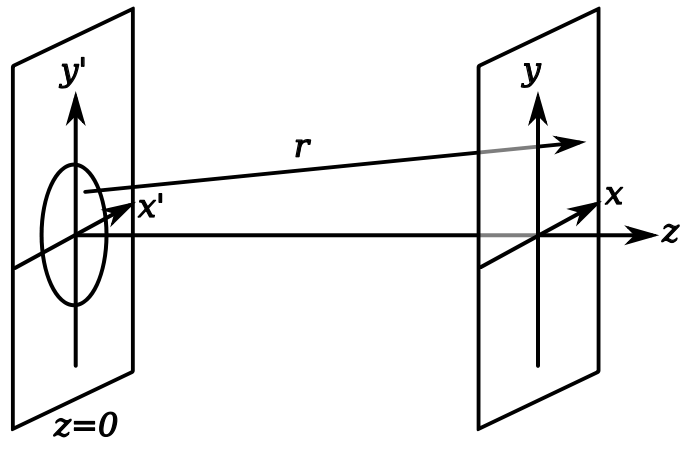 рисунке изображён непрозрачный экран с круглым отверстием, на некотором расстоянии от которого расположен источник света. Изображение фиксируется на другом экране справа. Вследствие дифракции свет, проходящий через отверстие, расходится. Поэтому область, которая была затенена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракция Фраунгофера:

Случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля  , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Метод зон Френеля:

Зоны Френеля - участки, на которые можно разбить поверхность световой волны для вычисления результатов дифракции света.

Суть метода такова. Пусть от светящейся точки   распространяется сферическая волна и требуется определить характеристики волнового процесса, вызванного ею в точке  . Разделим поверхность волны   на кольцевые зоны. Для этого проведём из точки   сферы радиусами  ,  , ,  (  — точка пересечения поверхности волны с линией  ). Кольцеобразные участки поверхности волны, «вырезаемые» из неё этими сферами, и называется зонами Френеля. Волновой процесс в точке   можно рассматривать как результат сложения колебаний, вызываемых в этой точке каждой зоной Френеля в отдельности.

Дифракция Френеля на круглом отверстии:

Сф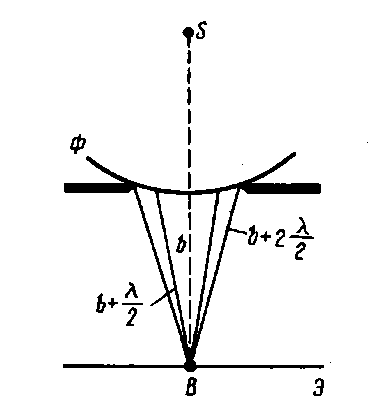 ерическая волна, распространяющаяся из точечного источника  , встречает на своем пути экран с круглым отверстием. Дифракционная картина наблюдается на экране   в точке  . Разобьем часть волновой поверхности   на зоны Френеля. Вид дифракционной картины будет зависеть от количества зон Френеля, укладывающихся в отверстии. Амплитуда результирующего колебания в точке   равна:  (плюс для нечетных  , минус – для четных). Дифракционная картина от круглого отверстия вблизи точки   будет иметь вид чередующихся светлых и темных колец.

Дифракция Френеля на диске:

Сферическая волна, распространяющаяся из точечного источника  , встречает на своем пути диск. Дифракционная картина наблюдается на экране   в точке  . Пусть диск закрывает   первых зон Френеля. Тогда амплитуда результирующего колебания в точке   равна:  .  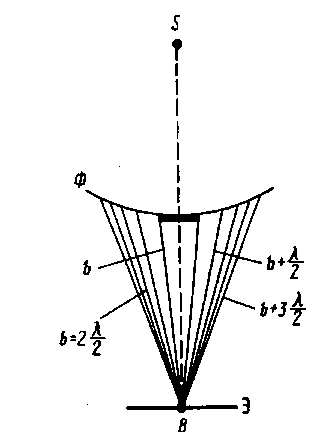Т.к. слагаемое в скобках равно 0, то  . Следовательно, в точке   всегда будет светлое пятно, окруженное концентрическими светлыми и темными кольцами, а интенсивность убывает с расстоянием от центров картины.

8) Дифракция Фраунгофера (или дифракция плоских световых волн, или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию.

Д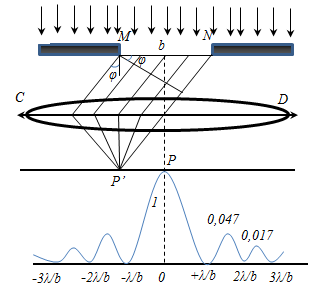 ля наблюдения дифракции Фраунгофера необходимо точечный источник поместить в фокусе собирающей линзы, а дифракционную картину можно исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Пусть монохроматическая волна падает нормально плоскости бесконечно длинной узкой щели ( ), - длина, b - ширина. Разность хода между лучами 1 и 2 в направ­лении φ

Разобьём волновую поверхность на участке щели МN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой полосы выбирается так, чтобы разность хода от краев этих зон была равна λ/2, т.е. всего на ширине щели уложится   зон. Т.к. свет на щель падает нормально, то плоскость щели совпадает с фронтом волны, следовательно, все точки фронта в плоскости щели будут колебаться синфазно. Амплитуды вторичных волн в плоскости щели будут равны, т.к. выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Число зон Френеля   укладывающихся на ширине щели, зависит от угла φ.

Условие минимума при дифракции Френеля:

Если число зон Френеля четное

или

то в т. Р наблюдается дифракционный минимум.

Условие максимума:

Если число зон Френеля нечетное

то наблюдается дифракционный максимум.

При φ’=0, Δ = 0 в щели укладывается одна зона Френеля и, следо­вательно, в т. Р  главный (центральный) максимум нулевого порядка.

Основная часть световой энергии сосредоточена в главном максимуме: m =0:1:2:3...; I=1: 0,047: 0,017: 0,0083... (m -порядок максимума; I- интенсивность).

Сужение щели приводит к уширению главного максимума и уменьшению его яркости (то же и с другими максимумами). При уширении щели (b>λ) максимумы будут ярче, но дифракционные полосы становятся уже, а числе самих полос - больше. При b>> λ центре получается резкое изображение источника света, т.е. имеет место прямолинейное распространение света.

При падении белого света будет разложение на его составляющие. При этом фиолетовый свет будет отклоняться меньше, синий - больше и т.д., красный - максимально. Главный максимум в этой случае будет белого цвета.

§5 Дифракционная решетка.

Д ифракционная решетка представляет собой совокупность большого числа N одинаковых по ширине и параллельных друг другу щелей, разделенных непрозрачными промежутками, также одинаковыми по ширине

b -ширина щели;

а - ширина непрозрачного участка;

d = a + b -период или постоянная решетки.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция. Т.к. щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки.

(1)

В направлениях, в которых наблюдается минимум для одной щели, будут минимумы и в случае N щелей, т.е. условие главных минимумов дифракционной решетки будет аналогично условию минимумов для щели:

(2)

- условие главных минимумов.

Условие максимумов; те случаи φ, которые удовлетворяют максимумам для одной щели, могут быть либо максимумами, либо минимумами, т.к. всё зависит от разности хода между лучами.Условие главных максимумов:

(3)

Эти максимумы будут расположены симметрично относительно центрального (нулевого k = 0) максимума.

Для тех углов φ, для которых одновременно выполняется (2) и (3) максимума не будет, а будет минимум (например, при d =2b для всех четных k =2р, р = 1, 2, 3...). Между главными максимумами имеются дополнительные очень слабые максимумы, интенсивность которых во много раз меньше интенсивности главных максимумов (1/22 интенсивности ближайшего главного максимума). Дополнительных максимумов будет N - 2, где N - число штрихов.

Условие дополнительных максимумов:

Между главными максимума будут располагаться (N-1) дополнительных минимумов.

Условие дополнительных минимумов:

Таким образом, дифракционная картина, при дифракции на дифракционной решетке зависит от N и от отношения d/b.

Пусть N =5,d/b =4. Тогда число главных максимумов(sin φ =1) k_max < d/λ . Между ними по N -2 = 3 дополнительных максимума и N – 1 = 4 дополнительных минимума. При k/m = d/b =2,4,8... - главных максимумов не будет, а будут главные минимумы.

Таким образом, дифракционная картина при дифракции на дифракционной решетке будет иметь вид:

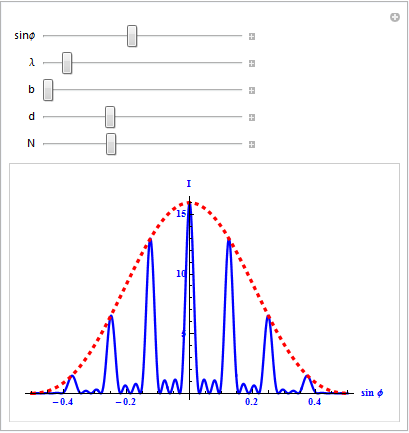
Если решетку освещать монохроматическим белым светом, то будет картина, показанная на рис. Если освещать белым светом, то все максимумы, кроме центрального (k = 0) разложатся в спектр - совокупность составляющих цветов, причем фиолетовые линии будут ближе к центру, а красные дальше (т.к. λ_ф < λ_кр , то φ_ф < φ_кр).

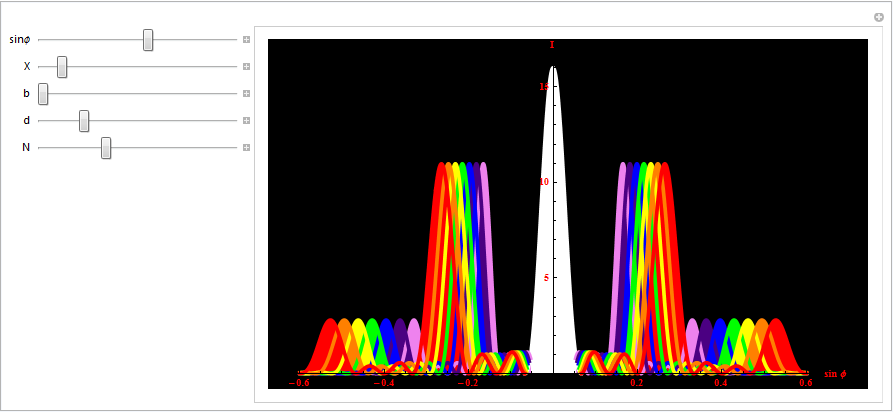
9) Дифракция Фраунгофера на дифракционной решетке

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Рассмотрим дифракционную решетку.

Р ис.33.8. Дифракция света на одномерной плоской решетке.

На рис.33.8 для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d = a+b называется постоянной (периодом) дифракционной решетки.

Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления  одинаковы в пределах всей дифракционной решетки:

(33.16)

Результат интерференции этих лучей на экране зависит от разности фаз складывающихся колебаний. Если она составит   т.е. лучи придут в одной фазе, то они усилят друг друга, если разность хода составит   то лучи ослабят друг друга.

Таким образом, условие максимума для решетки следует записать в виде:

(33.17)

Условие минимума при дифракции на плоской решетке имеет, следовательно, вид:

(33.18)

Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рис.33.9 качественно представлена дифракционная картина от восьми щелей. Так как модуль sin не может быть больше единицы, то из (33.17) следует, что число главных максимумов

т. е. определяется отношением периода решетки к длине волны.

Рис.33.9. Результат дифракции монохроматического света на решетке из 8 щелей.

Положение главных максимумов зависит от длины волны  (см. (33.17)). Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m=0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная - наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т. е. дифракционная решетка может быть использована как спектральный прибор.

Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем штрихов и их частотой (от 6000 до 0,25 штрих/мм, что позволяет перекрывать область спектра от ультрафиолетовой его части до инфракрасной). Например, ступенчатый профиль решетки позволяет концентрировать основную часть падающей энергии в направлении одного определенного ненулевого порядка. Используются высококачественные отражательные решетки и решетки «на просвет».

Дифракция на пространственной решетке. Формула Вульфа - Брэггов

Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения. Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную порядка 10-10 м и, следовательно, непригодны для наблюдения дифракции в видимом свете (  10-7 м). Эти факты позволили немецкому физику М. Лауэ (1879—1960) прийти к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с  рентгеновского излучения ( 10-1210 -8 м).

Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга Г. В. Вульфом (1863—1925) и английскими физиками – отцом Генри и сыном Лоуренсом Брэггами (отец (1862—1942) и сын (1890—1971)). Они предположили, что дифракция рентгеновского излучения является результатом его отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки).

Представим кристаллы в виде совокупности параллельных кристаллографических плоскостей (рис.33.10), отстоящих друг от друга на расстоянии d. Пучок параллельных монохроматических рентгеновских лучей (1, 2) падает под углом скольжения  (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1 и 2', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа — Брэггов

2dsin = m (m = 1,2,3,…), (33.19)

т . с. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн  , наблюдается дифракционный максимум.

Рис.33.10. Дифракция рентгеновских лучей на пространственной (кристаллической) решетке.

При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром» испускаемым рентгеновской трубкой. Тогда для таких условий опыта всегда найдутся длины волн , удовлетворяющие условию (33.19).

Формула Вульфа — Брэггов используется при решении двух важных задач:

1. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристаллической структуре неизвестного строения и измеряя  и m, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества. Этот метод лежит в основе рентгеноструктурного - анализа. Формула Вульфа - Брэггов остается справедливой и при дифракции электронов и нейтронов. Методы исследования структуры вещества, основанные на дифракции электронов и нейтронов, называются соответственно электронографией и нейтронографией. Электронография дает уникальную возможность определить величину параметра решетки (и её изменение вследствие различных воздействий) с ошибкой, не превышающей 210-14 м (!!!). Нейтронография позволяет исследовать такие тонкие явления, как тепловые колебания узлов кристаллической решетки. Правда, для получения достаточного потока нейтронов требуется атомный реактор…

2. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кристаллической структуре при известной d и измеряя  и m, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии и позволяет производить прецизионный спектральный анализ, в том числе пленочных конструкций, хотя пространственное разрешение по современным понятиям оставляет желать лучшего.

Процессы в электрических цепях с сосредоточенными элементами носят колебательный характер и описываются электрическими колебаниями напряжений и токов в различных частях цепи. Эти колебания описывают скалярными функциями времени (t) и обозначают: u(t) - мгновенное значение напряжения, i(t) - мгновенное значение

10)

Дифракционную картину могут дать не только рассмотренные выше одномерные структуры, но также двумерные и трехмерные периодические структуры, например, кристаллические тела. Однако период кристаллических тел d мал, составляет единицы ангстрем (1  =10^-4 мкм), т.е. значительно меньше длин волн видимого света (0,4-0,8 мкм). Поэтому для видимого света кристаллы являются однородной средой, и дифракция не наблюдается.

Рис.6

Вто же время для значительно более коротковолнового рентгеновского излучения( 10-9 - 10-11 м) кристаллы представляют собой естественные дифракционные решетки (см. рис.6). Абсолютный показатель преломления всех среддля рентгеновского излучения близок к единице, поэтому оптическая разность хода между лучами

1- и 2-, отражающимися от кристаллографических плоскостей CD+DE=2dsin, где d - расстояние между плоскостями, в которых лежат узлы (атомы) кристаллической решетки,  - угол скольжения лучей.

Условию интерференционных максимумов удовлетворяет [см.(3,15)] формула Вульфа-Брэгга

2dsin =m , m=1,2,3- (13)

где m - порядок дифракционного максимума.