1.7 Расчет спирального отвода

1.7.1 Расчет отвода

Определим ширину отвода, [м]:

(7.1.1)

.

Найдем радиус расположения языка отвода, [м]:

(7.1.2)

.

Радиальный зазор между колесом и языком отвода, [м], определяем по формуле:

(7.1.3)

.

Угол атаки языка отвода принимаем:

Определяем угол языка отвода:

(7.1.4)

.

Принимаем отношение скоростей Ξ = С_г/С_2u = 0,65 откуда скорость потока в горле, [м/с]:

(7.1.5)

Найдем площадь горла, [м²]:

(7.1.6)

Вычислим эквивалентный диаметр горла, [м]:

(7.1.7)

.

Определяем высоту горла для прямоугольного сечения сборника, [м]:

(7.1.8)

.

Предварительно принимаем скорость потока на выходе из насоса, [м/с]:

(7.1.9)

Найдем площадь выходного сечения диффузора (напорного патрубка), [м²]:

(7.1.10)

Диаметр выходного сечения диффузора (напорного патрубка) , [м], рассчитаем по формуле:

(7.1.11)

.

Полученное значение округляем до ближайшего из стандартного ряда диаметров фланцев .

Уточняем и по формулам:

(7.1.12)

.

(7.1.13)

Длина конического диффузора должна удовлетворять условию:

Предварительно принимаем:

(7.1.14)

Находим эквивалентный угол кон. диффузора (опт. значение в пределах 6…10):

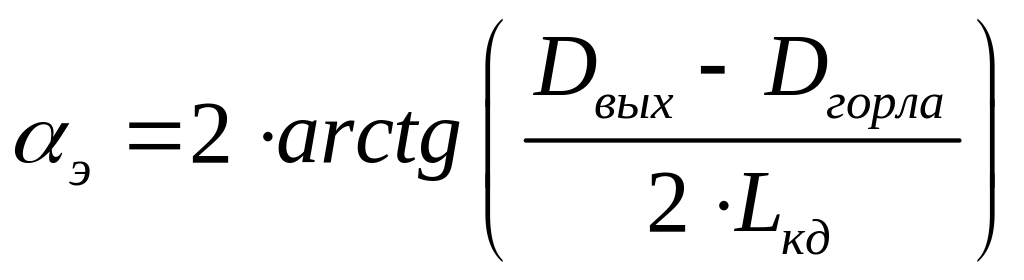(7.1.15)

1.7.2 Потери в спиральном отводе

Уравнение логарифмической спирали в полярных координатах (по 7 точкам, i=1…7):

(7.2.1)

(7.2.2)

Площадь поперечного сечения и смачиваемый периметр спирального сборника, [м²], [м]:

(7.2.3)

(7.2.4)

Определим эти параметры для семи точек, сведем данные в таблицу 1:

1	0.100786	0.114823	0.000244	0.050297
2	1.131186	0.127434	0.000713	0.075518
3	2.161586	0.14143	0.001233	0.10351
4	3.191986	0.156962	0.001809	0.134575
5	4.222386	0.174201	0.00245	0.169052
6	5.252785	0.19333	0.00316	0.207315
7	6.283185	0.214566	0.003949	0.249781

Вычислим диаметр трубы того же гидравлического радиуса для любого сечения спирали, [м]:

(7.2.5)

	1	2	3	4	5	6	7
	0,019405	0,037766	0,047648	0.053769	0.05797	0.06097	0.063239

Определяем средний гидравлический диаметр спирали, [м]:

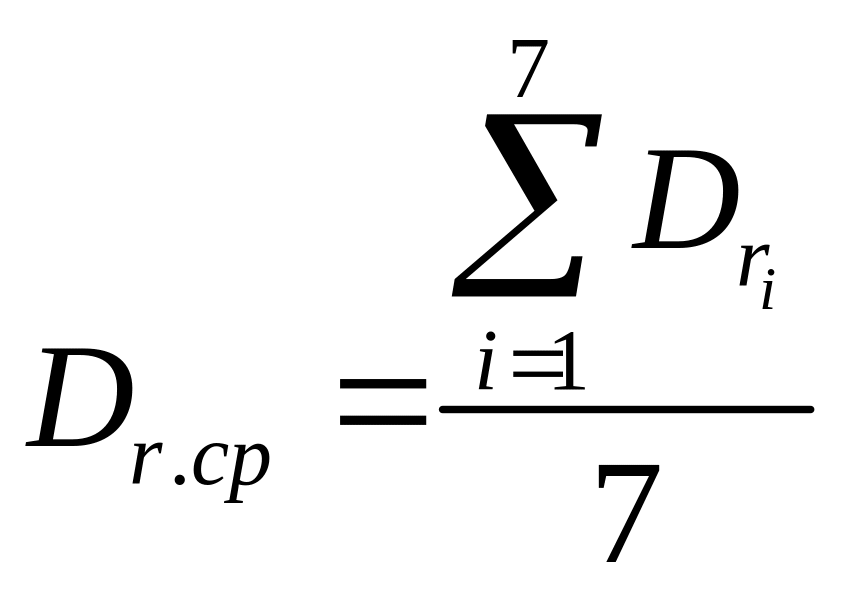(7.2.6)

Средняя скорость движения в спиральном сборнике, [м/с], рассчитается по формуле:

(7.2.7)

За длину эквивалентного трубопровода принимаем половину длины спирали.

Находим длину спирали, [м]:

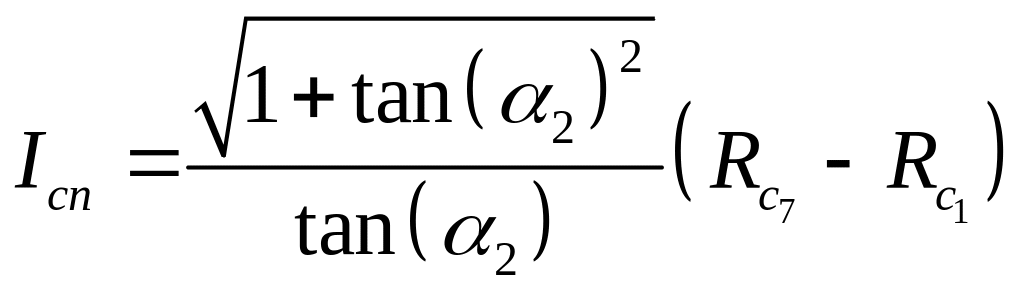(7.2.8)

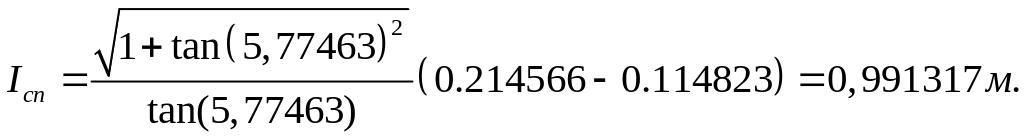
Определим число Рейнольдса по средней скоростью в спиральном диффузоре:

(7.2.9)

Вычислим эквивалентную шероховатость [с], т.е. такую равномерную шероховатость, которая дает при подсчете одинаковую с заданной шероховатостью величину :

(7.2.10)

Гидравлический коэффициент трения (коэффициент Дарси) для трех областей гидравлических сопротивлений, если 10< <500 (переходная область) будет рассчитан по формуле:

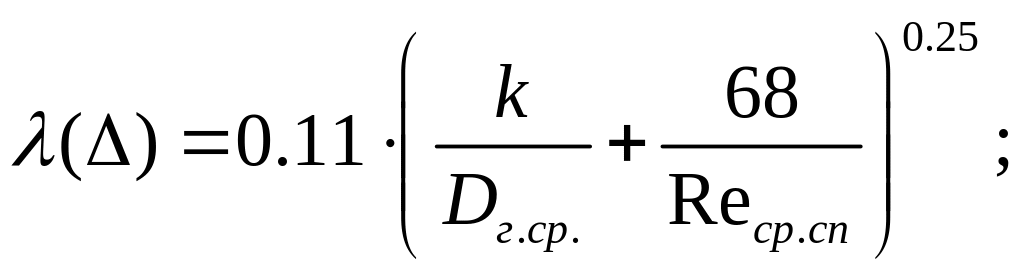(7.2.11)

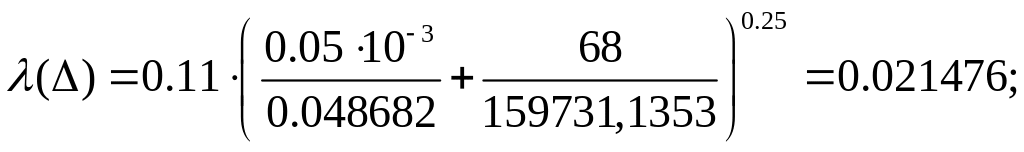
Найдем потери на трение о стенки в спиральном сборнике, [м]:

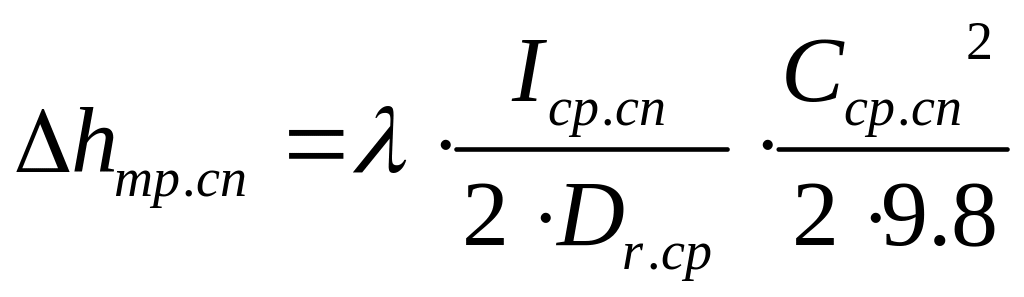(7.2.12)

Определяем потери энергии, связанные с внезапным изменением скорости - ударные потери, [м]:

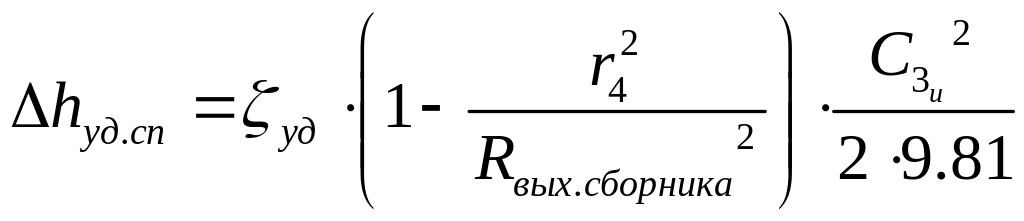(7.2.13)

где - радиус на выходе из спирального сборника;

- выбирается из (0.3…0.5).