МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра общей и теоретической физики

Изучение законов геометрической оптики

Методические указания

по выполнению лабораторных работ

для студентов 2 курса

Издательство "Самарский университет"

2005

Изучение законов геометрической оптики Теоретические основы эксперимента

1. Геометрическая (лучевая) оптика

Согласно электромагнитной теории диапазон видимого света представляет собой электромагнитные волны определенной длины : от 4,010^-5 см до 7,510^-5 см . С помощью волновой теории можно решать задачи о распространении света как в однородной среде, так и через любую оптическую систему, т.е. через совокупность различных сред, ограниченных теми или иными поверхностями и диафрагмами. Однако в очень многих областях, имеющих важное практическое значение, в частности, в вопросах о формировании светового пучка (светотехника) и в вопросах об образовании изображения (оптотехника), решение можно получить гораздо более простым путем, с помощью представлений геометрической (лучевой) оптики.

Геометрическая оптика оперирует понятием световых лучей, подчиняющихся известным законам преломления и отражения и независимых друг от друга. Понятие светового луча можно получить, рассматривая в однородной среде реальный световой пучок, из которого при помощи одной или нескольких диафрагм с отверстиями выделяется узкий параллельный пучок. В пределе, переходя к отверстиям сколь угодно малым, можно казалось бы получить световой луч как прямую линию. Однако подобный процесс невозможен вследствие явления дифракции: при определенном соотношении длины волны и размера отверстия неизбежно происходит угловое расширение реального светового пучка. Поэтому только в предельном случае, когда  = 0, дифракция не имела бы места, и можно было бы говорить о луче как о геометрической линии, направление которой определяет направление перемещения световой энергии. Поэтому световой луч есть математическая абстракция, а не физический образ, и необходимо понимать волновой смысл всех лучевых (геометрических) построений. Таким образом геометрическая оптика – это предельный случай реальной волновой оптики, соответствующий исчезающе малой длине световой волны, а законы лучевой оптики имеют весьма ограниченное применение.

2. Принцип Ферма. Законы отражения и преломления света

В волновой теории доказывается следующее важное положение: действительный путь распространения света есть путь, для прохождения которого свету требуется минимальное время по сравнению с любым другим мыслимым путем между теми же точками. Этот принцип был сформулирован Ферма (около 1660 г.) как общий закон распространения света. В приближении геометрической оптики данное утверждение является аксиомой (принципом кратчайшего оптического пути). Действительно, для однородной среды принцип Ферма приводит к закону прямолинейного распространения согласно геометрической аксиоме о том, что прямая есть кратчайшее расстояние между двумя точками. Если же свет переходит через границу различных сред, то этот принцип приводит к законам отражения и преломления света.

Пусть свет, исходя из точки Р, приходит в точку Q, преломляясь на плоской границе раздела двух сред (рис.1). Проведем через Р и Q плоскость нормально к границе раздела (плоскость падения). Согласно принципу Ферма действительный путь РОQ меньше любого другого пути, лежащего вне плоскости падения, например, пути РО₁Q, проведенного так, что точка О является следом перпендикуляра, опущенного из точки О₁ на плоскость падения. Следовательно, путь РОQ требует минимального времени. Исследуем, как меняется это время в зависимости от положения точки О .

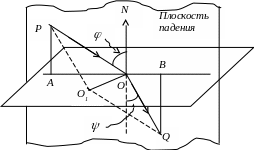
Рис.1. К выводу закона преломления

Положение точки О определено длиной отрезка АО = x , где А – след перпендикуляра, опущенного из Р на плоскость раздела. Время распространения света по пути РОQ есть

где v₁ и v₂ – скорости света в первой и во второй средах. Обозначив РА = h₁, QB = h₂ и AB = a, найдем, что