2. Решение дифракционных задач графическим способом

Итак, вычисление результирующего светового поля производится суммированием световых колебаний, возбуждаемых вторичными источниками. С математической точки зрения задача сводится к сложению гармонических волн, имеющих одну и ту же частоту, но разные амплитуды и фазы. Один из наглядных и изящных способов решения такой задачи – построение векторной диаграммы.

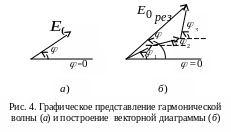
Известно, что гармоническую волну в произвольный момент времени можно представить в виде вектора амплитуды , повернутого на фазовый угол  (рис.4, а). Сумма нескольких гармонических волн частоты  есть также гармоническая волна той же частоты. Амплитуду результирующей волны и фазу можно найти, используя правила сложения векторных величин. На рис.4, б показано сложение трех гармонических волн одинаковой частоты.

Применим метод векторной диаграммы для расчета результирующей амплитуды дифракционного светового поля. Сначала вычислим амплитуду волны, приходящей в точку наблюдения от одной центральной зоны Френеля. Для этого мысленно разобьем эту зону на несколько (например, на шесть) концентрических кольцевых подзон. Если площади подзон считать примерно одинаковыми, то их вклады в освещенность выбранной точки будут изображаться векторами одинаковой длины, но с разными углами наклона к горизонтальной оси. Поскольку центр зоны и ее край посылают волны с разностью фаз  , то все векторы амплитуд волн, испускаемых подзонами, должны быть повернуты друг относительно друга на угол   6. Суммарный вектор представляет результирующую амплитуды волны, идущей от первой зоны Френеля (рис.5, а). Очевидно, разбиение зоны можно произвести на сколь угодно большое число подзон. В случае бесконечно большого числа подзон ломаная линия векторной диаграммы будет приближаться к гладкой кривой (рис.5, б).

Аналогичным образом строится вектор, изображающий совместный вклад первых двух зон (рис.5, в). Здесь учтено, что с номером зоны уменьшается ее вклад в суммарное дифракционное поле, т. е.  и результирующая амплитуда отлична от нуля, хотя и очень мала. Продолжая процедуру построения векторной диаграммы для все большего числа зон (например, трех и четырех на рис.5, г,д), получаем скручивающуюся спираль. Нетрудно видеть, что в предельном случае, когда открыты все зоны Френеля, т. е. свет идет свободно, векторная диаграмма имеет вид гладкой скручивающейся спирали – спирали Френеля (рис.5, е). В этом случае результирующая амплитуда равна половине амплитуды волны, приходящей в точку наблюдения от центральной зоны Френеля. Этот результат совпадает с выводом (5).

3. Дифракция на круглом отверстии и круглом диске

Метод зон Френеля позволяет на качественном уровне объяснить целый ряд дифракционных явлений: дифракцию на отверстии, дифракцию на диске, дифракцию на краю экрана. При этом в основе рассуждений лежит гипотеза, предложенная Френелем: часть волнового фронта световой волны, закрытая непрозрачным экраном, не действует совсем, а неприкрытые участки фронта действуют так, как если бы экрана совсем не было. Гипотеза эта не самоочевидна и в непосредственной близости к краям отверстий не вполне верна. Однако для большинства практически интересных случаев, когда размеры отверстия значительно больше длины световой волны, метод Френеля достаточно хорошо описывает явления дифракции.

Пусть волна, идущая от S встречает на пути экран MN с круглым отверстием (рис.6). Исследуем явление в точке P , лежащей на линии, соединяющей S с центром отверстия. Вспомогательная поверхность  будет касаться экрана MN . Разбивка этой поверхности на зоны Френеля пок ажет, что в зависимости от размера отверстия в нем уложится большее или меньшее число зон. Используя знакопеременный ряд (4), легко убедиться в том, что если отверстие открывает всего лишь одну зону или небольшое нечетное число зон, то амплитуда волны, приходящей в точку Р, будет больше, чем в отсутствие экрана. Максимум действия соответствует размеру отверстия в одну зону. Если же отверстие открывает четное число зон, то световое возбуждение в точке Р будет меньше, чем при свободно идущей волне. Наименьшая освещенность соответствует двум открытым зонам Френеля. Применяя графический метод, получим диаграммы, подобные изображенным на рис. 5.

А налогичные рассуждения применимы для любой точки, лежащей на линии SP . Расчет картины для точек, лежащих в плоскости, перпендикулярной к SP, но в стороне от этой линии, несколько сложнее. Тем не менее, легко видеть, что для любого места выше или ниже, например, точки Р, зоны Френеля на вспомогательной поверхности  будут перестраиваться. По мере удаления от точки Р число зон, укладывающихся в отверстие, будет, вообще говоря, другим. Вследствие симметрии расположения вокруг линии SP , области одинаковой освещенности должны располагаться кольцеобразно около точки Р . При подходящих условиях опыта можно наблюдать несколько концентрических областей максимумов и минимумов освещенности, плавно переходящих друг в друга.

Е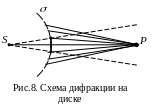 ще более удивительные результаты можно получить, исследуя дифракцию света на круглом непрозрачном экране. Схема дифракции показана на рис. 8. Световая волна падает на круглый непрозрачный диск, а наблюдение поля ведется в некоторой точке Р , расположенной в области геометрической тени на оси диска.

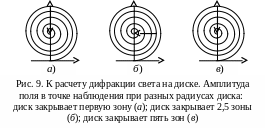
Построение векторов результирующей амплитуды поля с помощью спирали Френеля показано на рис. 9. Из рисунка видно, что даже в случае достаточно большого экрана, закрывающего сразу несколько зон Френеля, интенсивность света в центре геометрической тени отлична от нуля.

В свое время этот результат рассматривался как аргумент против теории Френеля. Однако эксперименты, выполненные Домеником Араго в начале ХIХ в., показали, что в центре геометрической тени от непрозрачного диска действительно существует маленькое светлое пятно! (рис. 10). Оно получило название «пятна Пуассона» - по имени автора идеи опыта.