8

Формулы по статистике

Тема 1: Группировка статистических данных

Определение числа групп (если группи-ка по непрер. приз-ку или дискрет. со многими знач-ями)

Определение величины равного интервала:

Тема 2: Абсолютные и относительные величины

Относительные величины:

1) относит. вел-на структуры:

2) относит. вел-на планового задания:

3) относит. вел-на выполнения плана:

4) относит. вел-на динамики или темп роста:

5) относит. вел-на сравнения

6) относит. вел-на интенсивности (пример: фондоотдача = объем/стоимость (один год))

Тема 3: Средние величины и показатели вариации

Средняя арифметическая

простая:

взвешенная:

Средняя гармоническая

простая:

взвешенная: , сумма значений признака по группе

Свойства средн. арифметической:

1. если каждую вари-ту х умен-ть или увел-ть на одно и то же число, то ср. вел-на умен-ется или увел-ется на это же число;

2. если каждую вари-ту х умен-ть или увел-ть в одно и то же число раз, то ср. вел-на умен-ется или увел-ется в одно и то же число раз;

3. если каждую частоту f умен-ть или увел-ть в одно и то же число раз, то ср. вел-на не изменится.

Ср. вел-на зависит от вар-ты х и структуры совок-сти, кот. харак-ется долями d.

Ряд распределения имеет 3 центра:

1) ср. аримет-кое;

2) мода – наиболее часто встречающаяся вар-та [M₀];

3) медиана – вар-та, стоящая в середине ряда распре-ния. Сначала находят N медианы, кот. равен n/2, если число еди-ц совок-сти n – чётное, или , если число еди-ц совок-сти нечетное [M_e].

Осн. пока-ли вариации:

1) размах вариации:

2) ср. линейное отклонение (ср. арифм-кая из абсолют. откл-ний отдел. значений)

Для несгруппир. данных:

Для сгруппир. данных:

3) ср. квадратическое отклонение (хар-ет ср. абсол. откл-ние вар-ты от ср. вел-ны)

Для несгруппир. данных:

Для сгруппир. данных:

4) Дисперсия – квадрат среднеквадр-ного откл-ния

Для несгруппир. данных:

Для сгруппир. данных:

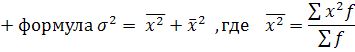
Общая дисперсия: (для сгрупп.) (для несгрупп.)

– ср. вел-на резул. приз-ка в сово-сти, - частота (в совокупности!)

Внутригрупповая дисперсия: - кол-во вариант в группе i

Междугрупповая дисперсия: - кол-во вариант в группе i

Правило сложения дисперсий:

Не имеет еди-ц измерения.

5) Коэффициент вариации хар-ет ср. относит. откл-ние вар-ты от ср. вел-ны.

Способ моментов

Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом.

В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1) Выбирается начало отсчета (из х) – условный нуль (A). Обычно как можно ближе к середине распре-ния.

2) Находятся отклонения вариантов от условного нуля ( ).

4) Если эти отклонения содержат общий множитель (k), то рассчитанные

отклонения делятся на этот множитель.

Способ моментов:

Средняя:

Дисперсия:

Тема 4: Выборочное наблюдение

Обозначения в теории выборки:

N – числи-ль генер. выборки	n – числи-ль генер. выборки
генер. средняя (оценивают)	– выбор. средняя (рассчитывают)
p – генер. доля (оценивают)	w – выбор. доля (рассчитывают)
P(t) – задаваемый уровень веро-сти

Генер. средняя: с задан. уровнем вероя-сти P(t)

– ошибка выборки для ср. вел-ны

, t – критерий надеж-сти, его вел-на зав-т от уровня задан. вероя-сти P(t)

Если 1) P(t) = 0,683, то t=1; 2) P(t) = 0,954, то t=2 ; 3) P(t) = 0,997, то t=3

– среднеквадр. ошибка выборки

– верна для повторного отбора в выборке.

- для бесповторного отбора

Доказано: с задан. уровнем вероя-сти P(t)

– ошибка выборки для доли

, – среднеквадр. ошибка выборки для доли

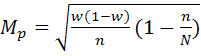–для повторного отбора

- для бесповторного отбора