(1 Биография)

Жан Леро́н Д’Аламбе́р родился 16 ноября 1717 в Париже.

(Д’Аламбер был незаконным сыном маркизы де Тансен от артиллерийского офицера Детуша.)

Вскоре после рождения младенец был подкинут матерью на ступени парижской «Круглой церкви Св. Иоанна» (фр. Église Saint-Jean-le-Rond). В честь этой церкви ребёнок был назван Жаном Лероном. Воспитывался в усыновившей его семье стекольщика Руссо.

Фамилия Д’Аламбер, по одним сведениям, произведена из имени его приёмного отца Аламбера, по другим — придумана самим мальчиком или его опекунами: сначала Жан Лерон был записан в школе как Дарамбер (Daremberg), потом сменил это имя на D’Alembert.

В 1730 поступил в Коллеж четырех наций, по окончании которого (в 1735) получил диплом правоведа. Юриспруденцией впоследствии не занимался, а начал изучать медицину. Оставив и это занятие, решил целиком посвятить себя математике. Уже в возрасте 22 лет Д’Аламбер представил Парижской академии свои сочинения, а в 23 года был избран адъюнктом Академии.( лицо, проходящее научную стажировку, помощникпрофессора.)

Труды

(2 Трактат о динамике )

В 1743 вышел «Трактат о динамике», где сформулирован фундаментальный «Принцип Д’Аламбера».Согласно этому принципу, (если к заданным (активным) силам, действующим на точки механической системы, и реакциям наложенных связей присоединить силы инерции, то получится уравновешенная система сил. Таким образом), уравнениям движения можно придать вид уравнений равновесия, если ко всем точкам системы приложить дополнительно силы инерции.

(Из данного принципа следует, что для каждой i-той точки системы F_a + N + F_ин = 0, где F_a — действующая на эту точку активная сила, N — реакция наложенной на точку связи, F_ин — сила инерции, численно равная произведению массы m_i точки на её ускорение a_i и направленная противоположно этому ускорению (см. второй закон Ньютона).)

В «Трактате о динамике» он впервые сформулировал общие правила составления дифференциальных уравнений движения любых материальных систем.

Позже этот принцип был применен им в трактате «Рассуждения об общей причине ветров» (1774) для обоснования гидродинамики, где он доказал существование — наряду с океанскими — также и воздушных приливов.

(3 исследование задачи о колебаниях струны.)

Основные математические исследования Д’Аламбера относятся к теории дифференциальных уравнений.

Ему принадлежат важные результаты в теории обыкновенных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений 1-го и 2-го порядков.

В 1748 он дал метод решения дифференциального уравнения 2-го порядка в частных производных, описывающего поперечные колебания струны (волнового уравнения). Д’Аламбер представил решение как сумму двух произвольных функций, и по т. н. граничным условиям сумел выразить одну из них через другую.

(Исходное уравнение

Приводится к виду

Преобразованное уравнение легко решается двумя последовательными интегрированиями (сначала по переменной η , а затем по ξ), а общее решение U(ξ,η) имеет вид

или

после подстановки краевых условий получим систему уравнений:

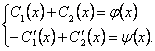
В результате получим решение исходной задачи Коши

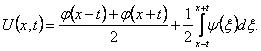
Эта формула называется формулой Даламбера.)

Полученная им формула называется формулой Даламбера.

Эти работы Д’Аламбера, а также последующие работы Л. Эйлера и Д. Бернулли составили основу математической физики.

http://vicaref.mgsu.ru/PDE/index6.htm