Открываем вновь сборку дирижабля Сборка 1 и с помощью последовательностиВставка– Компонент - Из файла вставляем деталь Гондола в эту сборку (рис.2.16).
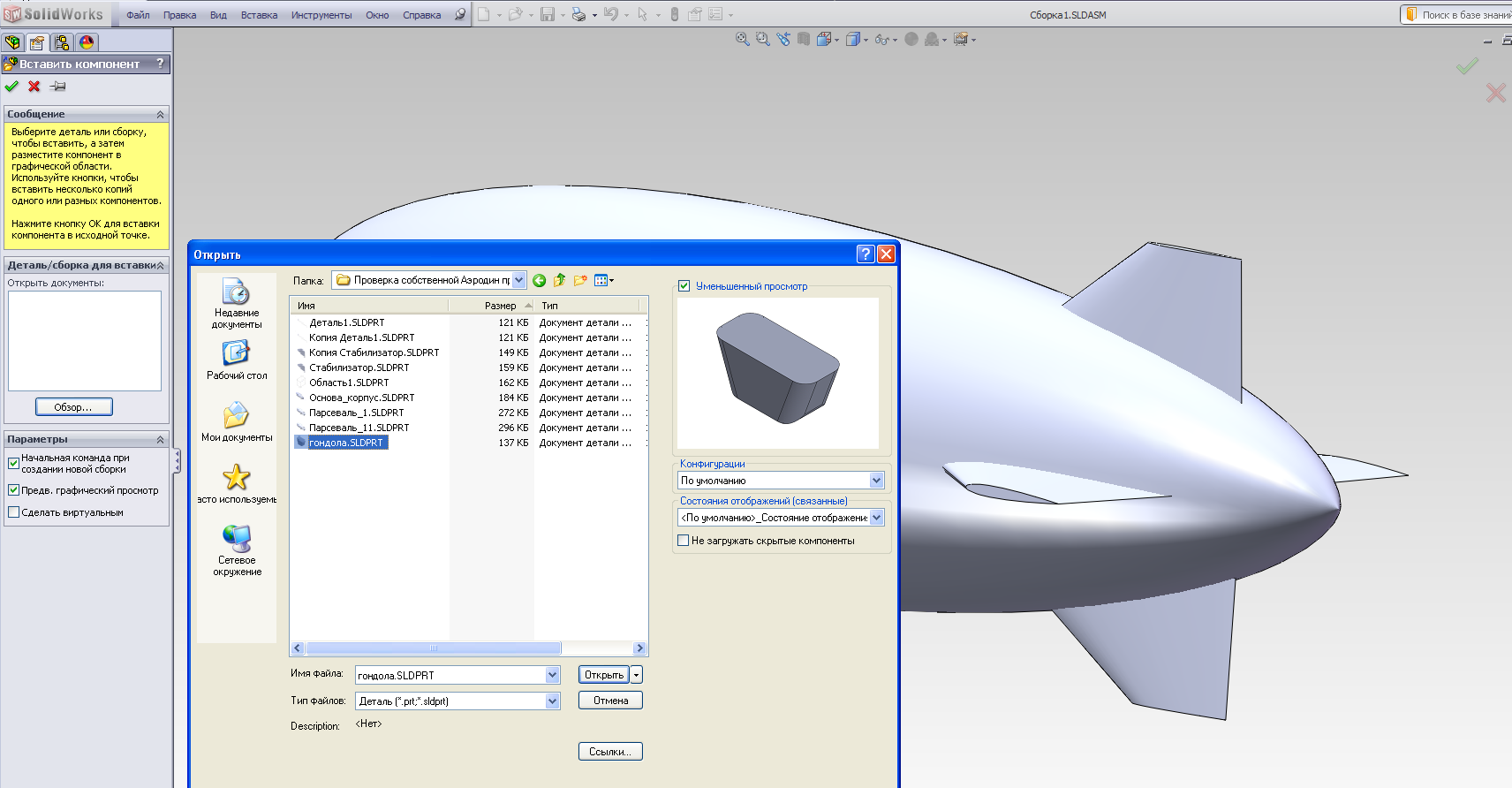
а)
б)
Рис.2.16
Для точного ориентирования гондолы относительно корпуса дирижабля создаем в соответствие с рис.1.2 в дополнительный эскиз (рис.2.17 а), приведенный на рис.2.17 б.
С помощью операцииПереместить с системой координат перемещаем деталь гондолы в искомое положение в плоскости эскиза - руководствуясь отрезками-ориентирами эскиза (рис.2.17 в, г) и далее, - в симметричное положение в поперечной плоскости (рис.2.17 д). В результате получаем полную сборку (рис.2.17 е).
а)
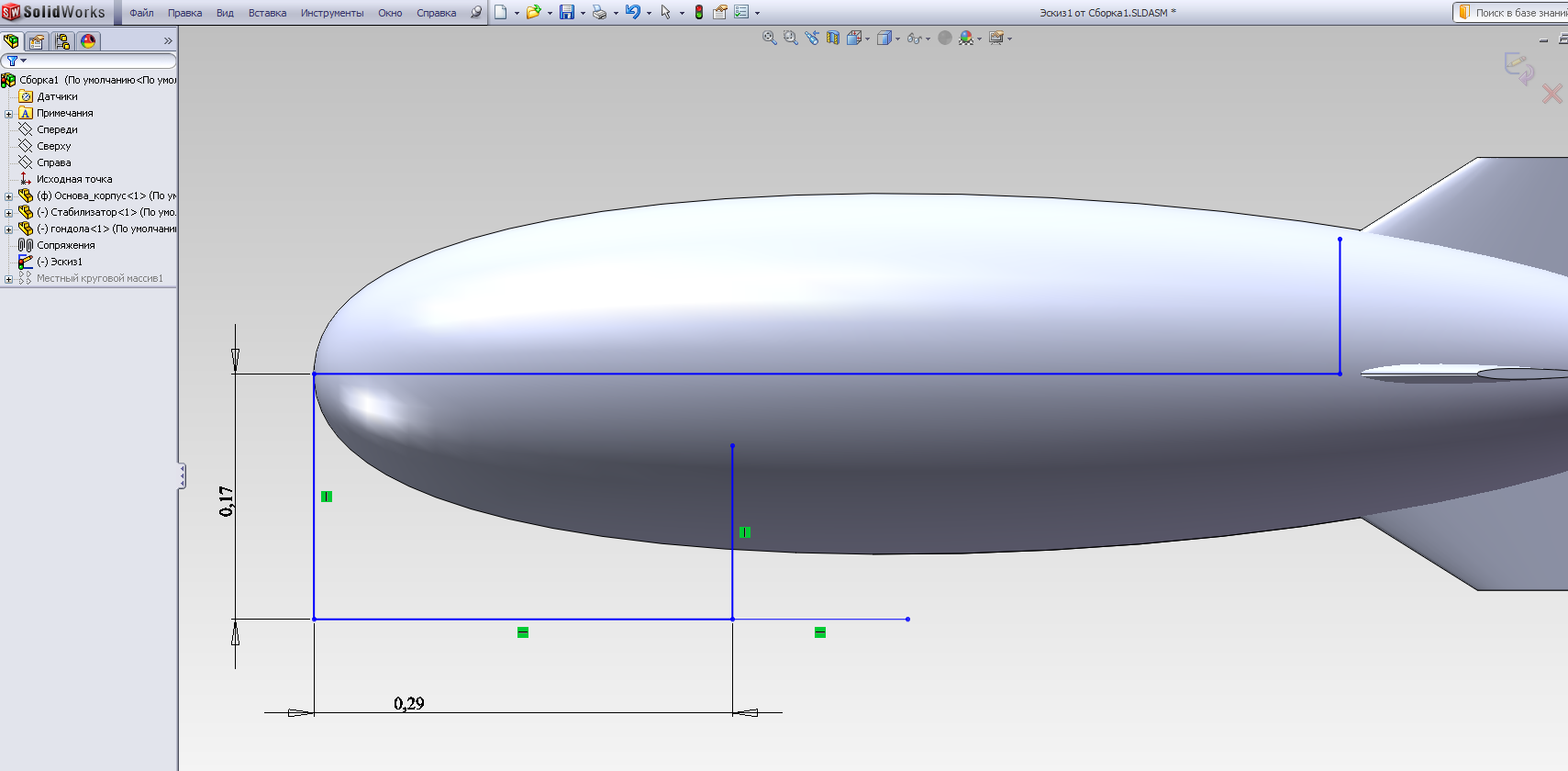
б)
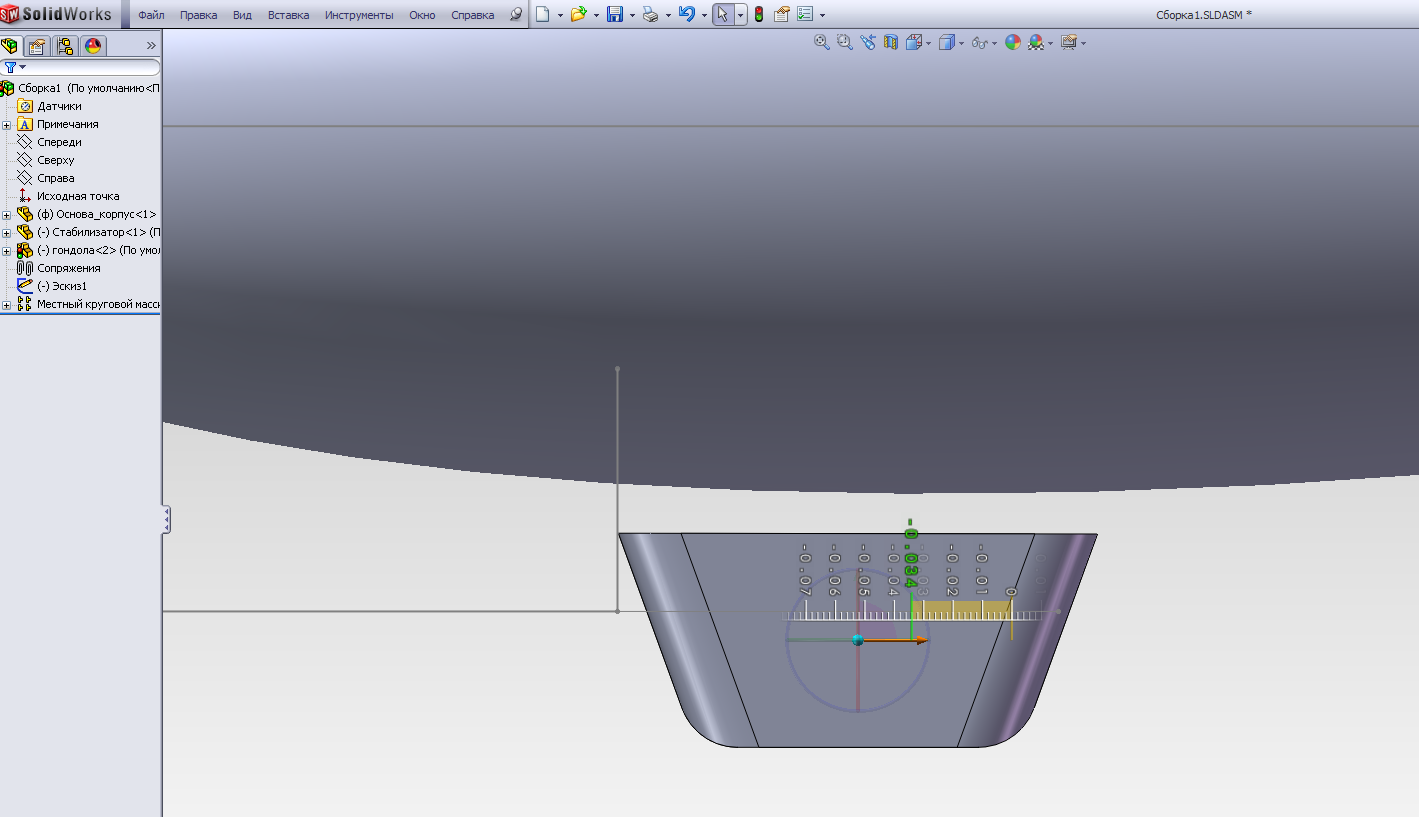
в)
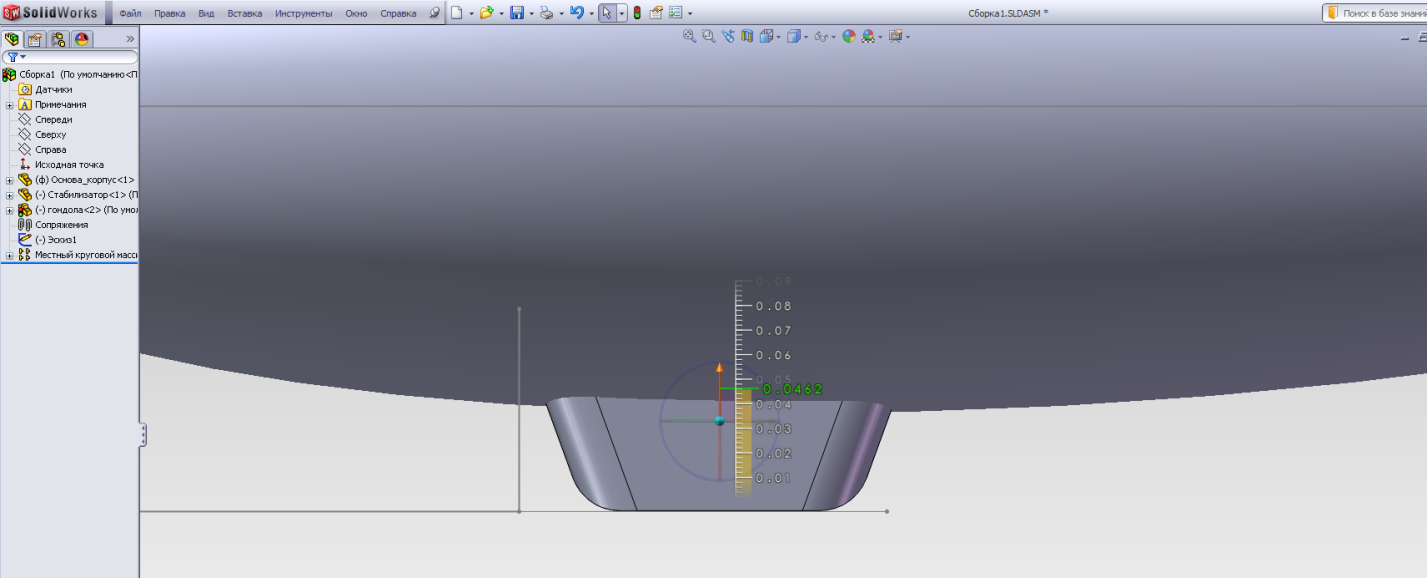
г)
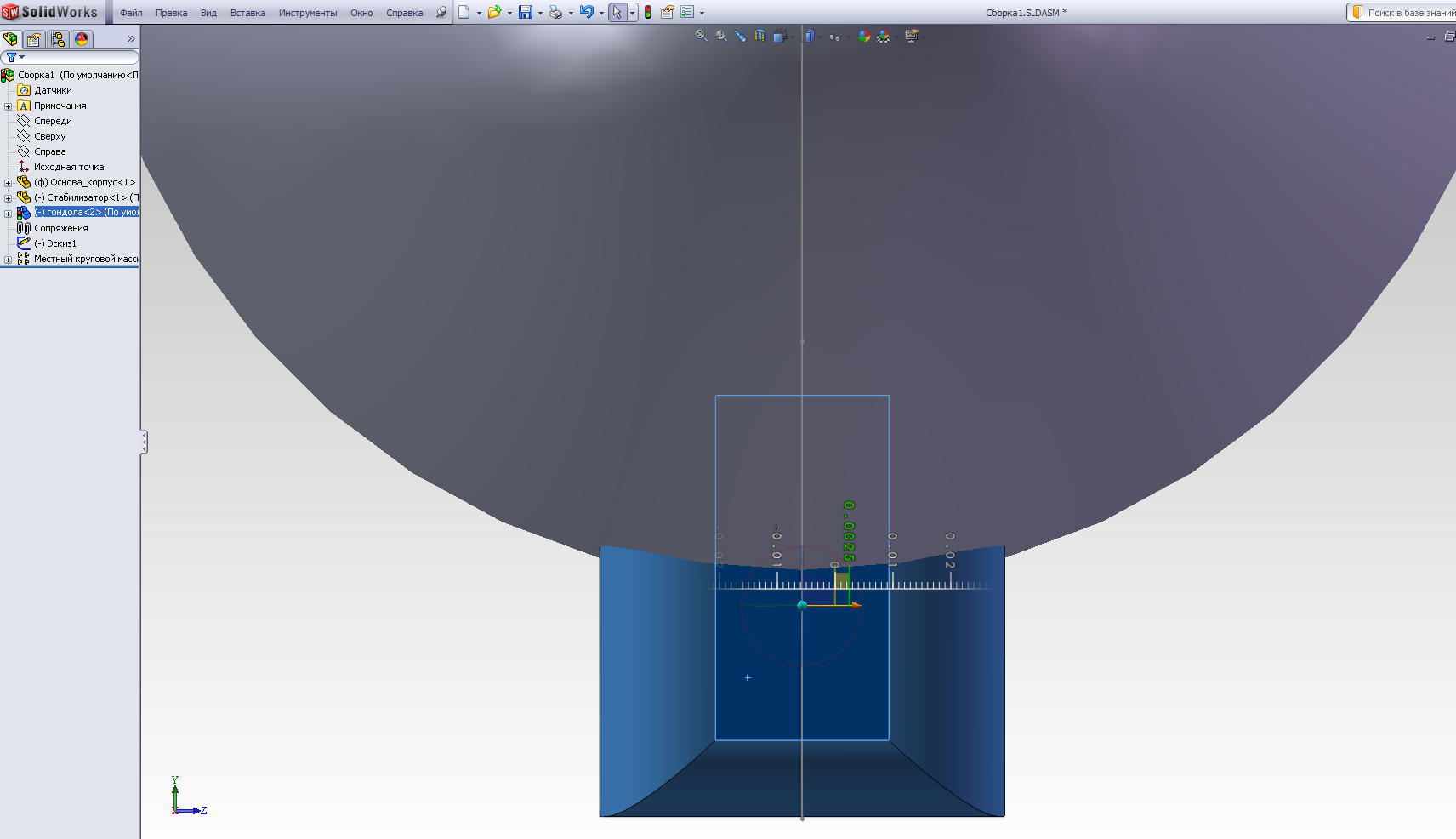
д)
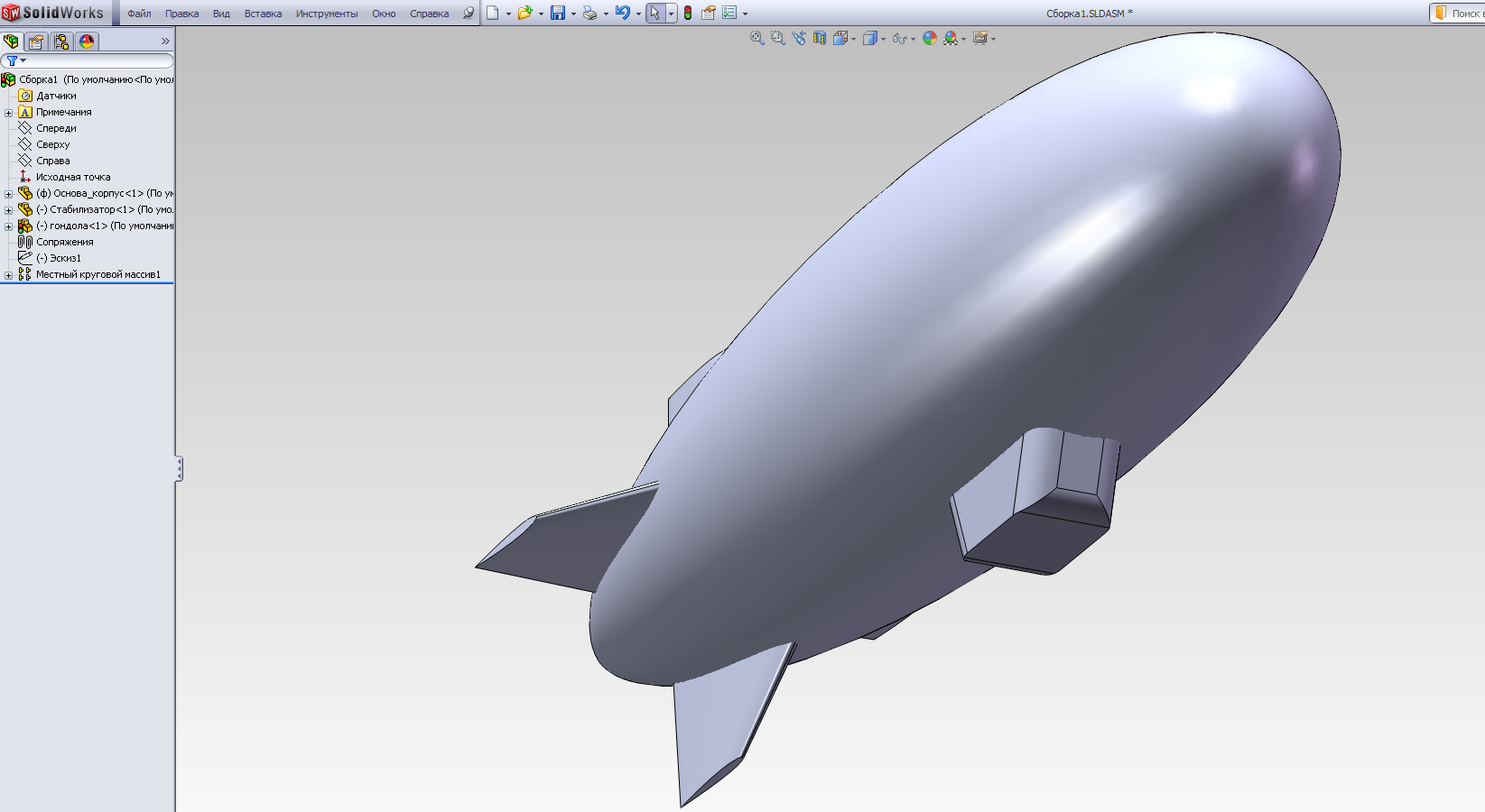
е)
Рис.2.17
Сохраним полученную сборку как деталь с названием Дирижабль, с расширением *sldprt(рис.2.18).
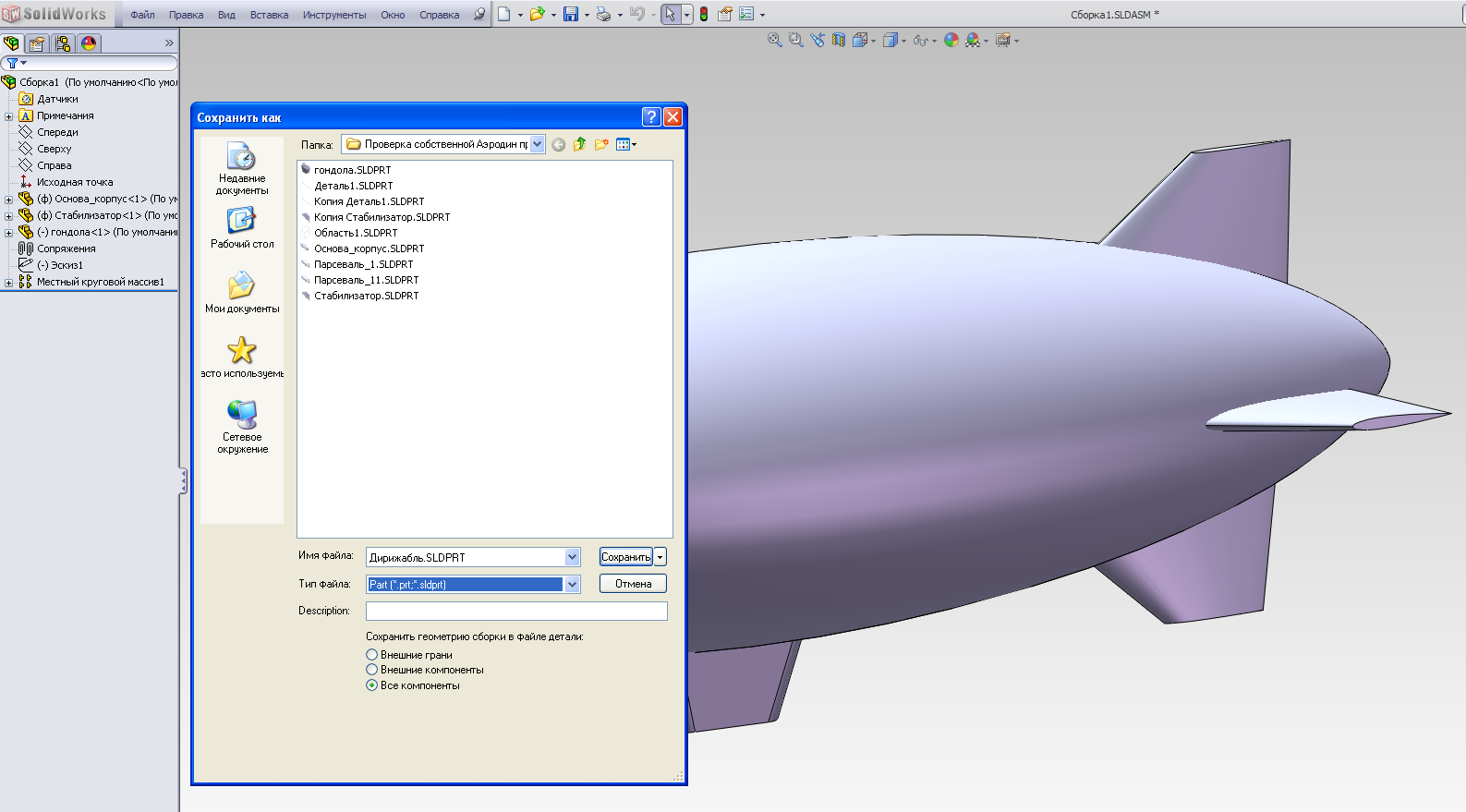
Рис.2.18
Скомбинируем все тела, образующие деталь, с помощью последовательности Вставка – Элементы – Скомбинировать тела (рис.2.19 а). В окне редактирования этой операции с помощью дерева конструирования выбираем в разделе Твердые тела(6) все твердые тела и далее активируем операцию (рис.2.19 б).
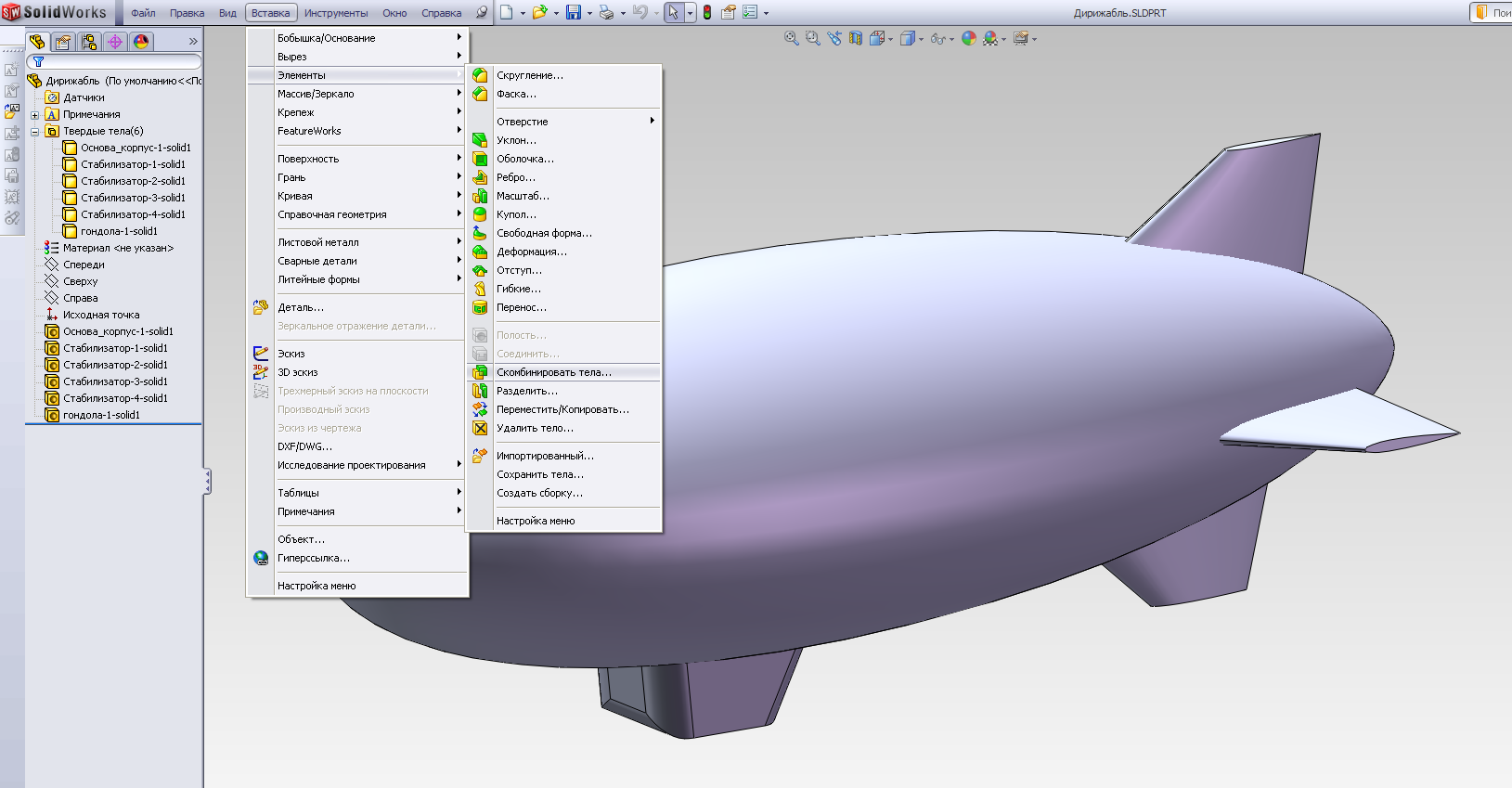
а)
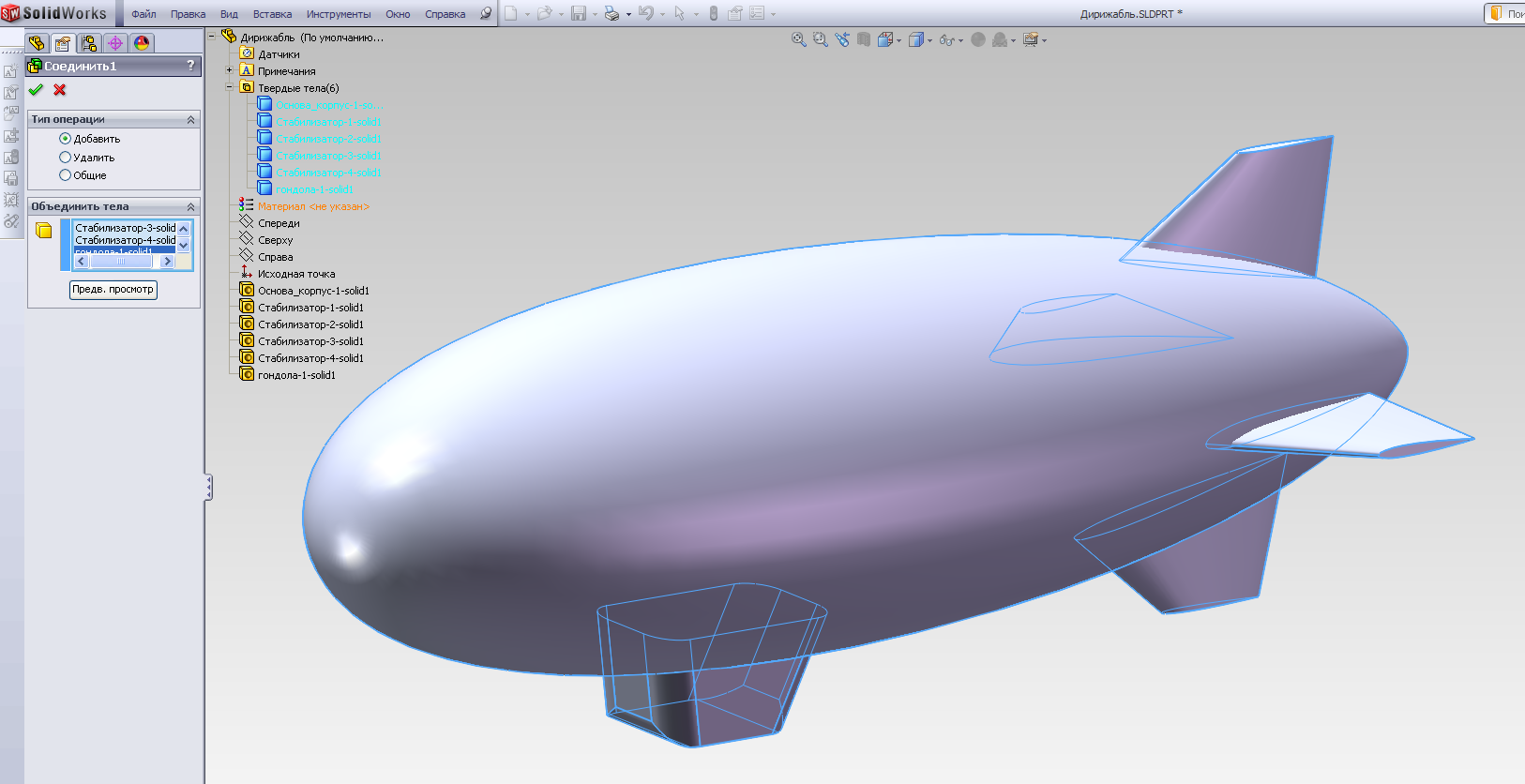
б)
Рис.2.19
Теперь необходимо сшить все грани детали, образовав при этом единое твердое тело. Для этого выполним последовательность Вставка – Поверхность – Сшить поверхность(рис.2.20 а) и в появляющемся окне редактирования выделяем в дереве конструирования все грани твердого тела и далее выбираем опциюПопытаться создать твердотельный элемент(рис.2.20 б). После активации операции в дереве конструирования в разделе твердых тел появляется название Поверхность-Сшить 1.
Далее удалим имеющееся твердое тело Соединить 1 и выполним масштабирование полученного твердого тела – в соответствии с техническим заданием полученная нами трехмерная модель дирижабля является его уменьшенной копией в масштабном соотношении 1:10. Однако для удобства последующего анализа сделаем так, чтобы все размеры в системе были заданы в миллиметрах (потом поясним, для чего), поэтому масштабный коэффициент в соответствующем поле редактирования задаем равным m=10*1000=10000 (рис.2.21 а, б) и активируем операцию масштабирования.
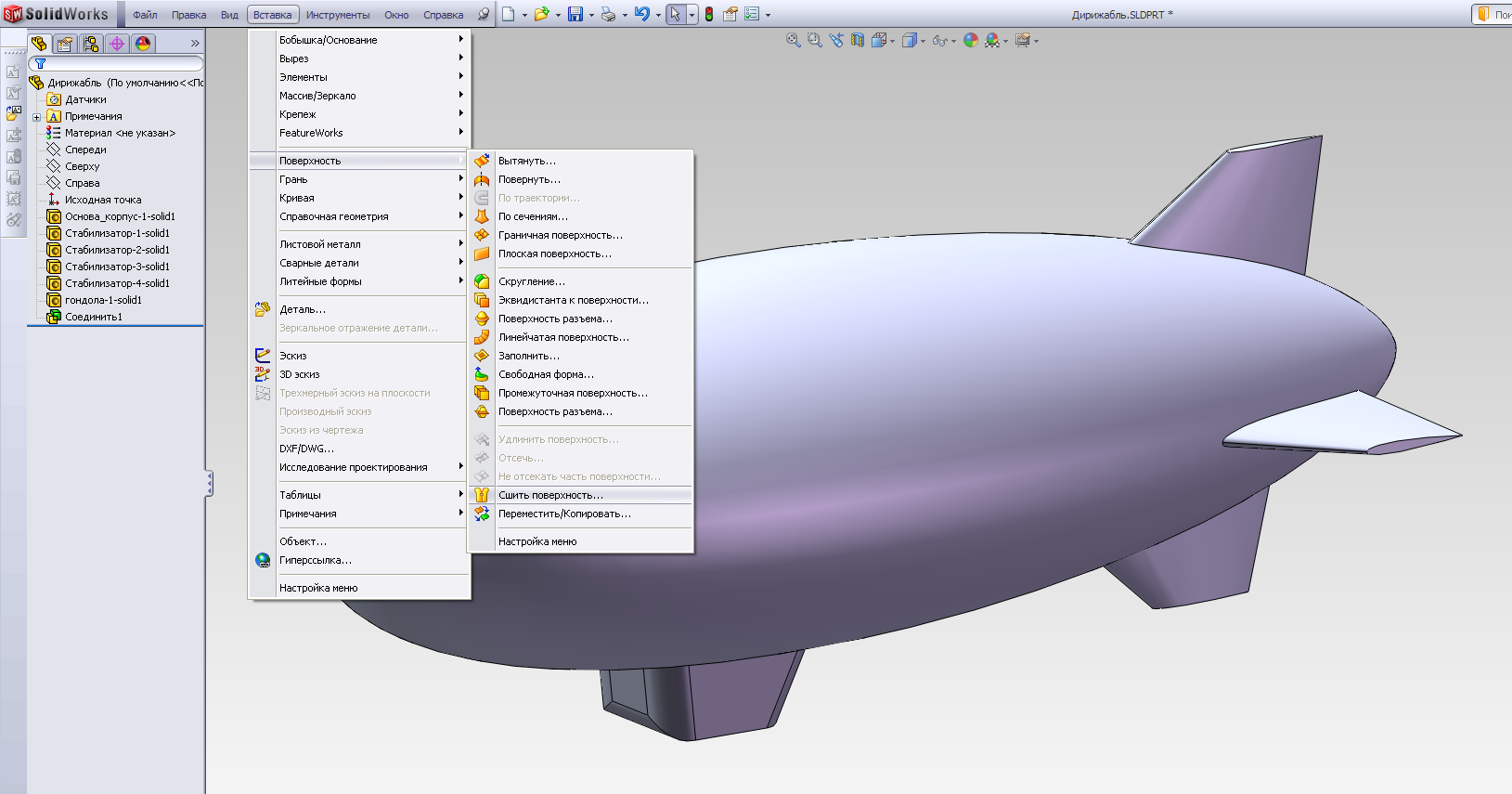
а)
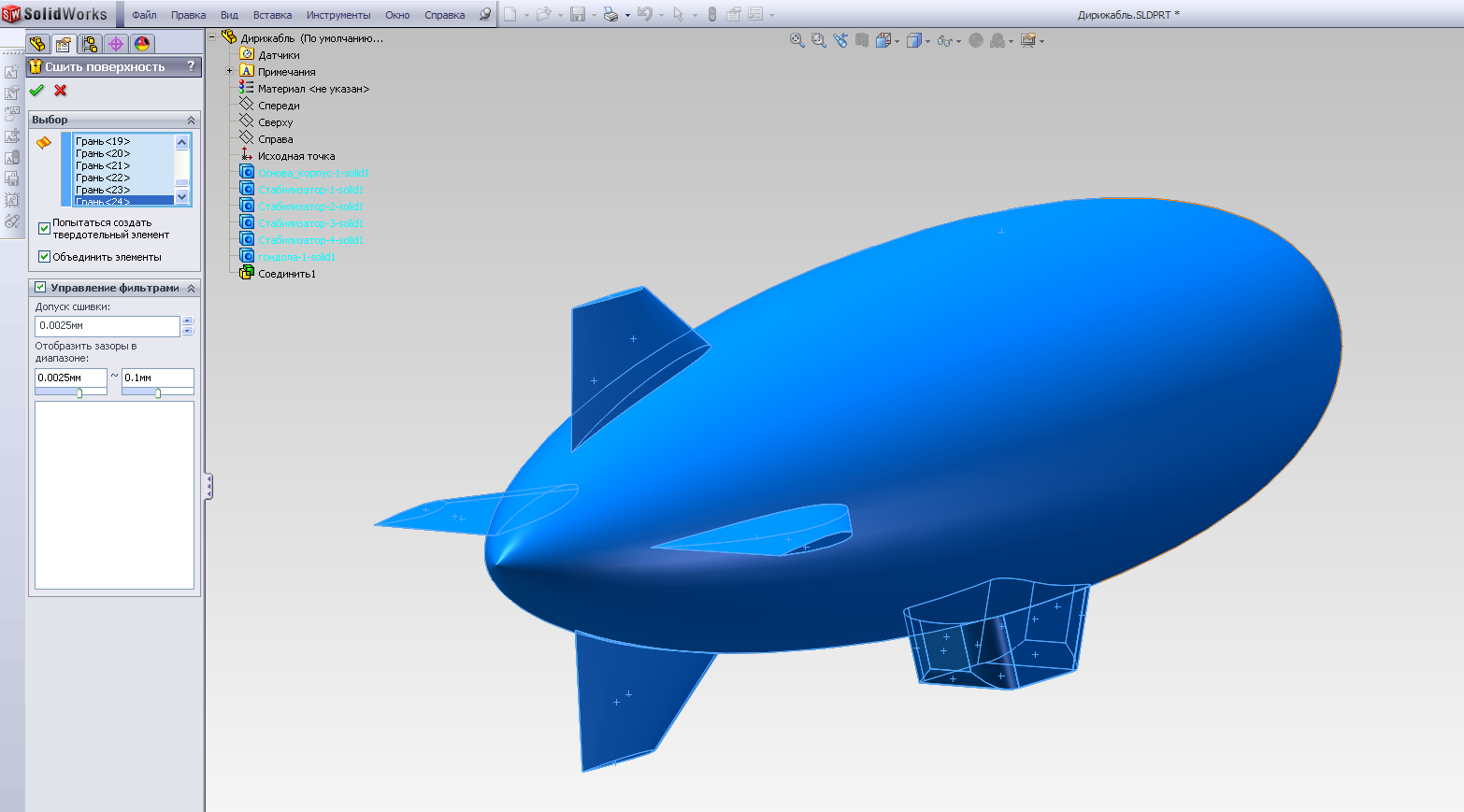
б)
Рис.2.20
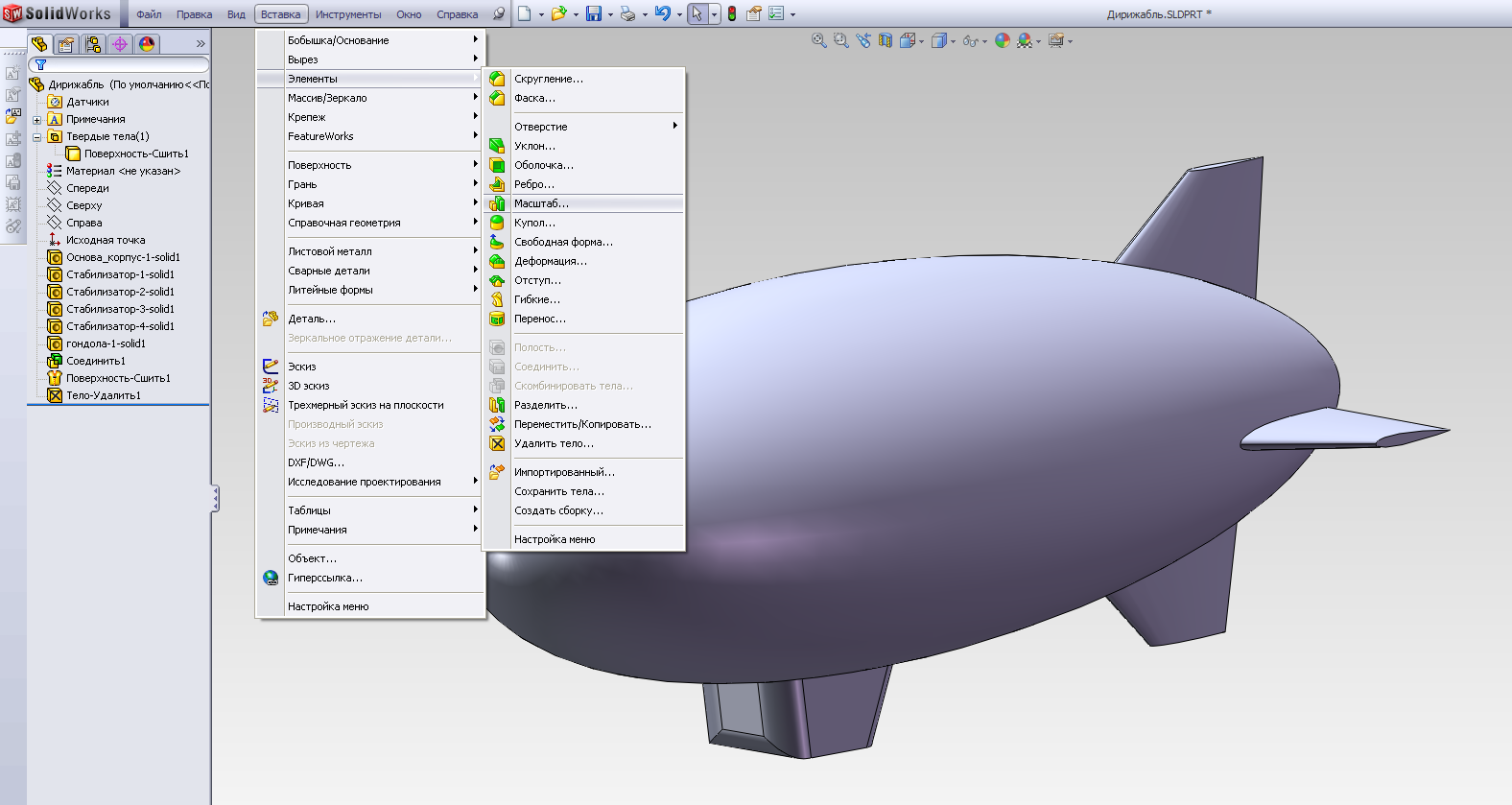
а)
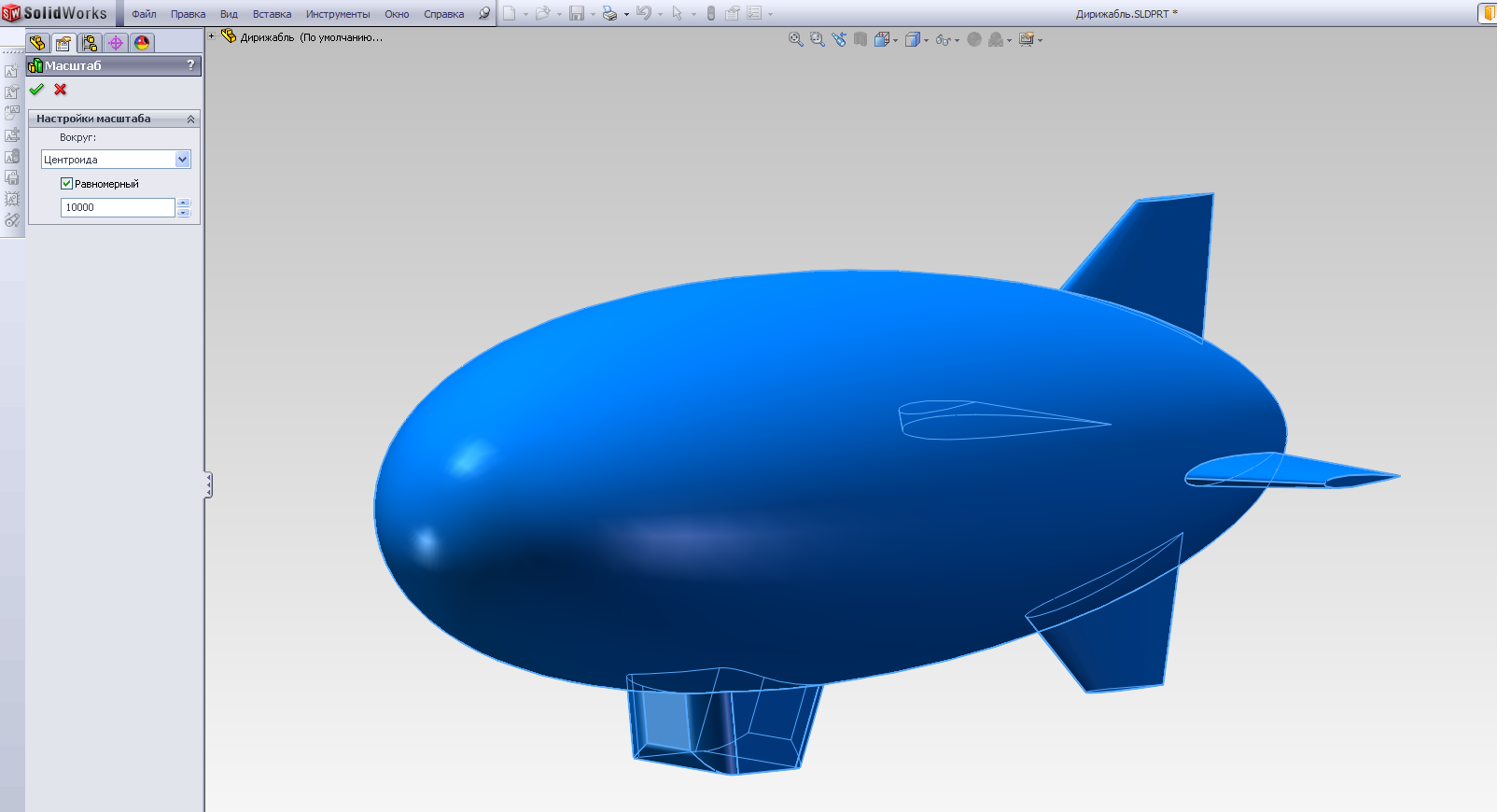
б)
Рис.2.21
Определение массо-инерционных характеристик
Вначале создадим систему координат, относительно которой, согласно ТЗ, будем рассчитывать массо-инерционные характеристики дирижабля. Будем располагать начало этой системы в точке – центре масс тела.
Для нахождения положения центра масс выполняем последовательность: Инструменты – Массовые характеристики. Сворачиваем окно редактирования массовых характеристик и создаем эскиз в продольной плоскости (рис.2.22 а, б), на котором проводим отрезок с правой граничной точкой, совпадающей с точкой центра масс (рис.2.22 в).
Создадим с помощью последовательности Вставка – Справочная геометрия – Система координат систему координат (рис.2.23 а), расположив её начало в центре масс тела (рис.2.23 б), положение которого совпадает с правой граничной точкой построенного отрезка; ось OX ориентируем по направлению продольной оси дирижабля, ось OY – перпендикулярно плоскости симметрии, проходящей через ось OX, ось OZ образует правую тройку с осями OX и OY (рис.2.23 в).
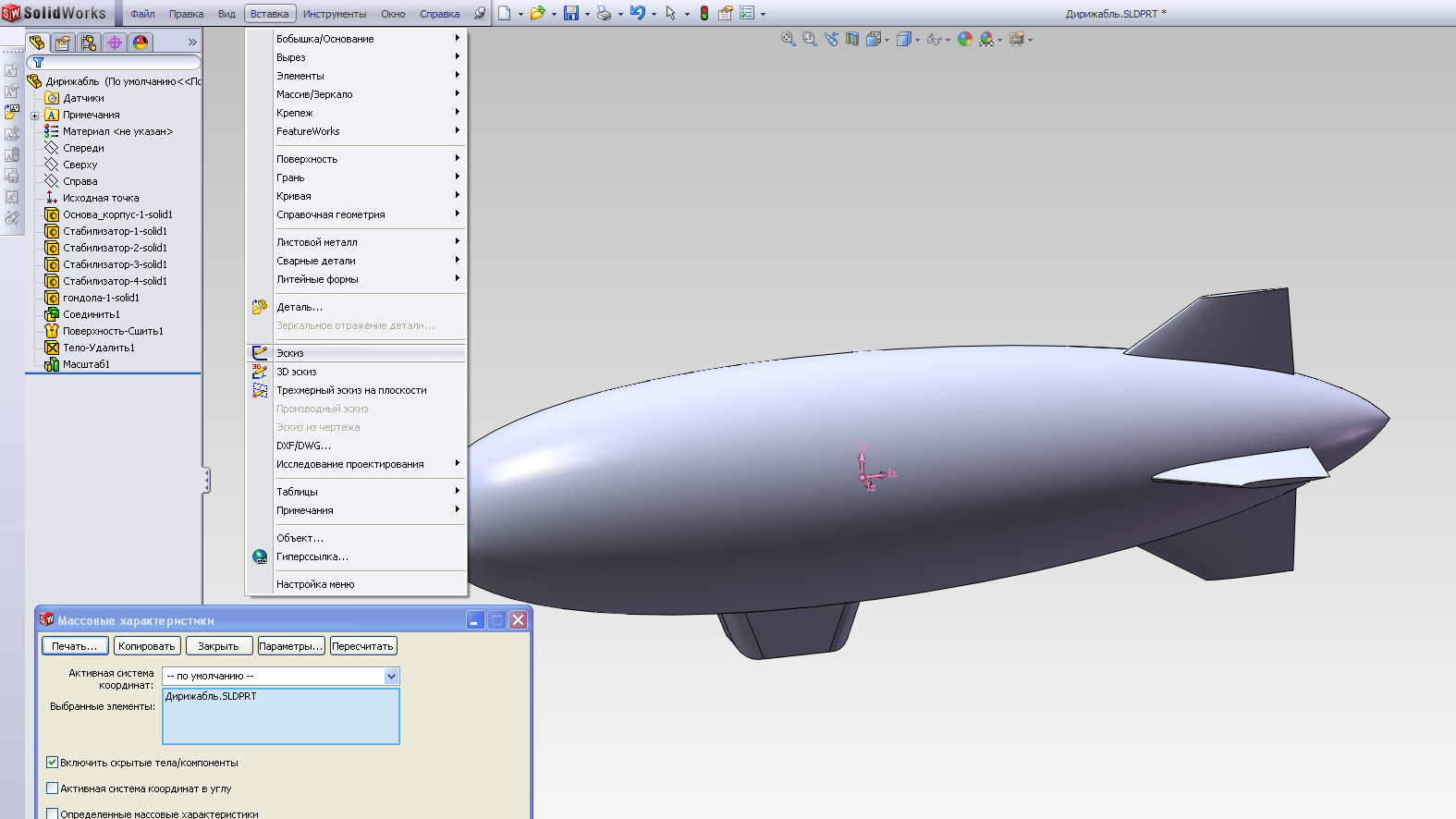
а)
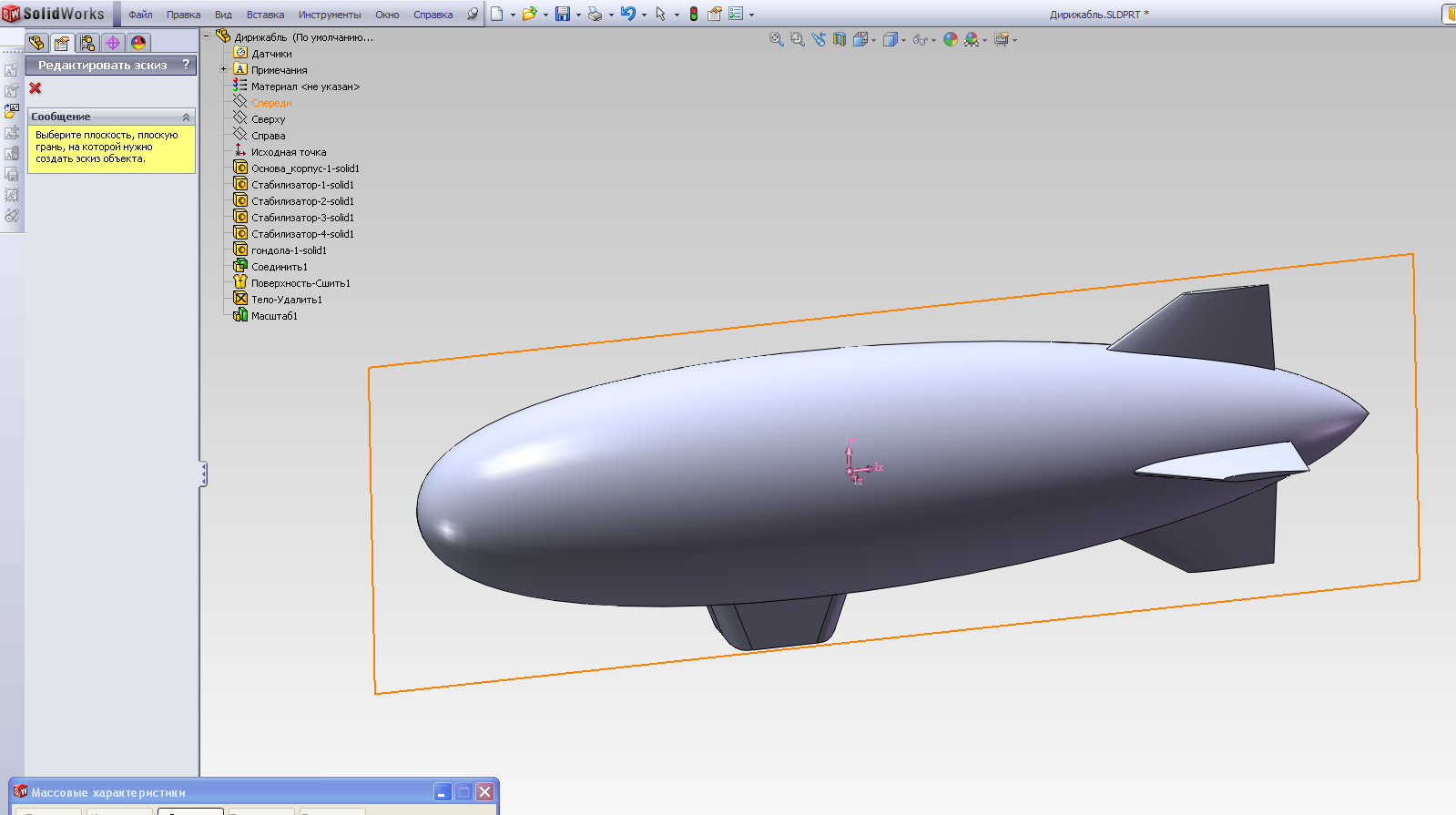
б)
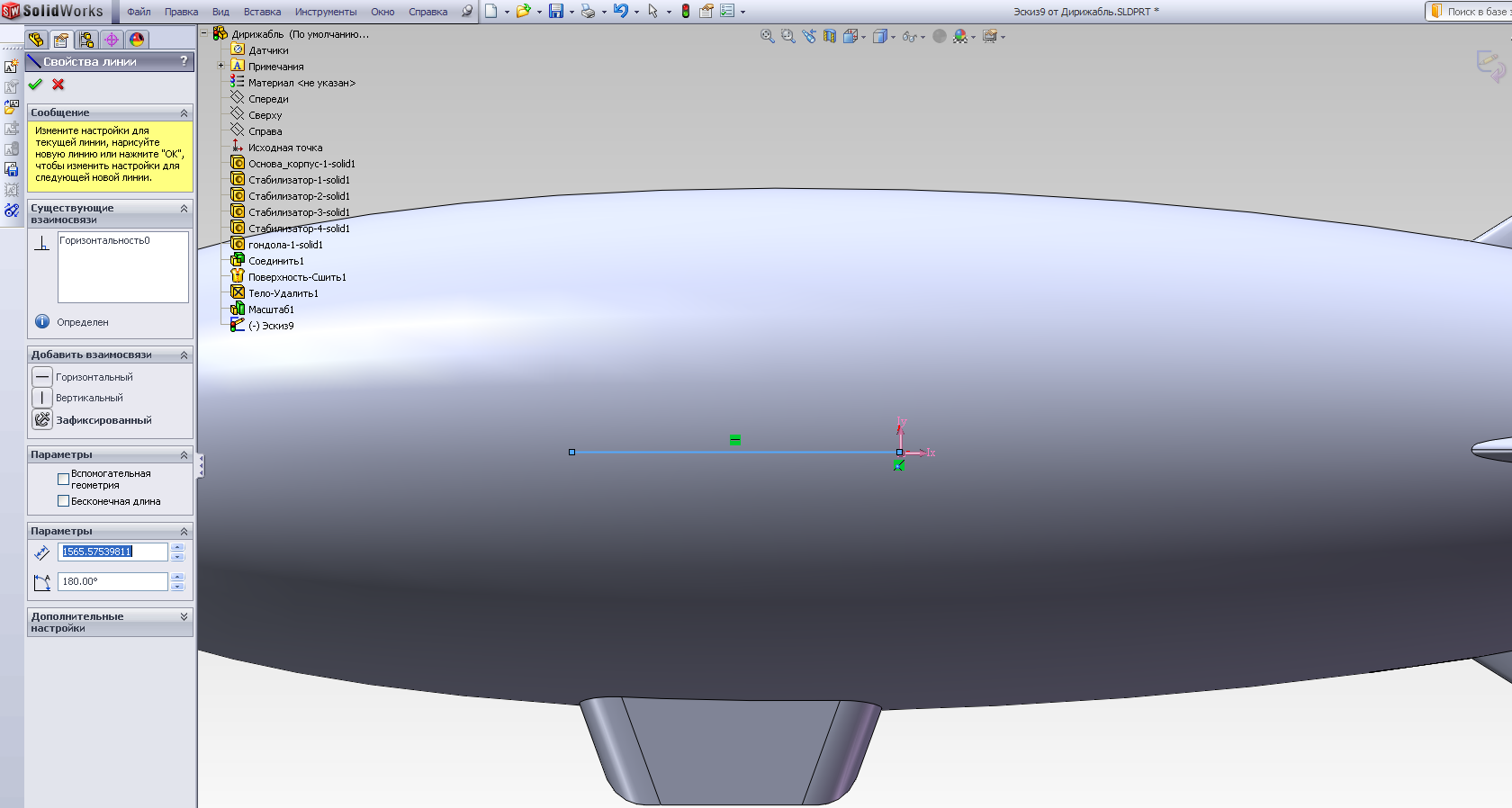
в)
Рис.2.22
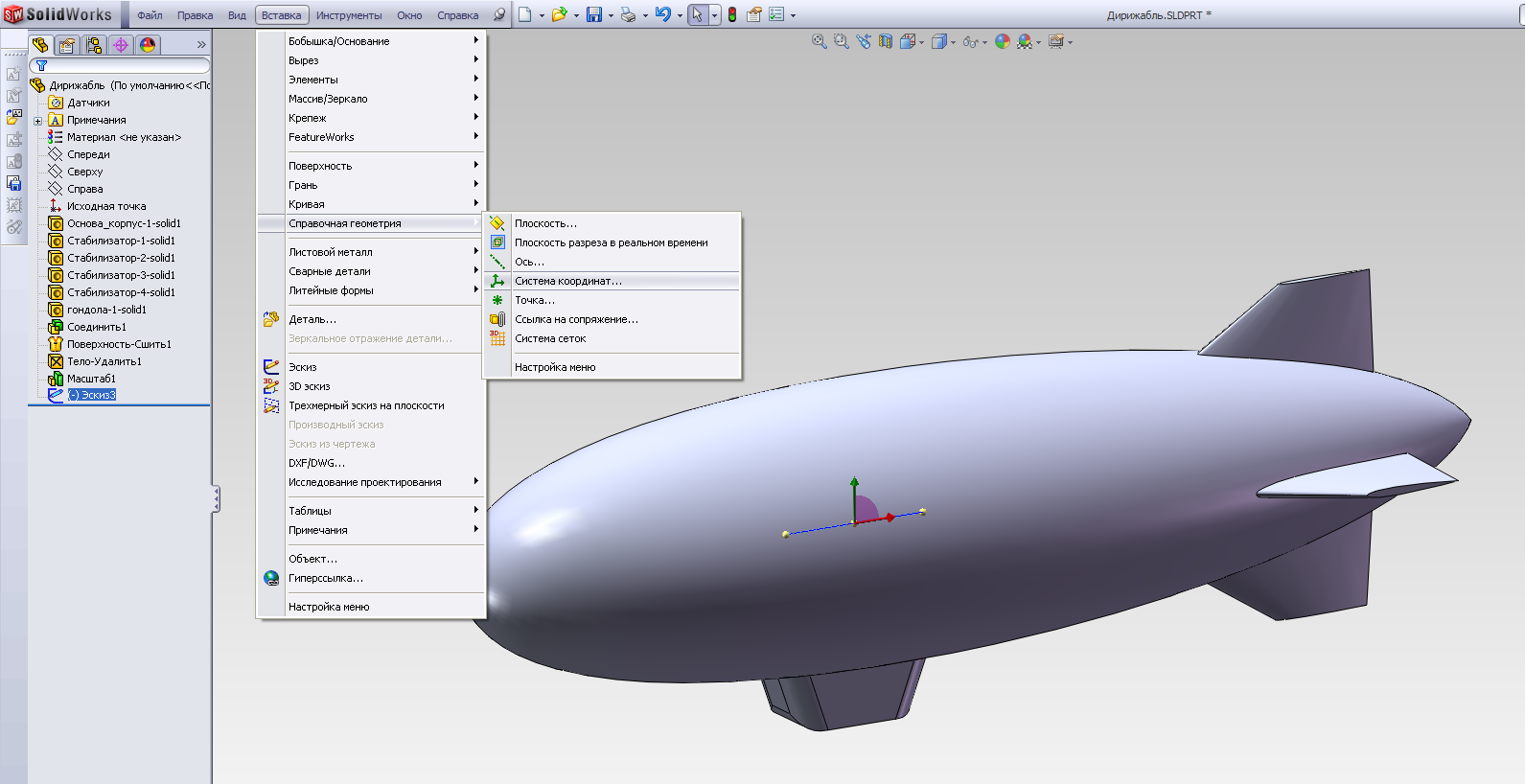
а)
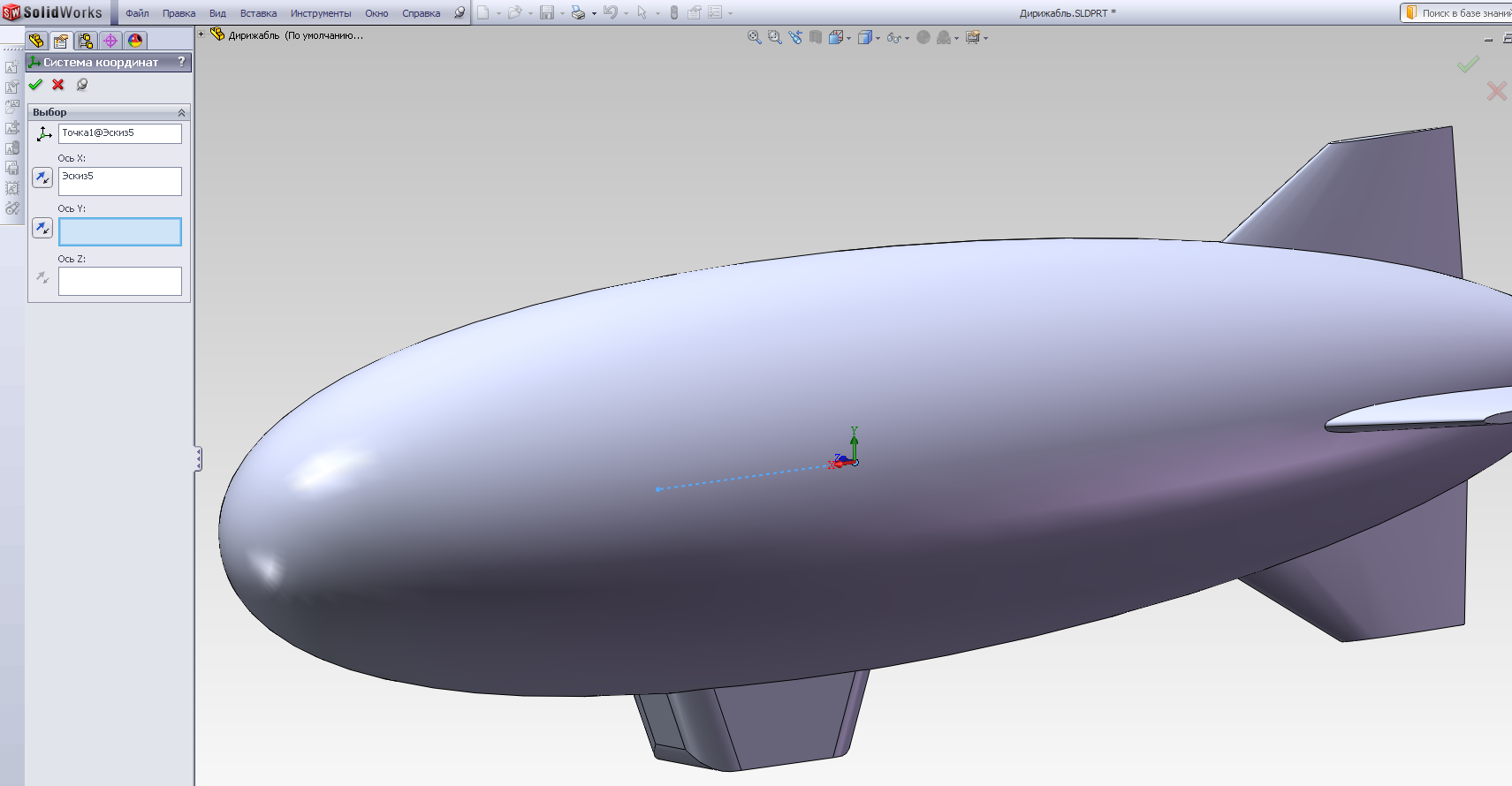
б)
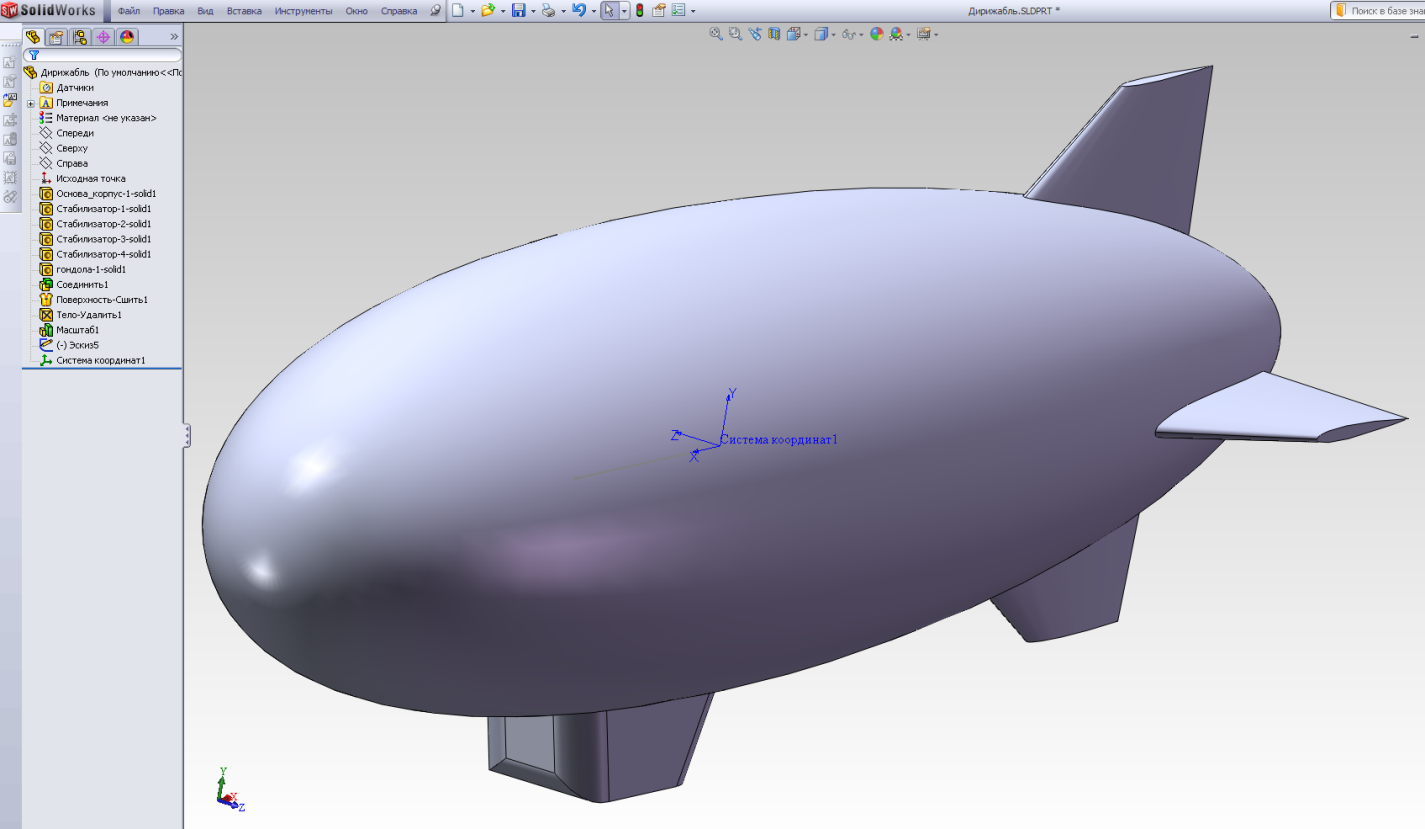
в)
Рис.2.23
Теперь вновь вызываем окно редактирования массо-инерционных характеристик и считываем значение объема тела, равное
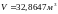(рис.2.24 а). Зная массу дирижабля, равную
,
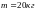находим плотность в приближении
равномерного распределения:
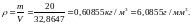
Вызываем вновь окно редактирования массо-инерционных характеристик, в опции Активная система координат выбираем систему Система координат 1; активируем подокно Параметры, выбираем опцию Настройки пользователя, далее - выставляем значения соответствующих параметров так, как показано на рисунке 2.24 б, и активируем вычисления с помощью клавишиПересчитать.
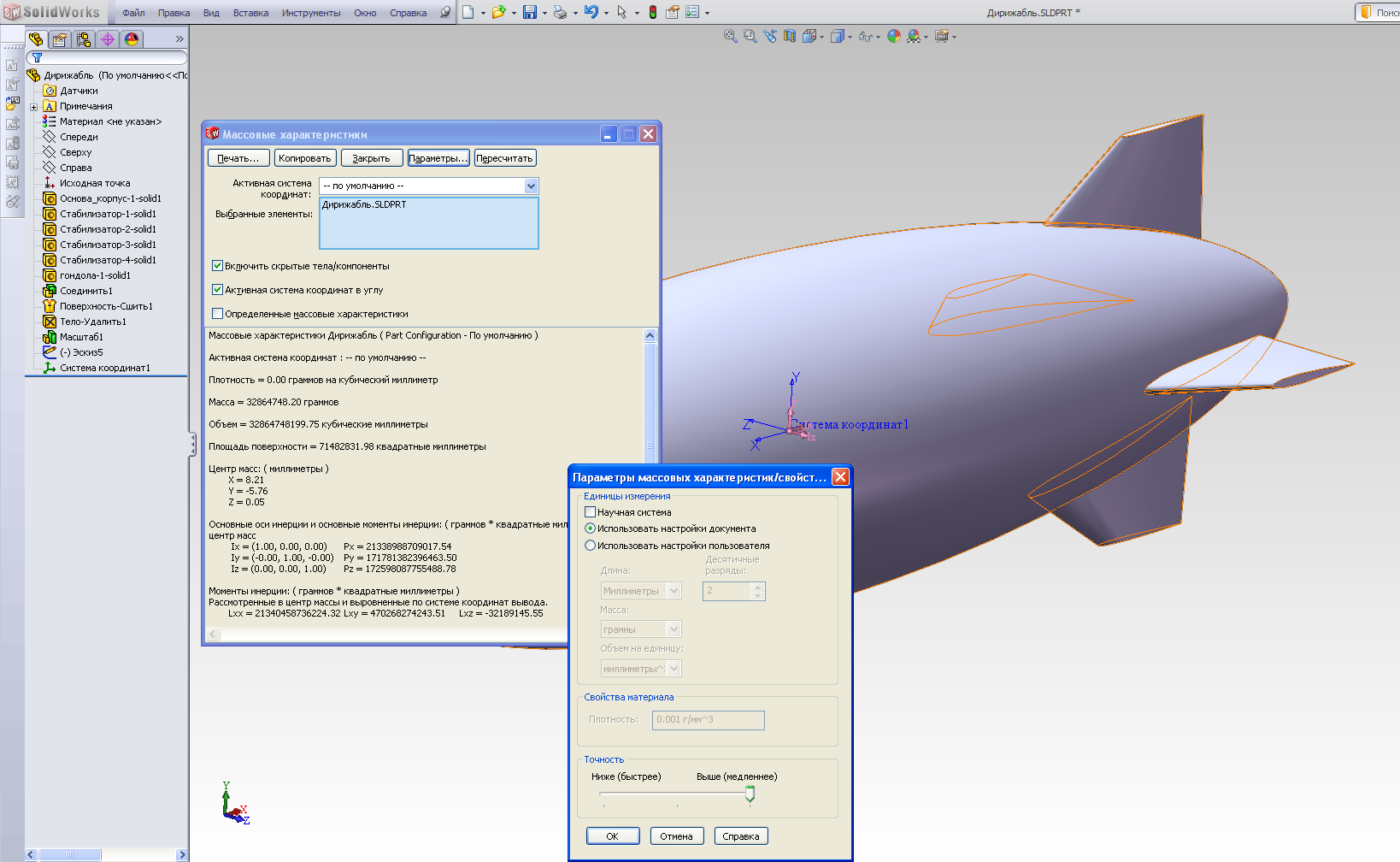
а)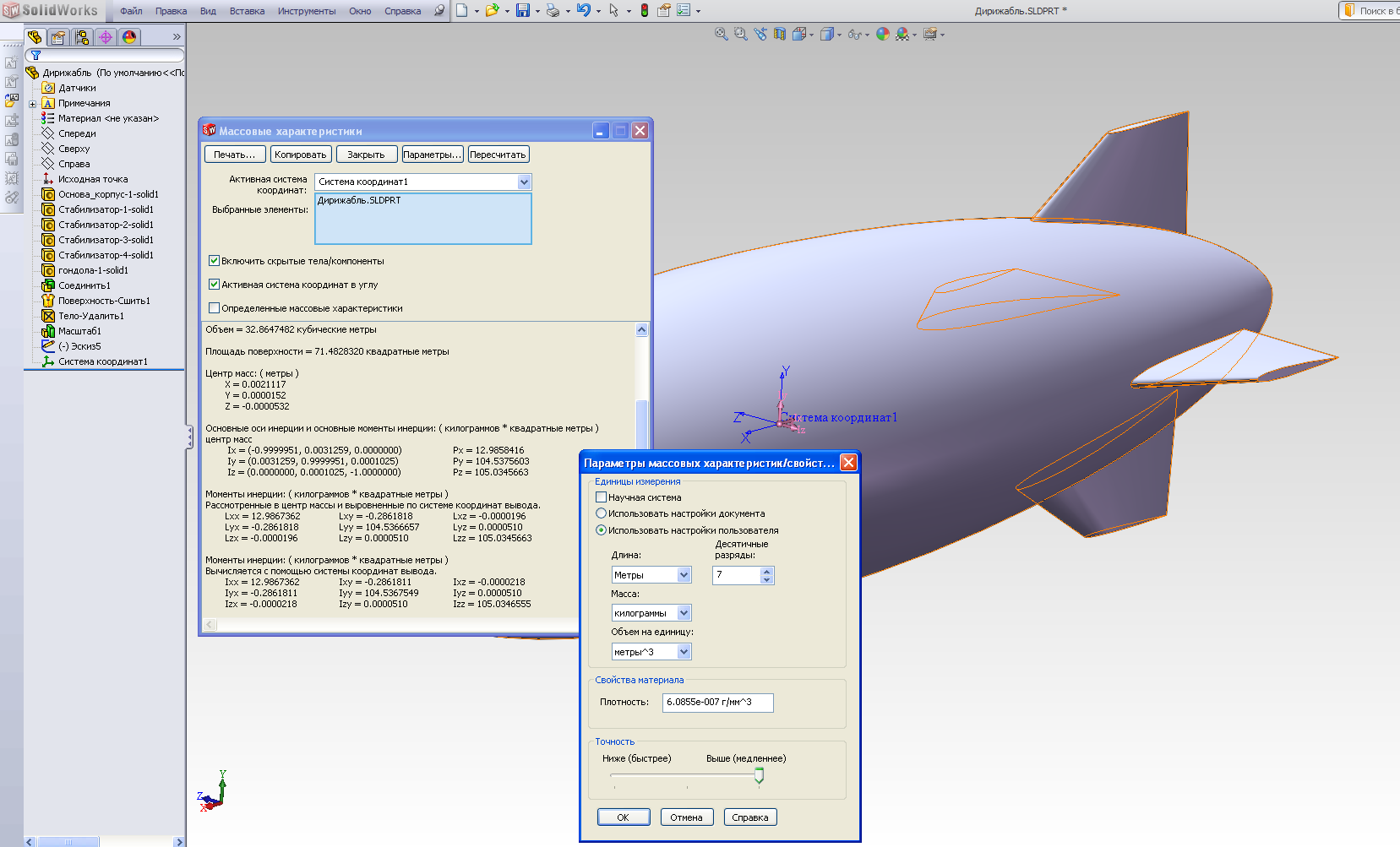
б)
Рис. 2.24
Получившиеся значения массо-инерционных характеристик сведем в таблицу (см. таб.1).
Таблица 1 – Геометрические интегральные и массо-инерционные характеристики дирижабля в приближении равномерного распределения массовой плотности
Геометрические интегральные и массо-инерционные характеристики |
Численные значения |
Масса, m, кг |
20 |
Объем, м^3 |
32,8647 |
Площадь поверхности, м^2 |
71.4828320 м^2 |
Координаты центра масс: |
|
x_c, м |
0 |
y_c, м |
0 |
z_c, м |
0 |
Компоненты тензора инерции: |
|
Jxx, кг*м^2 |
12.9867362 |
Jxy= Jyx, кг*м^2 |
-0.2861811 |
Jxz=Jzx, кг*м^2 |
-0.0000218 |
Jyy, кг*м^2 |
104.5367549 |
Jyz=Jzy, кг*м^2 |
0.0000510 |
Jzz, кг*м^2 |
105.0346555 |
.