3. Построение модели Использование пф в оценке эффективности отрасли

   1. Анализ производительности факторов: средняя и предельная производительность, график переменных, тенденция

На основе расчета предельной и средней производительности капитала мы сможем увидеть, какой выпуск в среднем приходится на 1 единицу ресурса и каков прирост (снижение) выпуска при изменении ресурса на 1 единицу.

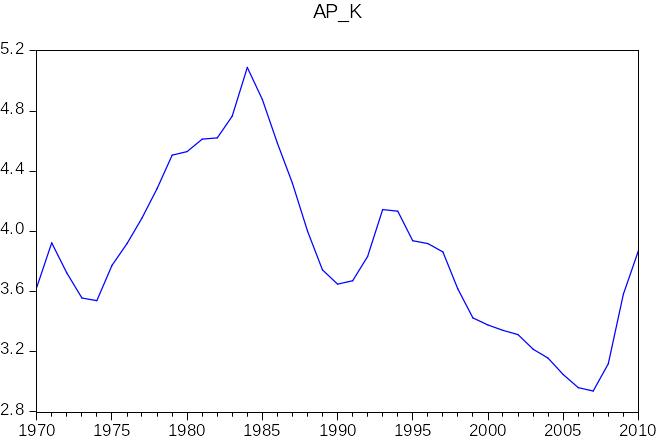
Рис.4 График средней производительности капитала

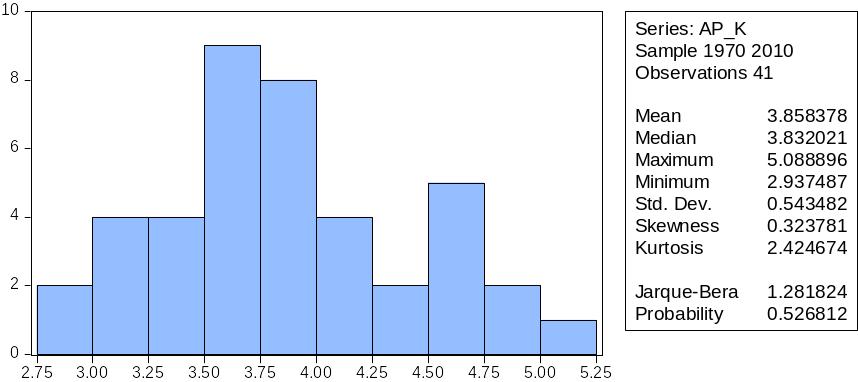
Рис.5 Гистограмма средней производительности капитала, описательные статистики

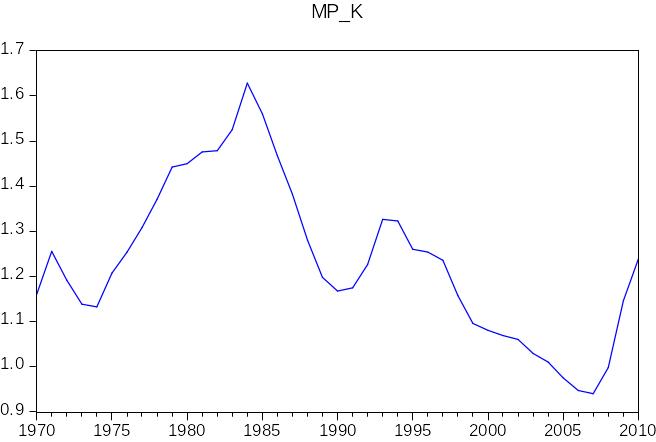
Рис.6 График предельной производительности капитала

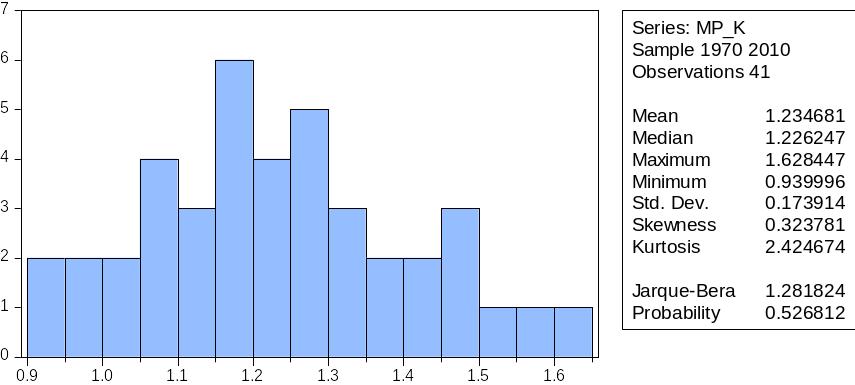
Рис.7 Гистограмма и описательные статистики предельной производительности капитала

Можно отметить тот факт, что графики предельной и средней производительности капитала имеют схожие тенденции. Как видно, пик приходится на 1980-е годы, затем идет скачкообразное развитие.

Предельная и средняя производительность труда показывает несколько иные перспективы. Если пик производительности капитала в рассматриваемый период уже прошел, и нет уверенности, что в прогнозе на будущее значение ее превысит значение 80-х, то производительность труда растет из года в год, и в дальнейшем, скорее всего, будет только повышаться.

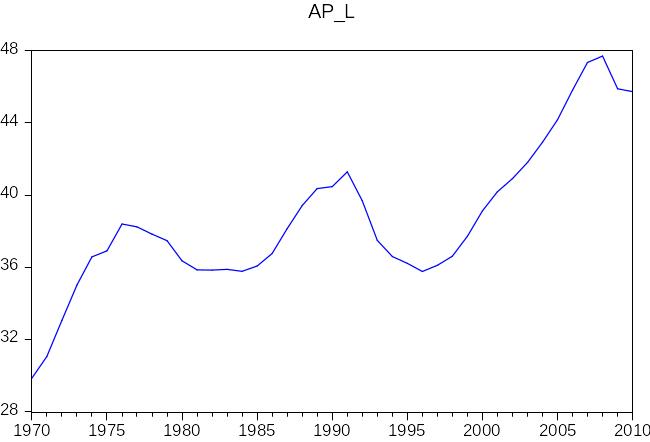
Рис.8 График средней производительности труда

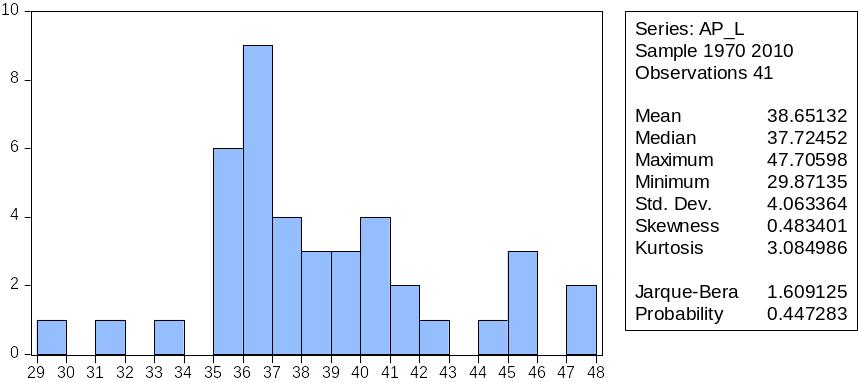
Рис.9 Гистограмма средней производительности капитала, описательные статистики

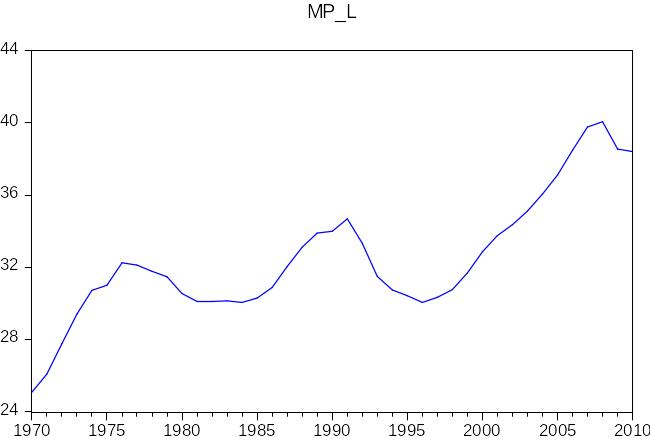
Рис.10 График предельной производительности труда

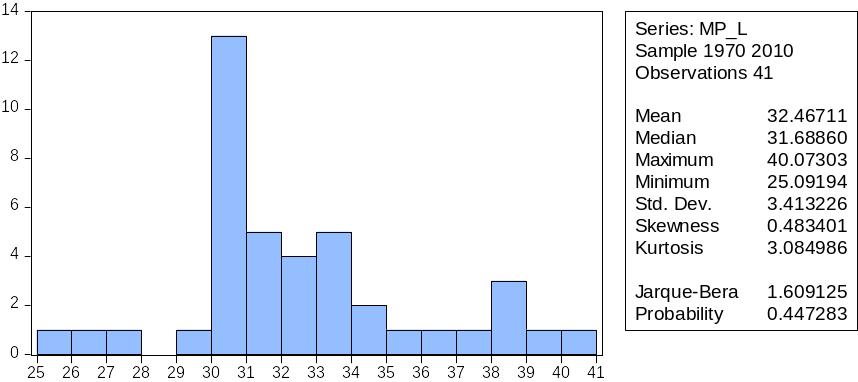
Рис.11 Гистограмма и описательные статистики предельной производительности труда

В сравнении более четко видно, что средняя производительность труда, несмотря на более сильные колебания, имеет тенденцию к повышению, в то время, как средняя производительность капитала практически не изменяет значения, незначительно варьируясь.

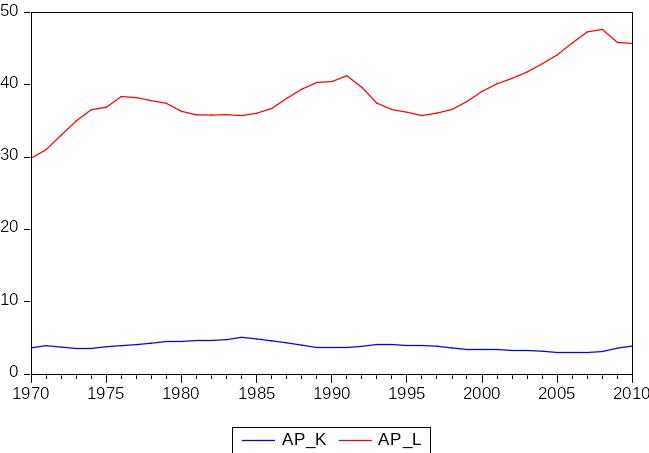
Рис.12 Средняя производительность труда и капитала

2. Анализ эластичности выпуска по факторам и масштабу производства

Эластичность выпуска по факторам производства по каждому периоду приведена в приложении 2. Эластичность выпуска по труду рассчитывается по формуле:

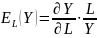
Эластичность выпуска по капиталу – аналогично. Средние значения индексов согласно эмпирическим данным таковы: ε_y^K = 1,08, ε_y^L = 0,71. В функции Кобба-Дугласа коэффициенты a и b соответствуют коэффициентам эластичности выпуска по соответствующим факторам производства (a= 0,32, b=0,84). Мы видим, что эластичность выпуска по труду меньше единицы, но приближается к ней. А эластичность выпуска по капиталу является абсолютной. Можно сказать, что труд является более весомым и редким ресурсом.

Что касается отдачи от масштаба, то это результат воздействия пропорционального изменения обоих факторов:

Этот коэффициент определяет, на сколько изменится выпуск продукции, если объемы использования обоих факторов возрастут на 1%. В данной модели ε_y^λ = 1,16. Данный коэффициент больше единицы, следовательно, объем производства растет быстрее, чем прирост обоих факторов производства. Отдача от масштаба положительная.

Приложение 2. Эластичность выпуска по факторам производства (L и K)

εyL	εyK
0,56	-0,61
1,61	0,67
1,88	0,59
2,08	0,54
2,37	0,49
1,07	1,50
0,86	12,45
0,56	-0,60
-1,06	0,17
0,87	8,84
-1,80	0,22
1,22	1,03
0,41	-0,30
-0,62	0,13
3,43	0,43
3,11	0,45
2,61	0,48
3,18	0,45
3,23	0,44
1,61	0,67
-0,11	0,04
0,50	-0,45
-0,78	0,15
0,93	3,42
1,33	0,86
1,08	1,43
0,50	-0,49
0,24	-0,13
-1,92	0,23
-15,05	0,31
1,71	0,63
1,84	0,59
1,61	0,67
2,94	0,45
-0,50	0,12
0,28	-0,17
0,56	-0,66
0,88	7,25
3,69	0,39
1,65	0,65

Приложение 1. Исходные данные модели: добывающая промышленность экономики Испании.

	добывающая промышленность		Y	L	K
1970			9044,492	302,7815	2492,963
1971			9600,723	309,1351	2447,126
1972			11012,42	333,0597	2957,869
1973			12186,42	347,9765	3426,212
1974			12942,94	353,7901	3657,821
1975			12866,93	348,5526	3410,419
1976			13309,74	346,6038	3396,871
1977			13929,91	364,1844	3408,301
1978			14207,45	375,4685	3316,24
1979			14194,15	378,7614	3149,552
1980			14322,01	393,8479	3161,514
1981			14170,95	395,2165	3072,533
1982			14011,63	390,8475	3032,268
1983			14205,56	395,836	2980,906
1984			14338,99	400,7581	2817,702
1985			14562,63	403,6262	2986,814
1986			15030,93	408,849	3277,395
1987			15924,75	417,4371	3687,224
1988			16736,9	424,5021	4182,839
1989			17369,49	430,3235	4640,186
1990			17763	438,9128	4868,141
1991			18060,46	437,3602	4919,473
1992			18064,7	455,1236	4714,144
1993			17454,43	465,5001	4211,108
1994			17546,76	479,4448	4244,511
1995			18548,98	511,9989	4710,859
1996			18889,03	527,9649	4820,806
1997			18848,39	521,8079	4880,204
1998			18589,78	507,6133	5139,19
1999			18983,48	503,2133	5543,426
2000			19671,76	502,714	5825,73
2001			20637,12	513,4612	6176,985
2002			21265,21	519,7384	6418,465
2003			22517,08	538,558	7002,631
2004			23305,23	542,8701	7383,357
2005			23691,74	536,2368	7774,485
2006			23993,75	523,5629	8105,329
2007			24261,36	512,3662	8259,223
2008			25939,9	543,7453	8317,542
2009			24379,2	531,1403	6805,85
2010			22968,82	502,1798	5931,008