Лабораторная работа №1 по дисциплине «Моделирование рыночной экономики» по теме: «Оценка эффективности отрасли на основе производственной функции», вариант 12

Выполнил:

студентка гр. ЭТ-91

Шорохова И.П.

Проверил:

преподаватель кафедры ММЭ

Захарченко Н.Г.

Цель: анализ эффективности отрасли на основе производственной функции

План работы:

1. Характеристика статистической информации, анализ матрицы коэффициентов корреляции

   1. Характеристики центра тяжести распределения X_ср , мода, медиана

   2. Характеристика разброса индивидуального значения вокруг среднего, дисперсия, среднее квадратическое отклонение, коэффициент вариации

   3. Характеристика формы распределения, асимметрия, эксцесс

2. Оценка производственной функции (ПФ) для конкретной отрасли

   1. Спецификация модели: выбор факторных переменных и формы модели

   2. Верификация модели: оценка ее адекватности

3. Построение модели Использование ПФ в оценке эффективности отрасли

   1. Анализ производительности факторов: средняя и предельная производительность, график переменных, тенденция

   2. Анализ эластичности выпуска по факторам и масштабу производства

   3. Построение и анализ изоквант

1. Характеристика статистической информации, анализ матрицы коэффициентов корреляции

1. Характеристики центра тяжести распределения Xср , мода, медиана

Исходная информация представлена для статистических данных добывающей промышленности Испании (см. Приложение 1). Перейдем к характеристике имеющейся статистической информации.

	Y	L	K
Mean	17301.20	442.3676	4672.079
Median	17454.43	437.3602	4244.511
Maximum	25939.90	543.7453	8317.542
Minimum	9044.492	302.7815	2447.126
Std. Dev.	4301.566	73.82636	1722.568
Skewness	0.207004	-0.167948	0.727396
Kurtosis	2.235914	1.709679	2.400903
Jarque-Bera	1.290184	3.036995	4.228698
Probability	0.524614	0.219041	0.120712
Sum	709349.2	18137.07	191555.2
Sum Sq. Dev.	7.40E+08	218013.3	1.19E+08
Observations	41	41	41

Табл. 1 Описательные статистики

Как видим, здесь вычислены следующие характеристики анализируемых переменных: средняя арифметическая (Mean), медиана, максимальное и минимальное значения, стандартное отклонение (Std. Dev.), асимметрия (Skewness) и эксцесс (Kurtosis). Кроме того, вычислена статистика Харке–Бера (Jarque–Bera) и вероятность, что её значение не превышает критического значения. Ниже указаны сумма всех элементов выборки, сумма квадратов отклонений (Sum. Sq. Dev.), и число обработанных наблюдений.

1.2 Характеристика разброса индивидуального значения вокруг среднего, дисперсия, среднее квадратическое отклонение, коэффициент вариации

Используя описательные статистики (см. табл. 1) несложно посчитать размах вариации (как разность между максимальным и минимальным значениями), мы видим и отклонение (Std. Dev.). Для наглядности представим это на графике:

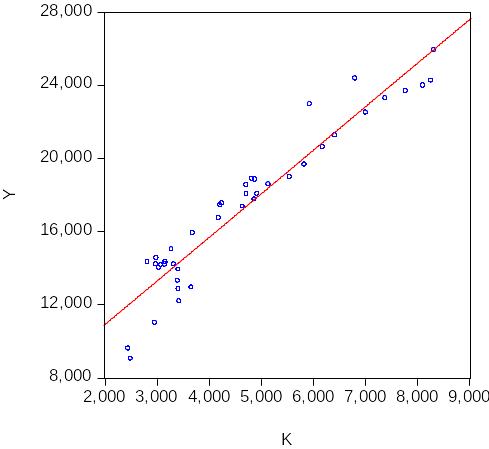
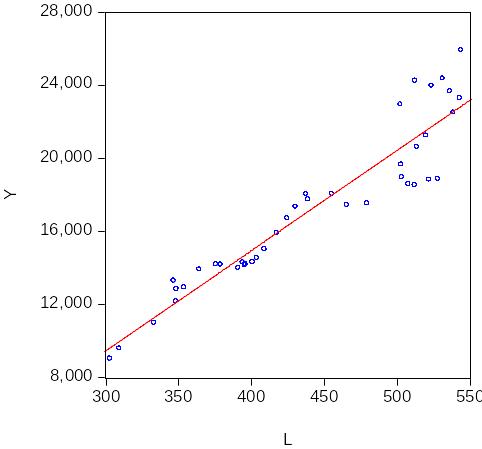
Рис.1 График scatter regression для L и K(диаграмма рассеяния с наложенной линией регрессии)

Рассчитаем так же дисперсию и среднее квадратическое отклонение по формулам:

D = ∑(x_i-x_ср)² / n

σ = D^1/2

	Y	L	K
дисперсия	18052169,72	284225538,65	2894870,01
сркв откл	4248,78	16858,99	1701,43

Табл. 2 Дисперсия и среднее квадратическое отклонение