
шпоры вышмат
.docx1.Определенный интеграл и его свойства.


2. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
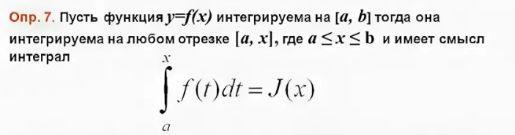

3.
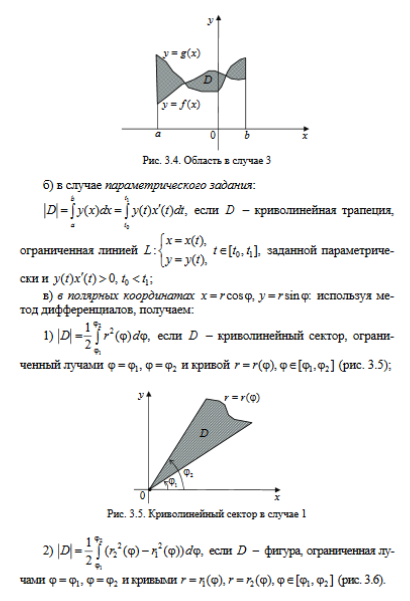
Применение определенного интеграла к
вычислению площадей, длин, дуг, объемов
тел

![]()
![]()

![]()


4. Несобственные интегралы и признаки их сходимости.
![]()


5. Основные понятия теории дифференциальных уравнений
![]()
6. Дифференциальные уравнения 1-го порядка, теорема существования и единственности решения задачи Коши.


7. Основные классы дифференциальных уравнений 1-го порядка, интегрируемых в квадратурах: с разделяющимися переменными, однородные, линейные, Бернулли.
![]()



8. Дифференциальные уравнения высших порядков: основные понятия.

9.
Дифференциальные уравнения 2-го порядка,
допускающие понижение порядка.

10. : фундаментальная система решений, структура общего решения однородного и неоднородного линейных дифференциальных уравнений.





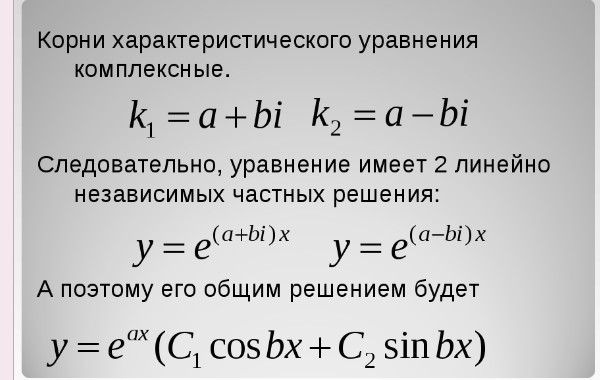
11. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами: структура общего решения, специальная правая часть, метод подбора частных решений, метод Лагранжа вариации произвольных постоянных.




12. Общее понятие о системах дифференциальных уравнений*, задача Коши.


13. Нормальные системы дифференциальных уравнений.



14. Линейные системы дифференциальных уравнений с двумя неизвестными функциями и их решение методом сведения к дифференциальному уравнению относительно одной неизвестной функции.
![]()

15. Преобразование Лапласа: определения и свойства.

![]()
![]()
![]()

16. Решение линейных дифференциальных уравнений с постоянными коэффициентами и их систем с помощью преобразования Лапласа.

17. Двойной интеграл и его свойства.
Двойным интегралом функции f(x,y – вместо М) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном увеличении числа разбиений n
![]()


18. Вычисление двойного интеграла повторным интегрированием в декартовых и полярных координатах.
19. Тройной интеграл, его свойства.
20. Вычисление тройных интегралов повторным интегрированием в декартовых и цилиндрических координатах.
21. Криволинейные интегралы первого и второго рода, их свойства и вычисление.
22. Понятие о поверхностных интегралах первого и второго рода, их свойства и вычисление.
23. Скалярные и векторные поля.

24. Основные характеристики векторного поля: циркуляция, ротор, поток, дивергенция.
![]()



Поток
![]()


25. Теоремы Остроградского, Стокса и Грина.



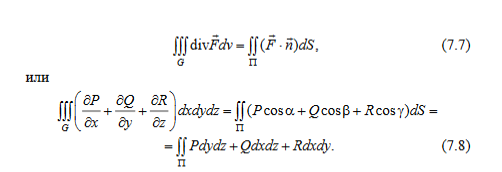


26. Потенциальные и соленоидальные поля

