Действия над линейными операторами.

Определение. Произведением (композицией) линейного оператора f на линейный оператор g называется оператор, являющийся последовательным применением операторов f и g, обозначается , т. е. для вектора x имеем .

Произведение линейных операторов само является линейным оператором. Действительно, для любых векторов и исходя из определения линейного оператора имеем: .

Теорема. Если в некотором базисе линейные операторы f и g имеют соответственно матрицы А и В, то их произведение имеет матрицу ВА.

Определение. Сумма линейных операторов f и g некоторого линейного пространства – это такой оператор h, что для любого вектора x выполняется равенство . Обозначается .

Справедливо . Сумма линейных операторов является линейным оператором.

Теорема. Если линейные операторы f и g в некотором базисе имеют соответственно матрицы А и В, то их сумма в том же базисе имеет матрицу В+А.

Линейные операторы могут быть вырожденными (имеют вырожденную матрицу) и невырожденные.

Теорема. Произведение двух линейных невырожденных операторов есть невырожденный линейный оператор.

□ Если А и В матрицы операторов f и g, то матрица произведения операторов равна ВА, ее определитель равен , поскольку и .■

Ортогональные матрицы.

Пусть имеется евклидово n-мерное пространство .

Определение. Матрица ортонормированной системы векторов называется ортогональной. Для таких ортонормированных векторов имеем

Единичные матрицы ортогональны. Например, ортогональными являются следующие единичные матрицы:

.

Теорема. Для того чтобы матрица А была ортогональной, необходимо и достаточно, чтобы выполнялось равенство .

□ Если обозначить , то элементы этой матрицы будут равны

элементы транспонированной матрицы. Но это означает, что или . И обратно, если , имеем равенство

Что означает ортогональность матрицы А. ■

Следствия.

1. Модуль определителя ортогональной матрицы равен1.

2. Ортогональная матрица – невырожденная.

3. Произведение двух ортогональных матриц – ортогональная матрица.

4. Необходимым и достаточным условием ортогональности матрицы А является .

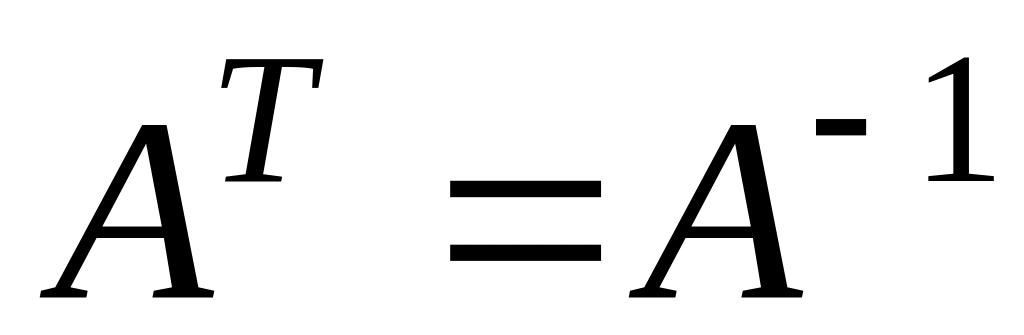5. При транспонировании ортогональной матрицы получается ортогональная матрица.

6. Матрица, обратная ортогональной, тоже ортогональна.

Но сумма ортогональных матриц не является ортогональной.

Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.

Определение. Ортогональный оператор – это оператор евклидова пространства, матрица которого ортогональна в некотором ортонормированном базисе.

Теорема. Линейный оператор евклидова пространства является ортогональным тогда и только тогда, когда оно переводит ортонормированный базис в ортонормированный.

□ По предыдущей теореме матрица перехода от одного ортонормированного базиса к другому является ортогональной, следовательно, линейный оператор, соответствующий данной матрицы, ортогонален. И обратно, если имеется линейный оператор в некотором ортонормированном базисе с ортогональной матрицей, то из ортогональности следует, что

Где каждый из векторов второго базиса равен ( ), коэффициенты этого разложения составляют k-ый столбец ортогональной матрицы перехода. Отсюда следует ортонормированность базиса . ■

Известно, что ортогональный оператор не меняет скалярного произведения векторов (следует из выражения скалярного произведения через координаты векторов в ортонормированном базисе), а следовательно, не меняется норма вектора и угол между двумя векторами.