
- •Ядро и образ линейного оператора.
- •§ Матрица линейного оператора.
- •Переход к другим базисам.
- •§ Обратный оператор.
- •Характеристическое уравнение и собственный вектор линейного оператора.
- •Свойства собственных векторов и собственных значений.
- •Диагональный вид матриц линейного оператора.
- •Действия над линейными операторами.
- •Ортогональные матрицы.
Свойства собственных векторов и собственных значений.
Собственные значения линейного оператора f (и его матрицы А) не зависит от базиса.
Если матрица имеет собственное значение
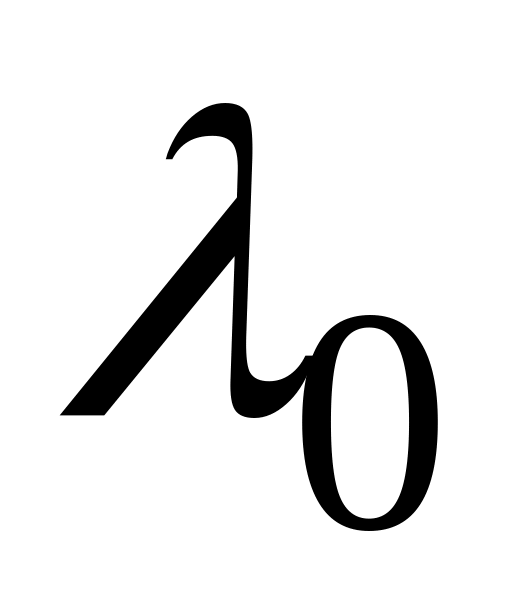 ,
то
,
то
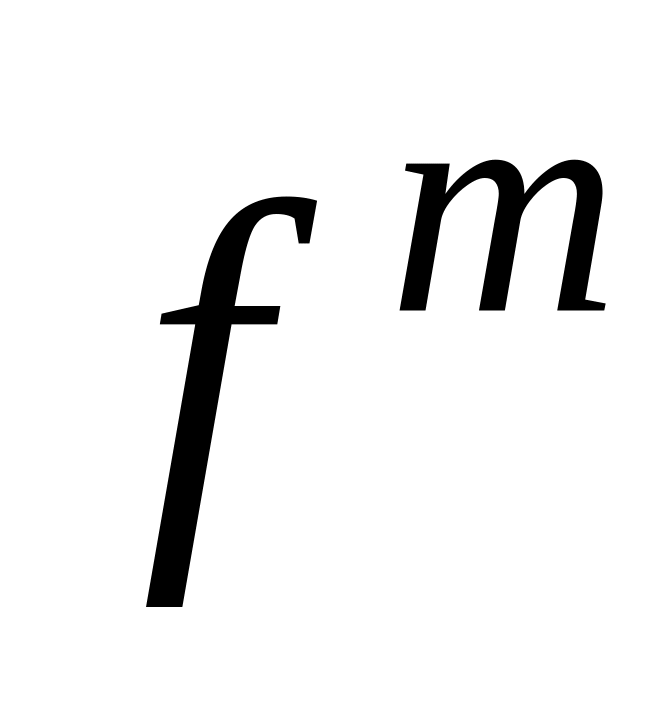 ,
где
,
где
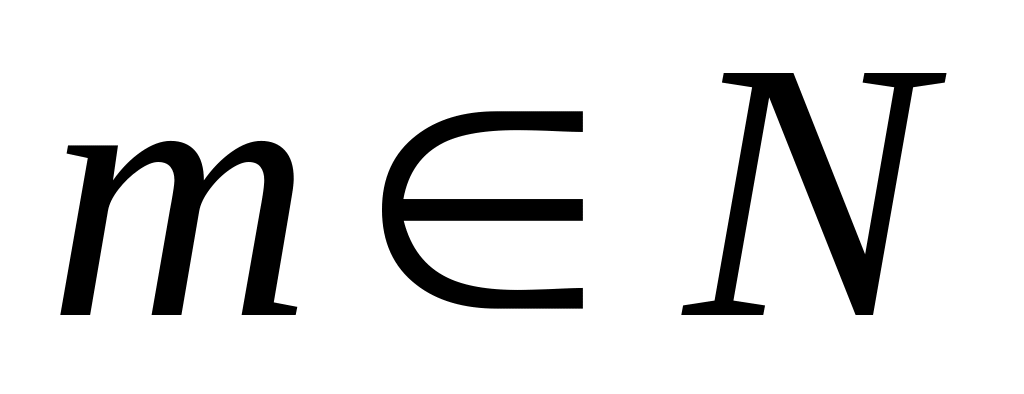 ,
имеет собственное значение
,
имеет собственное значение
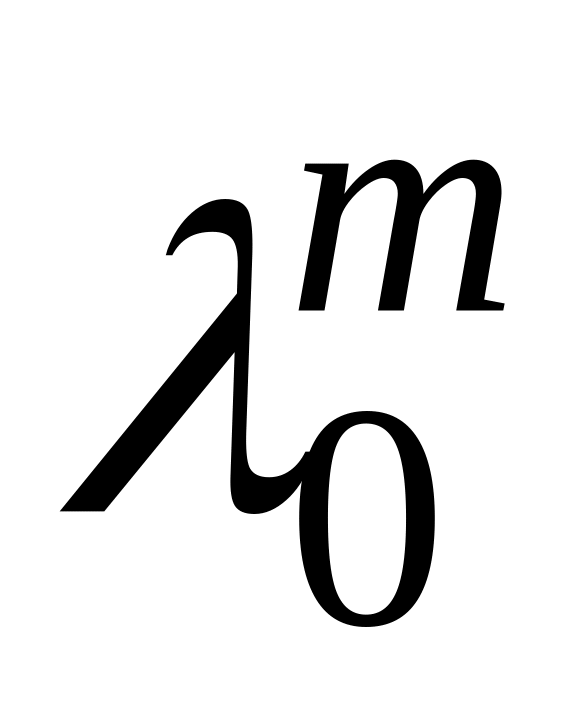 ,
для невырожденных матриц утверждение
верно и для целых m.
,
для невырожденных матриц утверждение
верно и для целых m.Каждому собственному вектору соответствует единственное собственное значение.
Собственные векторы
 ,
отвечающие попарно различным собственным
значениям
,
отвечающие попарно различным собственным
значениям
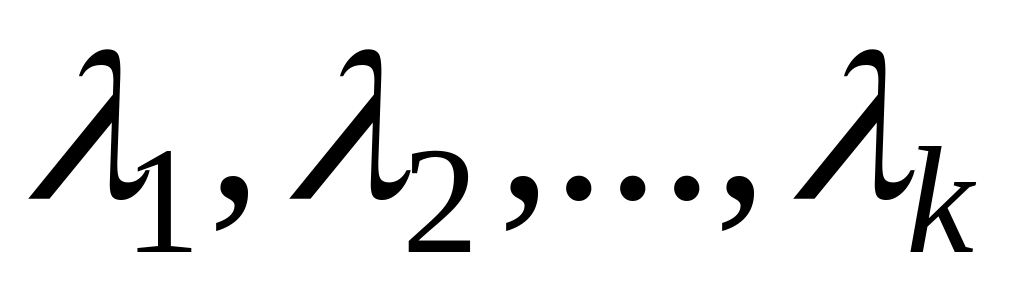
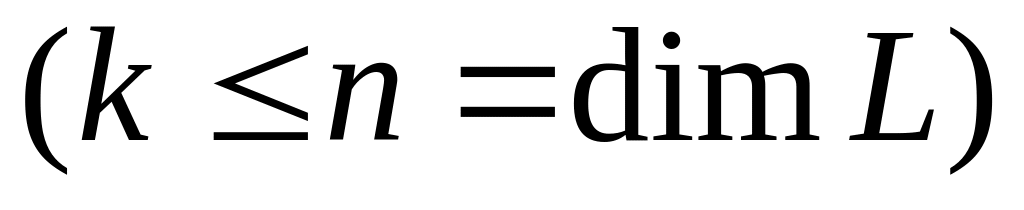 ,
линейно-независимы.
,
линейно-независимы.Если собственному вектору
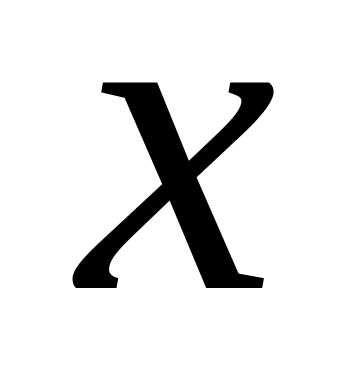 некоторого линейного оператора
соответствует собственное значение
λ, то вектор
некоторого линейного оператора
соответствует собственное значение
λ, то вектор
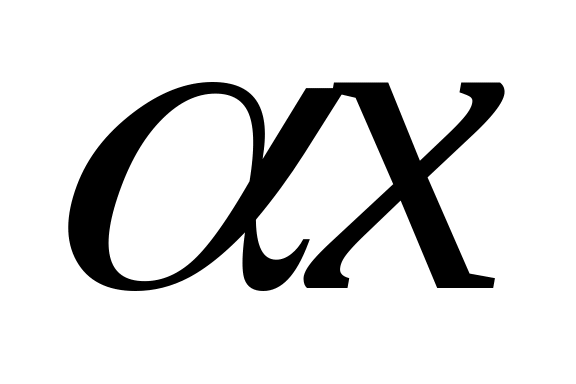 также является собственным вектором
этого же линейного оператора с тем же
собственным значением. Действительно,
так как λ и α числа, то
также является собственным вектором
этого же линейного оператора с тем же
собственным значением. Действительно,
так как λ и α числа, то
 .
.Сумма двух линейно независимых собственных векторов x и y линейного оператора, имеющих одно и то же собственное значение λ, является собственным вектором того же линейного оператора с тем же собственным значением. Действительно, сумма
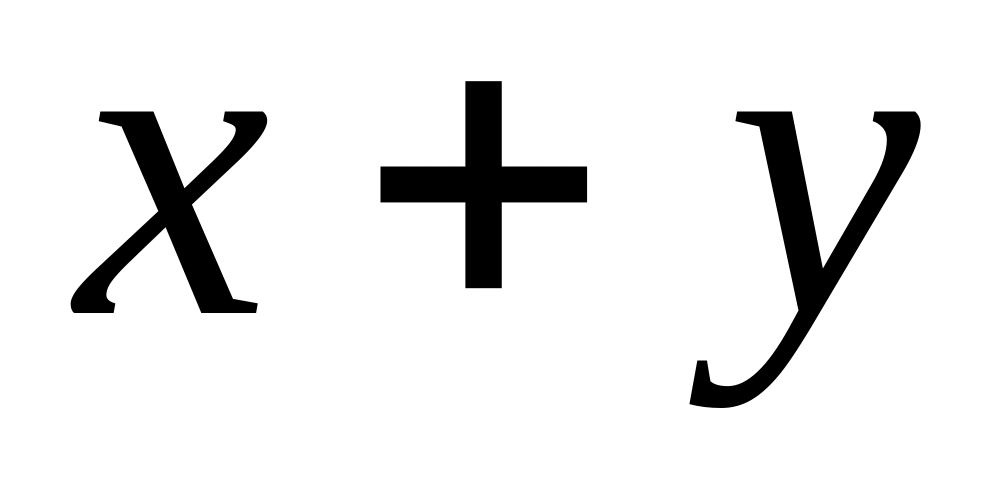 не является нулевым вектором, поскольку
x
и y
линейно независимы, и по свойству
линейного оператора
не является нулевым вектором, поскольку
x
и y
линейно независимы, и по свойству
линейного оператора
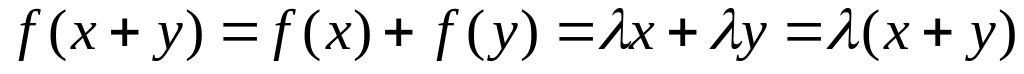 .
.
Если матрица А линейного оператора является симметрической (симметричные относительно главной диагонали элементы равны), то для нее справедливо:
Корни характеристического уравнения являются действительными числами (действительная симметрическая матрица имеет только действительные собственные векторы),
Собственные векторы действительной симметрической матрицы, соответствующие разным собственным значениям, ортогональны.
Матрица А линейного оператора f зависит от выбранного базиса и содержит в себе все свойства оператора А, чем проще устроена матрица, тем легче выявить свойства оператора. Самыми простыми являются диагональные матрицы.
Диагональный вид матриц линейного оператора.
Пусть имеется некоторый линейный оператор с матрицей А.
Теорема (условие диагональности матрицы). Матрица линейного оператора имеет диагональный вид тогда и только тогда, когда каждый базисный вектор является собственным вектором этого оператора.
□ если матрица линейного оператора имеет диагональный вид
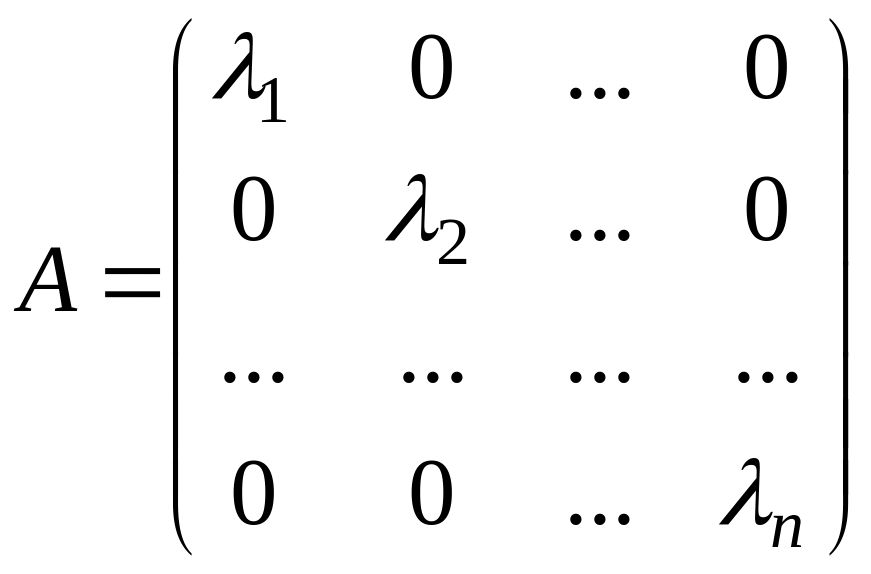 ,
,
то
векторы соответствующего базиса
![]() могут
быть представлены в виде
могут
быть представлены в виде
![]() ,
что означает, что они являются собственными
векторами. И обратно, если векторы базиса
являются собственными, т. е. имеет место
равенство
,
то матрица А имеет диагональный вид. ■
,
что означает, что они являются собственными
векторами. И обратно, если векторы базиса
являются собственными, т. е. имеет место
равенство
,
то матрица А имеет диагональный вид. ■
Определение.
Приводимой
к диагональному виду
называется такая матрица А, для которой
существует невырожденная матрица Т,
для которой матрица
![]() является диагональной. Чтобы построить
матрицу Т, надо определить собственные
числа
является диагональной. Чтобы построить
матрицу Т, надо определить собственные
числа
![]() из характеристического уравнения для
матрицы А.
из характеристического уравнения для
матрицы А.
Теорема. Матрица А линейного оператора f n-мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис этого пространства, состоящий из собственных векторов данного оператора.
Доказательство основывается на предыдущей теореме и определении.
Матрица будет приводиться к диагональному виду, если все ее собственные числа попарно различны.
