3. Боковая аэродинамическая сила. Коэффициент боковой аэродинамической силы. Угол скольжения.

Боковая сила возникает в результате воздействия по­тока на боковую поверхность фюзеляжа и вертикальное оперение при движении самолета.

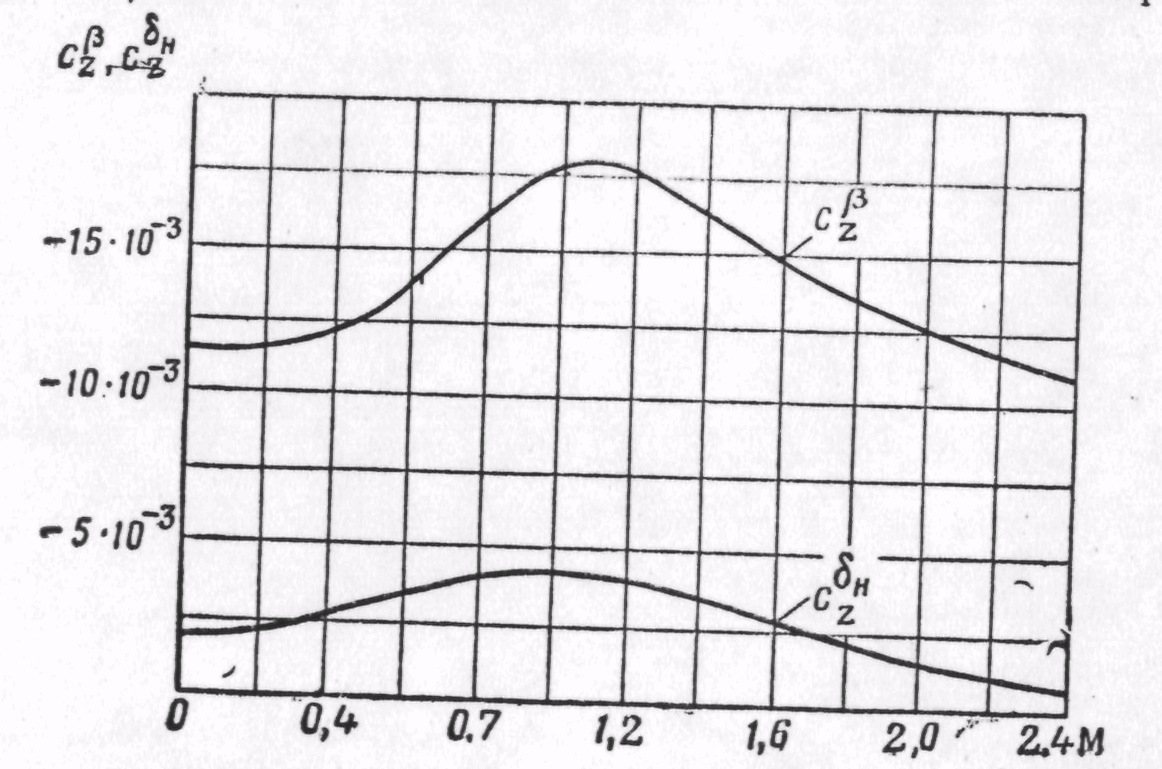
Рис. 19. Зависимость коэффициентов и от числа М

Эта сила возникает при скольжении самолета и отклонении руля направле­ния. Коэффициент боковой силы зависит от угла сколь­жения и угла отклонения руля направления . Угол скольжения — это угол между вектором скорости и плоскостью симметрии са­молета.

В первом приближении коэффициент боковой силы определяется выражением:

(16)

Коэффициенты и — частные производные по углу скольжения и углу отклонения руля направления — всегда отрицательны и изменяются в зависимости от числа М полета (рис. 19).

Коэффициент боковой силы является функцией двух переменных, или аргументов, и Частной произ­водной функции нескольких аргументов называется производная по одному из аргументов предположе­нии, что другие аргументы остаются постоянными ( = const).

Величина боковой силы определяется по формуле:

(17)

ЛЕКЦИЯ 3. АЕРОДИНАМИЧЕСКИЕ МОМЕНТЫ И ИХ КОЭФФИЦИЕНТЫ

1.	Аэродинамические ЛА-центрические прямо-угольные системы координат.
2.	Схема моментов действующих на летательный аппарат в связанной системе координат.
3.	Система продольных моментов действующих на летательный аппарат в полете.
4.	Система поперечных моментов действующих на летательный аппарат в полете.
5.	Система боковых моментов действующих на летательный аппарат в полете.

1. Аэродинамические ла - центрические прямоугольные системы координат

Движение самолета описывает­ся дифференциальными уравнениями, которые отражают характер изменения сил и моментов, действующих на самолет. Параметры движения самолета (скорость, вы­сота, угловое положение) измеряются относительно определенных систем отсчета. Поэтому уравнения дви­жения самолета могут быть составлены в некоторой определенной системе координат. Систему координат выбирают таким образом, чтобы записываемые в ней уравнения движения имели простой и удобный для моделирования вид. На практике применяются четыре прямоугольных системы координат: земная, связанная, скоростная, полу­связанная.

Земная система координат (рис. 1) непо­движно связана с Землей. Начало координат при моделировании полета самолета обычно помещается в точке старта (начало ВПП). Ось направляется вер­тикально вверх, ось — горизонтально в направлении на север.

Ось направляется перпендикулярно плоско­сти так, чтобы система координат была правой.

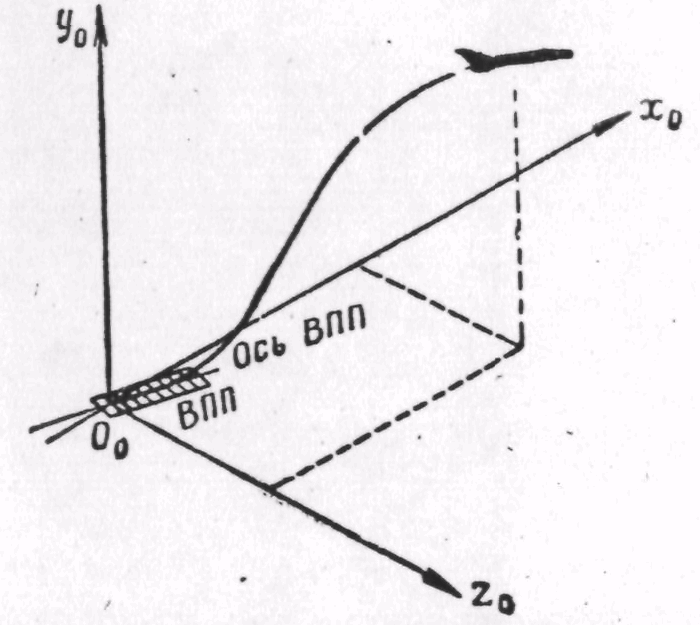
Рис. 1. Земная система координат

Связанная система координат (рис. 2) же­стко связана с самолетом. Оси и располагают­ся в плоскости симметрии. Ось направляется впе­ред по продольной оси самолета, а ось совпадает с нормальной осью, т. е. перпендикулярна оси . Ось перпендикулярна плоскости симметрии и направлена в сторону правого крыла.

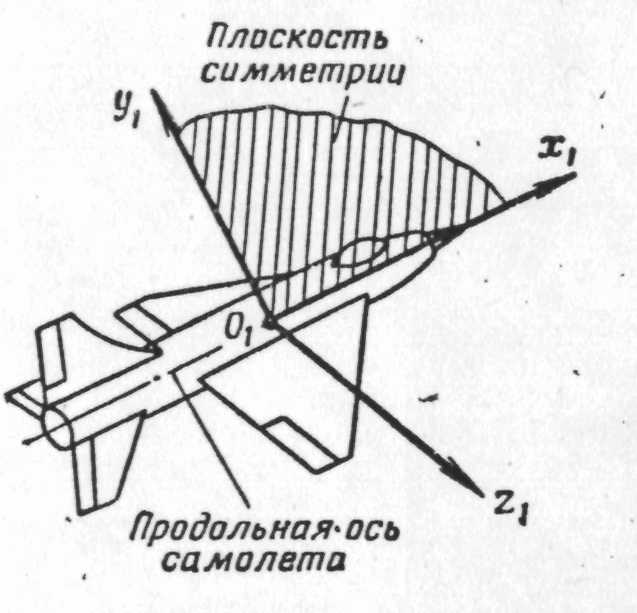
Рис. 2. Связанная система координат

Скоростная, или поточная, система координат (рис. 3) связана с вектором воздушной скорости само­лета V. Ось Ох направлена по вектору скорости V. Оси Оу и лежат в плоскости, перпендикулярной век­тору скорости, ось Оу располагается в плоскости сим­метрии самолета, а ось направляется в сторону пра­вого крыла.

Полусвязанная система координат (рис. 4) отличается от скоростной тем, что ось направляется по проекции вектора скорости V на плоскость симметрии самолета. Ось совпадает со скоростной осью Оу, а ось — со связанной осью

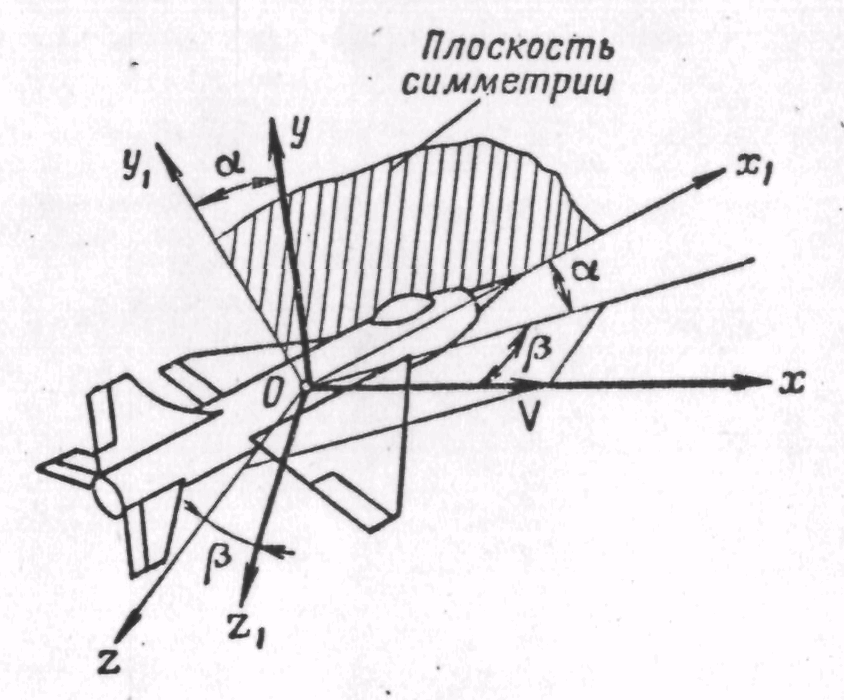
Рис. 3. Скоростная система координат

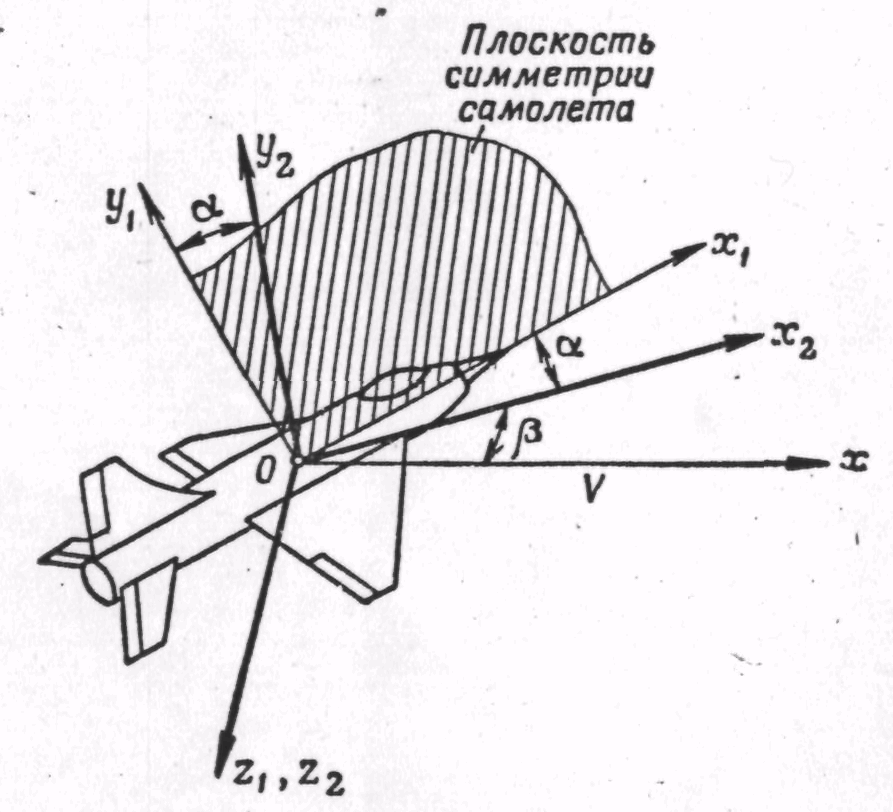
Рис. 4. Полусвязанная система

Положение летательного аппарата относительно зем­ной системы координат определяется шестью координа­тами:

- тремя координатами начала координат связанной системы осей;

- тремя углами между связанной и земной системами координат.

Угол крена (рис. 5) представляет собой угол, образуемый плоскостью симметрии самолета с верти­кальной плоскостью, проходящей через ось .

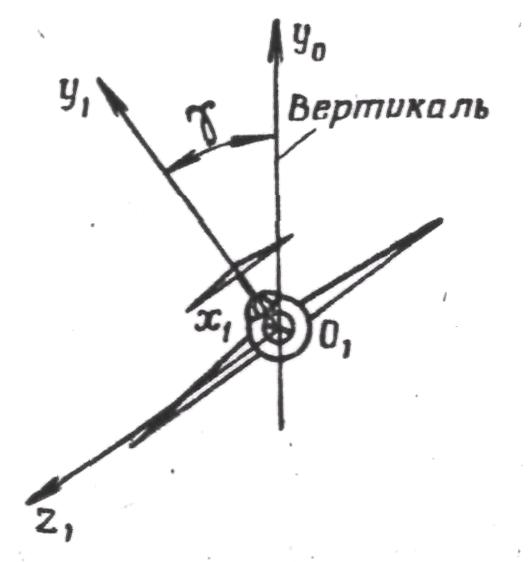
Рис. 5. Угол крена самолета

Угол рыскания (рис. 6) — это угол между проек­цией продольной оси на горизонтальную плоскость и земной осью .

Углом тангажа (рис. 7) называется угол между продольной осью и горизонтальной плоскостью.

Центр тяжести самолета при полете перемещается по некоторой траектории. Вектор скорости полета в лю­бой точке направлен по касательной к траектории. По­ложение вектора воздушной скорости V относительно самолета определяется углами атаки и скольжения .

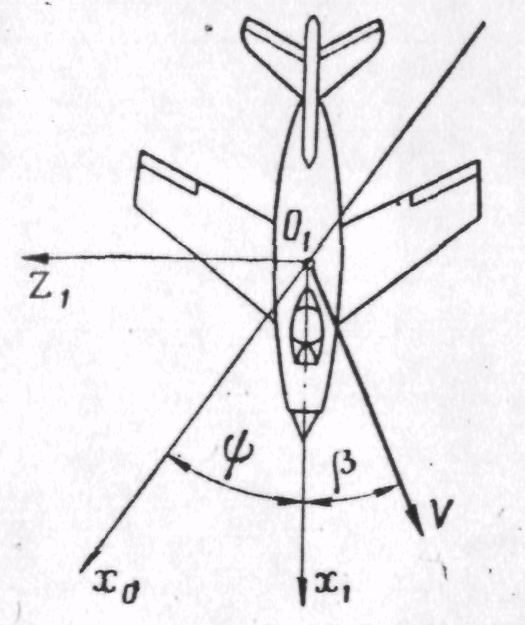
Рис. 6. Углы рыскания и скольжения

Углом атаки называется угол между проекцией вектора скорости V на плоскость симметрии и продоль­ной осью самолета . Угол скольжения — это угол между вектором скорости и плоскостью симметрии са­молета.

Направление вектора скорости в земной системе опре­деляется углами и . Угол наклона траектории в вертикальной плоскости (рис. 7) — это угол между век­тором скорости V и горизонтальной плоскостью. Угол траектории измеряется углом между проекцией век­тора скорости V на горизонтальную плоскость и осью земной системы координат.

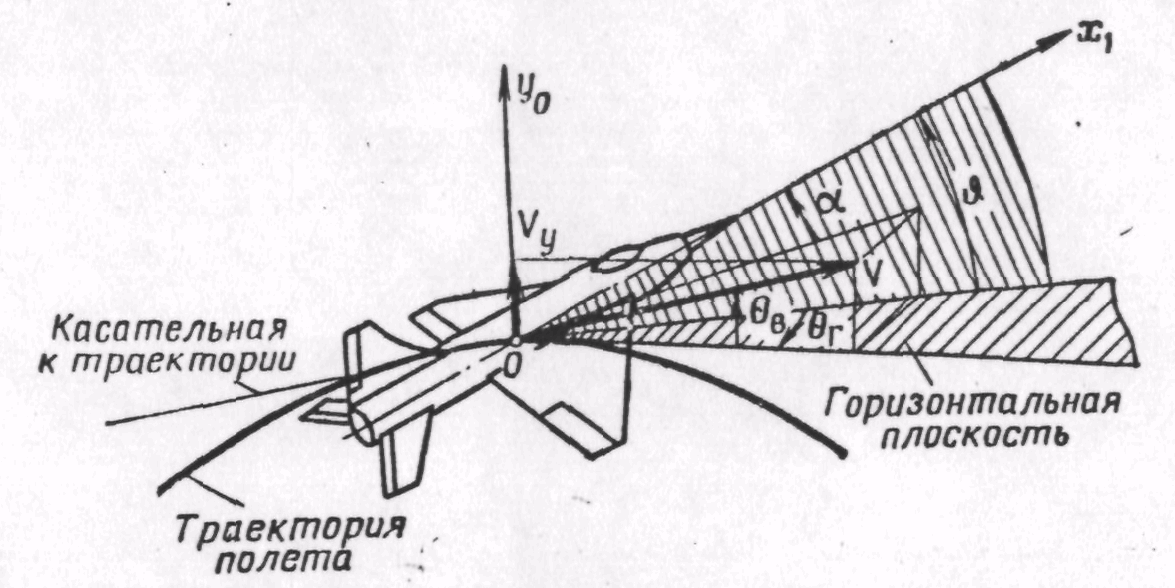
Рис. 7. Углы тангажа, атаки и наклона траектории

Знаки углов определяются следую­щими правилами:

- угол крена положителен при крене самолета вправо;

- угол рыскания имеет знак «+», если проекция продольной оси самолета на горизонтальную пло­скость повернута влево от земной оси _;

- угол тангажа положителен, когда продольная ось самолета направлена вверх от горизонтальной плоскости, проходящей через его центр тяжести;

- угол атаки положителен, если вектор скоро­сти V направлен вниз от продольной оси самолета;

- угол скольжения имеет знак «+», если вектор скорости V находится справа от плоскости симметрии самолета;

- угол наклона траектории положителен, если вектор скорости V направлен вверх от горизонтальной плоскости, проходящей через центр тяжести само­лета;

- угол имеет знак «+», когда проекция вектора скорости на горизонтальную плоскость направлена впра­во от оси земной системы координат.