1.2.1 Построение планов положений механизма
Для
выполнения этого пункта необходимо
знать размеры звеньев:
м;
м.
Определим
масштабный коэффициент
длин:
,
где
– отрезок на чертеже, которым изображается
кривошип. Определим
масштабную длину других звеньев:
,
где
– отрезок на чертеже;
–
заданная длина
шатуна.
Таблица 1.1 – Звенья и кинематические пары механизма гидравлического насоса
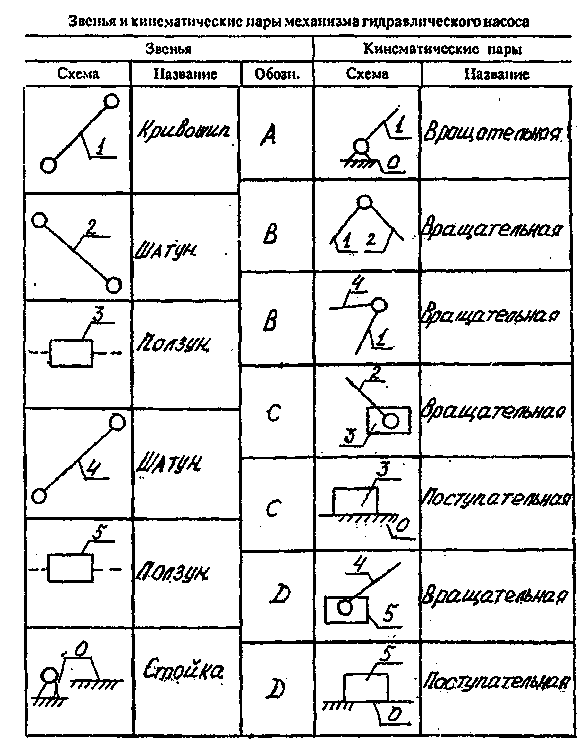
В принятом масштабе выполняем схему механизма в 12 положениях.
По
построенным планам положений можно
определить траектории движения
точек механизма. Ход ползуна:
.
Одно из положений (в данном случае 3-е) обводится основной линией, остальные – тонкими (вспомогательными).
1.2.2 Построение планов скоростей
Планом скоростей называется такое графическое изображение, при котором векторы абсолютных скоростей выходят из одной точки, называемой полюсом. Построение плана рассмотрим на примере 3-го положения механизма.
Определим
скорость точки
.
Поскольку она совершает вращательное
движение относительно центра
с постоянной угловой скоростью
рад/с,
.
Выберем масштаб построения:
.
Из
произвольно выбранного полюса
проводим вектор
длиной 50
мм перпендикулярно звену
по направлению вращения кривошипа.
Для
определения скорости точки
составим два векторных
уравнения:
где
-
вектор скорости неподвижной точки
,
принадлежащей
стойке
- векторы скоростей точки
относительно точек
и
- Вектор
является
линейной скоростью вращательного
движения
шатуна относительно точки
.
Следовательно, он перпендикулярен
звену
.
Вектор
характеризует
поступательное движение
ползуна 3.
Систему уравнений решим графически.
Скорость точки равна:
Величину угловой скорости шатуна определим по формуле:
Для определения направления угловой скорости ω2 мысленно переносим вектор относительной скорости VCВ в точку С механизма; его направление укажет направление вращения шатуна.
Построим 12 планов скоростей для каждого положения механизма. Вычислим линейную скорость точки С и угловую скорость ω2 для каждого из них, пользуясь приведёнными выше формулами.
Таблица 1.2 – Линейные и угловые скорости точек и звеньев механизма
Параметр |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Pc,мм |
5,67 |
30 |
42,57 |
40 |
26,65 |
10,2 |
5,67 |
30 |
42,57 |
40 |
26,65 |
10,2 |
Vc, м/с |
0,16 |
0,83 |
1,17 |
1,1 |
0,73 |
0,28 |
0,16 |
0,83 |
1,17 |
1,1 |
0,73 |
0,28 |
BC,мм |
40 |
36 |
21,5 |
0 |
21,5 |
36 |
40 |
36 |
21,5 |
0 |
21,5 |
36 |
|
2,62 |
2,36 |
1,41 |
0 |
1,41 |
2,36 |
2,62 |
2,36 |
1,41 |
0 |
1,41 |
2,36 |
ω2
,рад/с2