Задание № 1

На рисунке изображена схема энергетических уровней атома водорода. Показаны состояния с различными значениями орбитального квантового числа. Серию Бальмера дают переходы …

Укажите не менее двух вариантов ответа

Задание № 2

Если  -функция электрона в одномерном потенциальном ящике шириной L с бесконечно высокими стенками имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке   равна …

Вероятность обнаружить микрочастицу в интервале (a,b) для состояния, характеризуемого определенной  -функцией, равна  . Используя геометрический смысл интеграла, эту вероятность можно найти как отношение площади под кривой зависимости   в интервале (a,b) к площади под кривой во всем интервале существования  , т.е. в интервале (0,L). Кривая зависимости   от   представлена на рисунке где вероятность обнаружить электрон на участке   соответствует доле «закрашенной» площади от всей площади под кривой (см. рис.), т.е.W =  .

Задание № 3

В опыте Дэвиссона и Джермера исследовалась дифракция прошедших ускоряющее напряжение электронов на монокристалле никеля. Если ускоряющее напряжение уменьшить в 2 раза, то длина волны де Бройля электрона …

Варианты ответа:

Начало формы

уменьшится в   раз

увеличится в   раз

уменьшится в 2 раза

увеличится в 2 раза

Конец формы

Задание № 4

Стационарное уравнение Шредингера имеет вид  . Это уравнение записано для …

Стационарное уравнение Шредингера в общем случае имеет вид  , где U – потенциальная энергия микрочастицы. Для одномерного случая 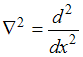 . Кроме того, внутри потенциального ящика  U = 0, а вне ящика частица находиться не может, т.к. его стенки бесконечно высоки. Поэтому данное уравнение Шредингера записано для частицы в одномерном ящике с бесконечно высокими стенками

Конец формы

Задание № 5

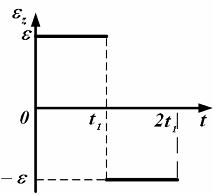
Твердое тело начинает вращаться вокруг оси z. Зависимость углового ускорения   от  времени t  представлена на графике.  Соответствующая зависимость угловой скорости   от времени  представлена графиком …

Угловое ускорение характеризует быстроту изменения угловой скорости тела  . При неизменной оси вращения векторы    и    совпадают по направлению,  если   (угловая скорость возрастает) и направлены противоположно, если    (скорость вращения уменьшается).  По условию задания в интервале времени от 0 до   твердое тело начинает вращаться вокруг оси   с постоянным угловым ускорением  , следовательно, в этом интервале времени  угловая скорость   линейно возрастает от 0 до  значения  (см. рис.). В интервале времени от   до    проекция углового ускорения меняет знак,  , значит, угловая скорость в этом интервале будет линейно убывать от значения   до 0 (см. рис.).

Конец формы

Задание № 6

Тело массы   поднимают по наклонной плоскости. Высота наклонной плоскости  , длина ее основания  , коэффициент трения  . Минимальная  работа, которую надо совершить, в джоулях равна  …

Минимальная сила, которую надо приложить к телу, чтобы поднимать его по наклонной плоскости без ускорения, равна сумме составляющей силы тяжести, параллельной наклонной плоскости, и силы трения:  . Работа равна  , где l– длина  наклонной плоскости. Учитывая, что    и  , получим  . Следовательно, минимальная работа  .

Задание № 7

Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью  . Если экспериментатор повернет ось вращения колеса на угол  , то он вместе с платформой придет во вращение с угловой скоростью  . 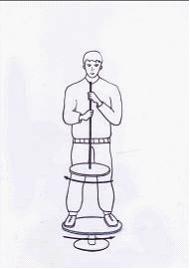Отношение момента инерции экспериментатора со скамьей к моменту инерции колеса равно …

Воспользуемся законом сохранения момента импульса:  . Векторы момента  импульса системы    и   до поворота и после поворота оси вращения колеса равны:   и   , где   и  ,   и   – моменты инерции и векторы угловых скоростей человека со скамьей и колеса соответственно. Следовательно,  , а в проекциях на вертикальную ось:  . Знак минус показывает изменение направления  момента импульса колеса при повороте его оси вращения на угол  . Из последнего уравнения находим отношение момента инерции тела человека вместе со скамьей к моменту инерции колеса: .

Задание № 8

Обруч, раскрученный в вертикальной плоскости и посланный по полу рукой гимнастки, через несколько секунд сам возвращается к ней. Начальная скорость центра обруча равна  , коэффициент трения между обручем и полом равен  . Расстояние, на которое откатывается обруч, в   равно …

В горизонтальном направлении на обруч действует только сила трения   , где   - коэффициент трения. Согласно теореме о движении центра масс, центр обруча движется, как материальная точка с массой  , равной массе обруча, к которой приложена сила трения. Ускорение торможения равно  , время торможения  , пройденное до остановки расстояние  .

Задание № 9

Скорость частицы  , где c – скорость света. Отношение полной энергии частицы к ее энергии покоя равно 

Полная энергия частицы    , энергия покоя   . Отношение  . Подставляя  , получим 

Задание № 10

Величина момента импульса тела относительно неподвижной оси изменяется по закону ;  при этом зависимость величины момента сил, действующих на тело, описывается графиком …

Cкорость изменения величины момента импульса относительно какой-то неподвижной оси равна величине суммарного момента внешних сил относительно этой оси, т.е.    где   – величина момента импульса,   – величина момента силы. Вычислив производную от функции, характеризующей зависимость величины момента импульса от времени, получим зависимость величины момента силы от времени. .  Графиком этой функции является убывающая ветвь параболы.

Задание № 11

При освещении металла излучением с длиной волны    фототок прекращается при задерживающем напряжении  . Если изменить длину волны излучения в 1,5 раза, то задерживающее напряжение увеличится в 2 раза. Работа выхода электронов из металла  . Задерживающее напряжение   в вольтах для излучения с длиной волны   равно …

Запишем уравнение Эйнштейна для фотоэффекта под действием излучения с длиной волны  :   . Изменение длины волны в данном случае означает уменьшение, так как задерживающее напряжение увеличилось. Имеем  . Подставляя   из первого уравнения,  получим  . Отсюда находим   и  .

Задание № 12

Постоянная дифракционной решетки равна 2 мкм. Наибольший порядок спектра для желтой линии натрия  равен …

Запишем формулу дифракционной решетки    и выразимk  Максимальный порядок спектра будет при  ,  . Округляя до ближайшего целого меньшего числа, получим  .

Задание № 13

Графики дисперсионных кривых зависимостей показателя преломления среды от частоты   и длины волны   света имеют вид, представленный на рисунках: Участки кривых   и   соответствуют дисперсии …

Дисперсию света в среде называют нормальной, если с ростом частоты   абсолютный показатель преломления   среды также возрастает ( ) или если с ростом длины волны   абсолютный показатель преломления   уменьшается ( ). Наоборот, если   и соответственно  , то дисперсию света в среде называют аномальной. На участках   и   дисперсионных кривых показатель преломления   возрастает ( ) с ростом частоты   и уменьшается ( ) с ростом длины волны  . Следовательно, оба участка   и   дисперсионных кривых соответствуют нормальной дисперсии.