Содержание

Ведение 2

Глава 1. Итерационные методы решения линейных систем 3

1. Метод простой итерации 3

2. Одношаговый циклический процесс 6

3 .Метод Некрасова 8

4 .Методы полной релаксации 9

5. Неполная релаксация 10

6. Градиентный метод с минимальными невязками 11

7. Градиентные методы с неполной релаксацией 11

Заключение 14

Список используемой литературы 15

Ведение

Современная вычислительная математика располагает большим арсеналом методов, а математическое обеспечение ЭВМ-многими пакетами прикладных программ, позволяющие решать различные возникающие на практике линейные системы. Чтобы ориентироваться среди методов и программ и в нужный момент сделать оптимальный выбор, нужно разбираться в основах построений методов и алгоритмов, учитывая специфику постановок задач, знать их сильные и слабые стороны и границы применимости.

Целями данной курсовой работы являются рассмотрение итерационных методов решения линейных систем

В первой главе рассматриваются итерационные методы: метод простой итерации, одношаговый циклический процесс, метод Некрасова, методы полной релаксации, неполная релаксация, градиентный метод с минимальными невязками, градиентные методы с неполной релаксацией [10], метод Якоби [11].

Глава 1. Итерационные методы решения линейных систем

В этой главе используется материал, кроме метода Якоби, из источника [11].

Метод Якоби взят из источника [10].

1. Метод простой итерации

Условия сходимости метода последовательных приближений тре­буют, чтобы матрица коэффициентов системы была, в том или ином смысле, близка к единичной матрице. Если это условие не выполнено или „плохо выполнено", систему целесообразно пред­варительно подготовить к применению метода последовательных при­ближений. Подготовка состоит в переходе от данной системы к равносильной системе

,

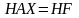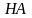где некоторая неособенная матрица, которая выбирается так, чтобы матрица была бы близка к единичной, т. е. матрица была бы близка к .

Применение метода последовательных приближений к подгото­вленной системе равносильно применению стацио­нарного итерационного процесса

к исходной системе.

Выбор матрицы может быть осуществлен с использованием частных особенностей данной системы. Рассмотрим некоторые наибо­лее употребительные способы подготовки, использующие лишь до­вольно поверхностные сведения о матрице коэффициентов.

Пусть матрица положительно определена. Тогда система всегда может быть подготовлена к виду, в котором метод последова­тельных приближений будет сходящимся. Вычислив, например, первую норму µ матрицы , мы получим, что все собственные значения матрицы заключены в открытом интервале (0, µ). Положим

(1.1.1)

Система преобразуется к виду

(1.1.2)

Собственные значения матрицы будут заключены в открытом интервале (-1, 1) и, следовательно, метод последова­тельных приближений будет сходящимся.

В прикладных процессах часто встречаются системы, в которых диагональные элементы матрицы значительно преобладают над остальными элементами матрицы. В этом случае подготовка системы осуществляется так.

Перепишем систему в развернутом виде

(1.1.3)

Поделим каждое уравнение системы (1.1.3)на диагональный элемент.

Получим систему

или в матричной записи

(1.1.4)

где

(1.1.5)

Для применения процесса итерации нет необходимости на самом деле делать преобразование системы (1.1.3) в систему (1.1.4). Последовательные приближения можно вычислять по формулам:

(1.1.6)

Описанная модификация процесса последовательных приближений имеет название метода простой итерации [10].